GAMMA
This function evaluates the complete gamma function.
Function Return Value
GAMMA — Function value. (Output)
Required Arguments
X — Argument for which the complete gamma function is desired. (Input)
FORTRAN 90 Interface
Generic: GAMMA (X)
Specific: The specific interface names are S_GAMMA, D_GAMMA, and C_GAMMA.
FORTRAN 77 Interface
Single: GAMMA (X)
Double: The double precision function name is DGAMMA.
Complex: The complex name is CGAMMA.
Description
The gamma function, Γ(z), is defined to be
For ℜ(z) < 0, the above definition is extended by analytic continuation.
z must not be so close to a negative integer that the result is less accurate than half precision. If ℜ(z) is too small, then the result will underflow. Users who need such values should use the log gamma function ALNGAM. When ℑ(z) ≈ 0, ℜ(z) should be greater than xmin so that the result does not underflow, and ℜ(z) should be less than xmax so that the result does not overflow. xmin and xmax are available by
CALL R9GAML (XMIN, XMAX)
Note that z must not be too far from the real axis because the result will underflow.
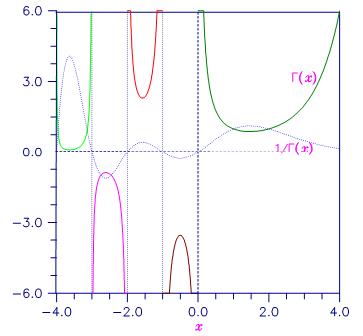
Figure 4, Plot of Γ(x) and 1/Γ(x)
Comments
Informational Errors
Type | Code | Description |
|---|---|---|
2 | 3 | The function underflows because X is too small. |
3 | 2 | Result is accurate to less than one‑half precision because X is too near a negative integer. |
Examples
Example 1
In this example, Γ(5.0) is computed and printed.
USE GAMMA_INT
USE UMACH_INT
IMPLICIT NONE
! Declare variables
INTEGER NOUT
REAL VALUE, X
! Compute
X = 5.0
VALUE = GAMMA(X)
! Print the results
CALL UMACH (2, NOUT)
WRITE (NOUT,99999) X, VALUE
99999 FORMAT (' GAMMA(', F6.3, ') = ', F6.3)
END
Output
GAMMA( 5.000) = 24.000
Example 2
In this example, Γ(1.4 + 3i) is computed and printed.
USE GAMMA_INT
USE UMACH_INT
IMPLICIT NONE
! Declare variables
INTEGER NOUT
COMPLEX VALUE, Z
! Compute
Z = (1.4, 3.0)
VALUE = GAMMA(Z)
! Print the results
CALL UMACH (2, NOUT)
WRITE (NOUT,99999) Z, VALUE
99999 FORMAT (' GAMMA(', F6.3, ',', F6.3, ') = (', &
F6.3, ',', F6.3, ')')
END
Output
GAMMA( 1.400, 3.000) = (-0.001, 0.061)
Published date: 03/19/2020
Last modified date: 03/19/2020