DESKN
Performs nonparametric probability density function estimation by the kernel method.
Required Arguments
XKER — User‑supplied FUNCTION to compute the kernel at any point on the real line. The form is XKER(Y), where:
Y — Point at which the kernel is to be evaluated.
XKER — Value of the kernel at point Y.
X — Vector of length NOBS containing the random sample of observations. (Input)
WINDOW — Window width for the kernel function. (Input)
Generally, several different values of WINDOW should be tried.
Generally, several different values of WINDOW should be tried.
XMAX — Cutoff value such that XKER(Y) = 0.0 for all ∣Y∣ greater than XMAX. (Input)
If XMAX exists, then the kernel function is 0.0 for all Y greater in absolute value than XMAX, and the efficiency of the computations is enhanced. If no such XMAX exists or the user does not wish to make use of XMAX, then XMAX should be assigned any nonpositive value.
If XMAX exists, then the kernel function is 0.0 for all Y greater in absolute value than XMAX, and the efficiency of the computations is enhanced. If no such XMAX exists or the user does not wish to make use of XMAX, then XMAX should be assigned any nonpositive value.
XPT — Vector of length NXPT containing the values at which a density estimate is desired. (Input)
If XMAX is greater than zero, then XPT must be sorted from smallest to largest.
If XMAX is greater than zero, then XPT must be sorted from smallest to largest.
DENS — Vector of length NXPT containing the density estimates at the points specified in XPT. (Output)
Optional Arguments
NOBS — Number of observations. (Input)
Default: NOBS = size (X,1).
Default: NOBS = size (X,1).
NXPT — Number of points at which a density estimate is desired. (Input)
Default: NXPT = size (XPT,1).
Default: NXPT = size (XPT,1).
NMISS — Number of missing (NaN, not a number) values in X. (Output)
FORTRAN 90 Interface
Generic: CALL DESKN (XKER, X, WINDOW, XMAX, XPT, DENS [, …])
Specific: The specific interface names are S_DESKN and D_DESKN.
FORTRAN 77 Interface
Single: CALL DESKN (XKER, NOBS, X, WINDOW, XMAX, NXPT, XPT, DENS, NMISS)
Double: The double precision name is DDESKN.
Description
Routine DESKN computes kernel estimates of the density function for a random sample of (scalar‑valued) observations. The kernel estimate of the density at the point y is given by.
where
is the estimated density at y, K is the kernel function, xi denotes the i‑th observation, n is the number of observations, and h is a fixed constant (called the “window width”) supplied by the user.
One is usually interested in computing the density estimates using several values of the window width h. Tapia and Thompson (1978), Chapter 2, give some considerations relevant to the choice of h. Some common kernel functions (see Tapia and Thompson 1978, page 60) are given as follows.
Name | Function |
|---|---|
Uniform | |
Triangular | |
Biweight | |
Normal |
The computation can be made much more efficient when the kernel is nonzero over a finite range since observations outside this range can be ignored in the computation of the density. In this case, the array XPT is assumed to be sorted.
Comments
1. Informational error
Type | Code | Description |
|---|---|---|
4 | 7 | Negative kernel functions are not allowed. |
2. Routine may be used to obtain interpolated density estimates from the NXPT density estimates returned in DENS. Array AMESH in DESPT corresponds to array XPT in DESKN.
Example
In this example, the standard normal density function is estimated at 13 points using a random sample of 10 points from a standard normal distribution. The biweight kernel function is used. The actual density for the standard normal density is also reported in the output for comparison. The random sample is generated using routines RNSET and RNNOR in Chapter 18, “Random Number Generation”.
USE RNSET_INT
USE RNNOR_INT
USE DESKN_INT
USE UMACH_INT
IMPLICIT NONE
INTEGER NOBS, NXPT
REAL C1, WINDOW, XMAX
PARAMETER (C1=0.3989423, NOBS=10, NXPT=13, WINDOW=2.0, XMAX=1.0)
!
INTEGER I, NMISS, NOUT
REAL DENS(NXPT), EXP, X(NOBS), XKER, XPT(NXPT)
INTRINSIC EXP
EXTERNAL XKER
!
DATA XPT/-3.0, -2.5, -2.0, -1.5, -1.0, -0.5, 0.0, 0.5, 1.0, 1.5, &
2.0, 2.5, 3.0/
!
CALL RNSET (1234457)
CALL RNNOR (X)
CALL DESKN (XKER, X, WINDOW, XMAX, XPT, DENS, NMISS=NMISS)
!
CALL UMACH (2, NOUT)
WRITE (NOUT,'('' NMISS = '', I1)') NMISS
WRITE (NOUT,'('' DENS Estimate = '', 10F6.4,/,8X,3F6.4)') DENS
WRITE (NOUT,'('' DENS Exact = '',10F6.4,/,8X,3F6.4)') &
(C1*EXP(-XPT(I)*XPT(I)/2.0),I=1,NXPT)
END
REAL FUNCTION XKER (Y)
REAL Y
!
REAL ABS
INTRINSIC ABS
!
IF (ABS(Y) .LT. 1.0) THEN
XKER = 15.0*(1.0-Y*Y)*(1.0-Y*Y)/16.0
ELSE
XKER = 0.0
END IF
RETURN
END
Output
NMISS = 0
DENS Estimate = 0.00000.01180.07900.16980.26780.34670.36870.31840.22340.1391
0.06120.01350.0005
DENS Exact = 0.00440.01750.05400.12950.24200.35210.39890.35210.24200.1295
0.05400.01750.0044
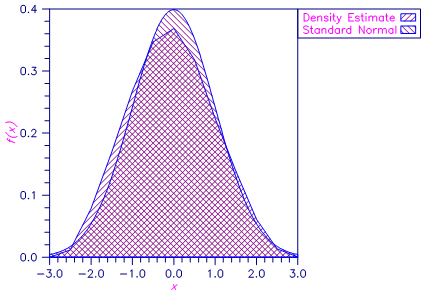
Figure 21, Density Estimate and Standard Normal Density
Published date: 03/19/2020
Last modified date: 03/19/2020