BETDF
This function evaluates the beta cumulative distribution function.
Function Return Value
BETDF — Probability that a random variable from a beta distribution having parameters PIN and QIN will be less than or equal to X. (Output)
Required Arguments
X — Argument for which the beta distribution function is to be evaluated. (Input)
PIN — First beta distribution parameter. (Input)
PIN must be positive.
PIN must be positive.
QIN — Second beta distribution parameter. (Input)
QIN must be positive.
QIN must be positive.
FORTRAN 90 Interface
Generic: BETDF (X, PIN, QIN)
Specific: The specific interface names are S_BETDF and D_BETDF.
FORTRAN 77 Interface
Single: BETDF (X, PIN, QIN)
Double: The double precision name is DBETDF.
Description
Function BETDF evaluates the cumulative distribution function of a beta random variable with parameters PIN and QIN. This function is sometimes called the incomplete beta ratio and, with p = PIN and q = QIN, is denoted by Ix(p, q). It is given by
where Γ(⋅) is the gamma function. The value of the distribution function Ix(p, q) is the probability that the random variable takes a value less than or equal to x.
The integral in the expression above is called the incomplete beta function and is denoted by βx(p, q). The constant in the expression is the reciprocal of the beta function (the incomplete function evaluated at one) and is denoted by β(p, q).
Function BETDF uses the method of Bosten and Battiste (1974).
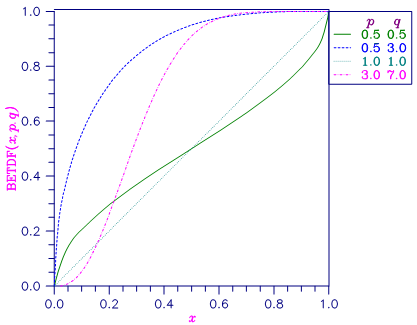
Figure 28, Beta Distribution Function
Comments
Informational Errors
Type | Code | Description |
|---|---|---|
1 | 1 | Since the input argument X is less than or equal to zero, the distribution function is equal to zero at X. |
1 | 2 | Since the input argument X is greater than or equal to one, the distribution function is equal to one at X. |
Example
Suppose X is a beta random variable with parameters 12 and 12. (X has a symmetric distribution.) In this example, we find the probability that X is less than 0.6 and the probability that X is between 0.5 and 0.6. (Since X is a symmetric beta random variable, the probability that it is less than 0.5 is 0.5.)
USE UMACH_INT
USE BETDF_INT
IMPLICIT NONE
INTEGER NOUT
REAL P, PIN, QIN, X
!
CALL UMACH (2, NOUT)
PIN = 12.0
QIN = 12.0
X = 0.6
P = BETDF(X,PIN,QIN)
WRITE (NOUT,99998) P
99998 FORMAT (' The probability that X is less than 0.6 is ', F6.4)
X = 0.5
P = P - BETDF(X,PIN,QIN)
WRITE (NOUT,99999) P
99999 FORMAT (' The probability that X is between 0.5 and 0.6 is ', &
F6.4)
END
Output
The probability that X is less than 0.6 is 0.8364
The probability that X is between 0.5 and 0.6 is 0.3364
Published date: 03/19/2020
Last modified date: 03/19/2020