CTPAR
Computes model estimates and covariances in a fitted log‑linear model.
Required Arguments
NCLVAL — Vector of length NCLVAR containing, in its i‑th element, the number of levels or categories of the i‑th classification variable. (Input)
NVEF — Vector of length NEF containing the number of classification variables associated with each effect. (Input)
INDEF — Vector of length NVEF(1) + … + NVEF(NEF) containing, in consecutive positions, the indices of the variables that are included in each effect. (Input)
The entries in INDEF are sequenced so that the first NVEF(1) elements contain the indices of the variables in effect 1, the next NVEF(2) elements of INDEF contain the indices of the variables in effect 2, etc. See Comment 4 for an example.
The entries in INDEF are sequenced so that the first NVEF(1) elements contain the indices of the variables in effect 1, the next NVEF(2) elements of INDEF contain the indices of the variables in effect 2, etc. See Comment 4 for an example.
FIT — Vector of length NCLVAL(1) * NCLVAL(2) * … * NCLVAL(NCLVAR) containing the model estimates of the cell counts. (Input)
See Comment 3 for the ordering of the elements of FIT. To obtain a first iteration approximation to the optimal parameter values, the observed counts may be input in FIT, in which case a least‑squares model is fit. In all cases, values of zero in FIT are assumed to correspond to structural zeros in the table. See the Description section for details.
See Comment 3 for the ordering of the elements of FIT. To obtain a first iteration approximation to the optimal parameter values, the observed counts may be input in FIT, in which case a least‑squares model is fit. In all cases, values of zero in FIT are assumed to correspond to structural zeros in the table. See the Description section for details.
NCOEF — Number of regression coefficients in the model. (Output)
COEF — NCOEF by 4 matrix containing the estimated coefficients and associated statistics. (Output)
Col. | Statistic |
|---|---|
1 | Coefficient estimate |
2 | Estimated standard error of the estimated coefficient |
3 | Asymptotic normal score for testing that the coefficient is zero |
4 | p‑value associated with the normal score in column 3 (two‑sided alternative) |
COV — NCOEF by NCOEF covariance matrix of the estimated coefficients. (Output)
Optional Arguments
NCLVAR — Number of classification variables. (Input)
A variable specifying a margin in the table is a classification variable. The first classification variable is named A, the second classification variable is named B, etc.
Default: NCLVAR = size (NCLVAL,1).
A variable specifying a margin in the table is a classification variable. The first classification variable is named A, the second classification variable is named B, etc.
Default: NCLVAR = size (NCLVAL,1).
NEF — Number of effects in the model. (Input)
A marginal table is implied by each effect in the model. Lower‑order effects should not be included since their inclusion is automatic in the hierarchical models fit here (e.g., do not include effects A or B if effect AB is in the model).
Default: NEF = size (NVEF,1).
A marginal table is implied by each effect in the model. Lower‑order effects should not be included since their inclusion is automatic in the hierarchical models fit here (e.g., do not include effects A or B if effect AB is in the model).
Default: NEF = size (NVEF,1).
TOL — Tolerance used in determining linear dependence in COV. (Input)
TOL = 100.0 * AMACH(4) is a common choice. See the documentation for routine AMACH in Reference Material.
Default: TOL = 1.19e‑5 for single precision and 2.d –14 for double precision.
TOL = 100.0 * AMACH(4) is a common choice. See the documentation for routine AMACH in Reference Material.
Default: TOL = 1.19e‑5 for single precision and 2.d –14 for double precision.
IPRINT — Printing option. (Input)
Default: IPRINT = 0.
Default: IPRINT = 0.
IPRINT | Action |
|---|---|
0 | No printing is performed. |
1 | Printing of COEF and COV is performed. |
2 | COEF, COV, and FIT are printed. |
In the printing, A * B(2) denotes the second variable in the AB interaction effect.
LDCOEF — Leading dimension of COEF exactly as specified in the dimension statement in the calling program. (Input)
Default: LDCOEF = size (COEF,1).
Default: LDCOEF = size (COEF,1).
LDCOV — Leading dimension of COV exactly as specified in the dimension statement in the calling program. (Input)
Default: LDCOV = size (COV,1).
Default: LDCOV = size (COV,1).
FORTRAN 90 Interface
Generic: CALL CTPAR (NCLVAL, NVEF, INDEF, FIT, NCOEF, COEF, COV [, …])
Specific: The specific interface names are S_CTPAR and D_CTPAR.
FORTRAN 77 Interface
Single: CALL CTPAR (NCLVAR, NCLVAL, NEF, NVEF, INDEF, FIT, TOL, IPRINT, NCOEF, COEF, LDCOEF, COV, LDCOV)
Double: The double precision name is DCTPAR.
Description
Routine CTPAR computes estimates of parameters and associated variances and covariances in hierarchical loglinear models. A weighted least‑squares algorithm is used.
A hierarchical analysis of variance model is a factorial analysis of variance model in which a lower‑order effect is included in a model whenever a higher‑order effect containing it is in the model. Thus, if the effect ADF is in the model, then effects A, D, F, AD, AF, and DF are automatically in the model.
Input to CTPAR may be either the expected table values for the given hierarchical model as output, for example, by routine PRPFT, or the observed table values. When the fitted values are input, the estimates computed are the maximum likelihood estimates. When observed values are input, weighted least‑squares estimates of the parameters in the log‑linear model are computed. (Least‑squares estimates and maximum likelihood estimates can also be computed via routines CTWLS and CTGLM, respectively.)
When an expected count (as input in FIT) is zero, the cell is taken to be a structural zero. Such cells are not included in the weighted least‑squares analysis. Estimates corresponding to structural zeros are set to the missing value indicator (NaN). To avoid this (and to determine the total degrees of freedom for each effect), add a positive constant such as 0.5 to each of the observed cell counts of zero, the “sampling” zeros. When structural zeros are present in the data the estimates may be written as
where
are vectors, and ρ → ∞. Routine CTPAR estimates the finite portion of the estimate,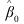 
The infinite portion, 
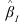ensures that the fitted values for cells corresponding to structural zeros are zero (sampling zeros are considered to be structural zeros in CTPAR). If there are no structural zeros
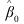The infinite portion, 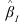ensures that the fitted values for cells corresponding to structural zeros are zero (sampling zeros are considered to be structural zeros in CTPAR). If there are no structural zerosLet fi denote the i‑th element of the vector FIT. The asymptotic variance‑covariance matrix of the cell counts is estimated by a diagonal matrix S = diag(f) where diag(f) denotes the diagonal matrix in which sij = 0 for i ≠ j and sii = fi along the diagonal. If X denotes the design matrix for the hierarchical model (with rows in X corresponding to structural zeros omitted), and yi = logfi, then the weighted least‑squares estimates are
and the estimated variance‑covariance matrix is
(XT S−1X)−1
(see Grizzle, Starmer, and Koch [1969]).
If main effect A has, for example, four levels, then the design matrix X contains three dummy variables corresponding to this effect. Main effect dummy variables are generated as follows: For an observation fi corresponding to level j of the effect, if j < 3, then the j‑th dummy variable is set to 1 with the remaining dummy variables set to 0. If j = 4, then all three dummy variables are set to ‑1. Dummy variables for interactions are generated as the product of the corresponding dummy variables in the usual manner with the smallest index in the specification of the interaction varying fastest. The indices of the classification variables for each effect are always sorted from smallest to largest when computing the columns of X.
Comments
1. Workspace may be explicitly provided, if desired, by use of C2PAR/DC2PAR. The reference is:
CALL C2PAR (NCLVAR, NCLVAL, NEF, NVEF, INDEF, FIT, TOL, IPRINT, NCOEF, COEF, LDCOEF, COV, LDCOV, IRANK, NCVEF, IXEF, IINDEF, IA, INDCL, CLVAL, REG, X, D, XMIN, XMAX, WK)
The additional arguments are as follows:
IRANK — Rank of COV.
NCVEF — Vector of length 2NCLVAR ‑ 1.
IXEF — Vector of length NCLVAR * 2NCLVAR−1.
IINDEF — Vector of length NVEF(1) + … + NVEF(NEF).
IA — Vector of length NCLVAR.
INDCL — Vector of length NCLVAR.
CLVAL — Vector of length NCLVAL(1) + … + NCLVAL(NCLVAR).
REG — Vector of length NCOEF + 1.
X — Vector of length NCLVAR.
D — Vector of length NCOEF.
XMIN — Vector of length NCOEF.
XMAX — Vector of length NCOEF.
WK — Vector of length NCOEF + 1 if IPRINT ≠ 2. Otherwise, its length is the maximum of NCOEF + 1 and the product of the two largest elements of NCLVAL.
2. Informational errors
Type | Code | Description |
|---|---|---|
3 | 5 | The label for one or more of the tables exceeds the buffer limit. |
3 | 11 | The label for one or more effects exceeds the buffer limit. |
4 | 1 | LDCOEF or LDCOV is less than NCOEF. |
3. The cells of the vector FIT are sequenced so that the first variable cycles from 1 to NCLVAL(1) the slowest, the second variable cycles from 1 to NCLVAL(2) the next slowest, etc., up to the NCLVAR‑th variable, which cycles from 1 to NCLVAL(NCLVAR) the fastest.
Example: For NCLVAR = 3, NCLVAL(1) = 2, NCLVAL(2) = 3, and NCLVAL(3) = 2, the cells of table X(I, J, K) are entered into FIT(1) through FIT(12) in the following order: X(1, 1, 1), X(1, 1, 2), X(1, 2, 1), X(1, 2, 2), X(1, 3, 1), X(1, 3, 2), X(2, 1, 1), X(2, 1, 2), X(2, 2, 1), X(2, 2, 2), X(2, 3, 1), X(2, 3, 2).
Example: For NCLVAR = 3, NCLVAL(1) = 2, NCLVAL(2) = 3, and NCLVAL(3) = 2, the cells of table X(I, J, K) are entered into FIT(1) through FIT(12) in the following order: X(1, 1, 1), X(1, 1, 2), X(1, 2, 1), X(1, 2, 2), X(1, 3, 1), X(1, 3, 2), X(2, 1, 1), X(2, 1, 2), X(2, 2, 1), X(2, 2, 2), X(2, 3, 1), X(2, 3, 2).
4. INDEF is used to describe the marginal tables to be fit. For example, if NCLVAR = 3 and the first effect is to fit the marginal table for variables 1 and 3 and the second effect is to fit the marginal table for variable 2, then: NEF = 2, NVEF(1) = 2, and NVEF(2) = 1. Since the sum of the NVEF(I) is 3, then INDEF is a vector of length 3 with values: INDEF(1) = 1, INDEF(2) = 3, and INDEF(3) = 2.
Example
The example illustrates the use of CTPAR in a simple four‑way table in which the first three factors have two levels, and the fourth factor has three levels. The data, which is taken from Lee (1977), involve the brand preference in different situations.
USE PRPFT_INT
USE CTPAR_INT
IMPLICIT NONE
INTEGER IPRINT, LDCOEF, LDCOV, LTAB, NCLVAR
PARAMETER (IPRINT=2, LDCOEF=13, LDCOV=13, LTAB=24, NCLVAR=4)
!
INTEGER INDEF(6), NCLVAL(NCLVAR), NCOEF, NVEF(3)
REAL COEF(LDCOEF,4), COV(LDCOV,LDCOV), FIT(LTAB), &
TABLE(LTAB)
!
DATA TABLE/19, 57, 29, 63, 29, 49, 27, 53, 23, 47, 33, 66, 47, &
55, 23, 50, 24, 37, 42, 68, 43, 52, 30, 42/
DATA NVEF/2, 2, 2/, INDEF/2, 4, 1, 4, 2, 3/
DATA NCLVAL/3, 2, 2, 2/, FIT/24*1.0/
!
CALL PRPFT (NCLVAL, TABLE, NVEF, INDEF, FIT)
!
CALL CTPAR (NCLVAL, NVEF, INDEF, FIT, NCOEF, COEF, COV, IPRINT=IPRINT)
!
END
Output
Variable Number of Levels
1 A 3
2 B 2
3 C 2
4 D 2
----------
Table 1: B = 1 C = 1
D (row) by A (column)
1 2 3
1 19.52 23.65 26.09
2 47.85 46.99 42.89
----------
Table 2: B = 1 C = 2
D (row) by A (column)
1 2 3
1 28.39 34.40 37.94
2 69.58 68.32 62.37
----------
Table 3: B = 2 C = 1
D (row) by A (column)
1 2 3
1 30.85 37.37 41.23
2 57.52 56.48 51.56
----------
Table 4: B = 2 C = 2
D (row) by A (column)
1 2 3
1 25.24 30.58 33.73
2 47.06 46.21 42.18
Coefficient Statistics
Standard Asymptotic
Coefficient Error Z-statistic P-value
1 intercept 3.6827 0.0333 110.66 0.0000
2 A(1) -0.0591 0.0475 -1.24 0.2341
3 A(2) 0.0278 0.0461 0.60 0.5562
4 B -0.0166 0.0331 -0.50 0.6242
5 C -0.0434 0.0319 -1.36 0.1943
6 D -0.2783 0.0329 -8.45 0.0000
7 A*D(1) -0.1016 0.0475 -2.14 0.0506
8 A*D(2) 0.0034 0.0461 0.07 0.9414
9 B*C -0.1438 0.0319 -4.51 0.0005
10 B*D -0.0684 0.0328 -2.09 0.0558
Asymptotic Coefficient Covariance
1 2 3 4 5
1 1.1076E-03 9.7132E-05 -3.5887E-05 4.3244E-05 4.3786E-05
2 2.2562E-03 -1.1408E-03 -3.4043E-11 2.6829E-11
3 2.1232E-03 2.5675E-11 -5.1643E-11
4 1.0968E-03 1.4480E-04
5 1.0146E-03
6 7 8 9 10
1 2.9815E-04 1.3065E-04 -1.6147E-05 1.4480E-04 7.6307E-05
2 1.3065E-04 7.2117E-04 -4.0976E-04 6.2343E-11 -1.0681E-11
3 -1.6147E-05 -4.0976E-04 5.7437E-04 -4.9217E-11 -2.3482E-11
4 7.6307E-05 1.2601E-11 -4.1730E-11 4.3786E-05 2.8917E-04
5 -1.4272E-11 -5.5301E-11 4.2801E-11 4.5231E-06 -4.6962E-11
6 1.0851E-03 9.7132E-05 -3.5887E-05 -4.9749E-11 3.0847E-05
7 2.2562E-03 -1.1408E-03 5.9300E-11 -1.0361E-10
8 2.1232E-03 -2.4481E-11 2.9160E-11
9 1.0146E-03 1.1201E-11
10 1.0743E-03
Published date: 03/19/2020
Last modified date: 03/19/2020
