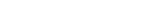FRVAR
Computes the factor structure and the variance explained by each factor.
Required Arguments
A — NVAR by NF matrix of unrotated factor loadings. (Input)
T — NF by NF factor rotation matrix. (Input)
VAR — Vector of length NVAR containing the variances of the original variables. (Input)
If standardized variables were used (i.e., the loadings are from a correlation matrix), then set VAR(1) to any negative number. In this case, VAR may be dimensioned of length one.
If standardized variables were used (i.e., the loadings are from a correlation matrix), then set VAR(1) to any negative number. In this case, VAR may be dimensioned of length one.
S — NVAR by NF factor structure matrix. (Output)
FVAR — Vector of length NF containing the variance accounted for by each of the NF rotated factors. (Output)
Optional Arguments
NVAR — Number of variables. (Input)
Default: NVAR = size (A,1).
Default: NVAR = size (A,1).
NF — Number of factors. (Input)
Default: NF = size (A,2).
Default: NF = size (A,2).
LDA — Leading dimension of A exactly as specified in the dimension statement in the calling program. (Input)
Default: LDA = size (A,1).
Default: LDA = size (A,1).
LDT — Leading dimension of T exactly as specified in the dimension statement in the calling program. (Input)
Default: LDT = size (T,1).
Default: LDT = size (T,1).
LDS — Leading dimension of S exactly as specified in the dimension statement in the calling program. (Input)
Default: LDS = size (S,1).
Default: LDS = size (S,1).
FORTRAN 90 Interface
Generic: CALL FRVAR (A, T, VAR, S, FVAR [, …])
Specific: The specific interface names are S_FRVAR and D_FRVAR.
FORTRAN 77 Interface
Single: CALL FRVAR (NVAR, NF, A, LDA, T, LDT, VAR, S, LDS, FVAR)
Double: The double precision name is DFRVAR.
Description
Routine FRVAR computes the factor structure matrix (the matrix of correlations between the observed variables and the hypothesized factors) and the variance explained by each of the factors (for orthogonal rotations). For oblique rotations, FRVAR computes a measure of the importance of the factors, the sum of the squared elements in each column.
Let Δ denote the diagonal matrix containing the elements of the vector VAR along its diagonal. The estimated factor structure matrix S is computed as
while the elements of FVAR are computed as the diagonal elements of
If the factors were obtained from a correlation matrix (or the factor variances for standardized variables are desired), then the elements of the vector VAR should either all be 1.0, or the first element of VAR should be set to any negative number. In either case, variances of 1.0 are used.
The user should be careful to input the unrotated loadings. When obliquely rotated loadings are input, the output vector FVAR contains a measure of each factors importance, but it does not contain the variance of each factor.
Comments
Workspace may be explicitly provided, if desired, by use of F2VAR/DF2VAR. The reference is
CALL F2VAR (NVAR, NF, A, LDA, T, LDT, VAR, S, LDS, FVAR, TINV, WK, IWK)
The additional arguments are as follows:
TINV — Work vector of length NF2.
WK — Work vector of NF * (1 + NVAR).
IWK — Work vector of length NF.
Example
The following example illustrates the use of routine FRVAR when the structure and an index of factor importance for obliquely rotated loadings (obtained from routine FDOBL) are desired. Note in this example that the elements of FVAR are not variances since the rotation is oblique.
USE FRVAR_INT
USE WRRRN_INT
IMPLICIT NONE
INTEGER LDA, LDS, LDT, NF, NVAR
PARAMETER (LDA=9, LDS=9, LDT=3, NF=3, NVAR=9)
!
REAL A(LDA,NF), FVAR(NF), S(LDS,NF), T(LDT,NF), VAR(NVAR)
!
DATA A/.6642, .6888, .4926, .8372, .7050, .8187, .6615, .4579, &
.7657, -.3209, -.2471, -.3022, .2924, .3148, .3767, -.3960, &
-.2955, -.4274, .0735, -.1933, -.2224, -.0354, -.1528, .1045, &
-.0778, .4914, -.0117/
!
DATA T/0.611, 0.923, 0.042, -0.462, 0.813, 0.728, 0.203, -0.249, &
1.050/
!
DATA VAR/9*1.0/
!
CALL FRVAR (A, T, VAR, S, FVAR)
!
CALL WRRRN ('S', S)
CALL WRRRN ('FVAR', FVAR, 1, NF, 1)
END
Output
S
1 2 3
1 0.3958 -0.6825 0.5274
2 0.4662 -0.7385 0.3093
3 0.2715 -0.6171 0.2052
4 0.8673 -0.5328 0.3010
5 0.7712 -0.4473 0.1338
6 0.8897 -0.4348 0.3654
7 0.3606 -0.7618 0.4397
8 0.2160 -0.3860 0.7270
9 0.4303 -0.8437 0.5566
FVAR
1 2 3
2.170 2.559 0.915
Published date: 03/19/2020
Last modified date: 03/19/2020