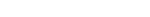LFIHF
Uses iterative refinement to improve the solution of a complex Hermitian system of linear equations.
Required Arguments
A — Complex N by N matrix containing the coefficient matrix of the Hermitian linear system. (Input)
Only the upper triangle of A is referenced.
Only the upper triangle of A is referenced.
FACT — Complex N by N matrix containing the factorization of the coefficient matrix A as output from routine LFCHF/DLFCHF or LFTHF/DLFTHF. (Input)
Only the upper triangle of FACT is used.
Only the upper triangle of FACT is used.
IPVT — Vector of length N containing the pivoting information for the factorization of A as output from routine LFCHF/DLFCHF or LFTHF/DLFTHF. (Input)
B — Complex vector of length N containing the right-hand side of the linear system. (Input)
X — Complex vector of length N containing the solution. (Output)
RES — Complex vector of length N containing the residual vector at the improved solution. (Output)
Optional Arguments
N — Number of equations. (Input)
Default: N = size (A,2).
Default: N = size (A,2).
LDA — Leading dimension of A exactly as specified in the dimension statement of the calling program. (Input)
Default: LDA = size (A,1).
Default: LDA = size (A,1).
LDFACT — Leading dimension of FACT exactly as specified in the dimension statement of the calling program. (Input)
Default: LDFACT = size (FACT,1).
Default: LDFACT = size (FACT,1).
FORTRAN 90 Interface
Generic: CALL LFIHF (A, FACT, IPVT, B, X, RES [, …])
Specific: The specific interface names are S_LFIHF and D_LFIHF.
FORTRAN 77 Interface
Single: CALL LFIHF (N, A, LDA, FACT, LDFACT, IPVT, B, X, RES)
Double: The double precision name is DLFIHF.
Description
Routine LFIHF computes the solution of a system of linear algebraic equations having a complex Hermitian indefinite coefficient matrix.
Iterative refinement is performed on the solution vector to improve the accuracy. Usually almost all of the digits in the solution are accurate, even if the matrix is somewhat ill-conditioned.
To compute the solution, the coefficient matrix must first undergo a U DUH factorization. This may be done by calling either LFCHF or LFTHF.
Iterative refinement fails only if the matrix is very ill-conditioned.
LFIHF and LFSHF both solve a linear system given its U DUH factorization. LFIHF generally takes more time and produces a more accurate answer than LFSHF. Each iteration of the iterative refinement algorithm used by LFIHF calls LFSHF.
Comments
Informational error
Type | Code | Description |
|---|---|---|
3 | 3 | The input matrix is too ill-conditioned for iterative refinement to be effective. |
Example
A set of linear systems is solved successively. The right-hand-side vector is perturbed after solving the system each of the first two times by adding 0.2 + 0.2i to the second element.
USE LFIHF_INT
USE UMACH_INT
USE LFCHF_INT
USE WRCRN_INT
! Declare variables
INTEGER LDA, N
PARAMETER (LDA=3, N=3)
INTEGER IPVT(N), NOUT
REAL RCOND
COMPLEX A(LDA,LDA), B(N), X(N), FACT(LDA,LDA), RES(N)
!
!
! Set values for A and B
!
! A = ( 3.0+0.0i 1.0-1.0i 4.0+0.0i )
! ( 1.0+1.0i 2.0+0.0i -5.0+1.0i )
! ( 4.0+0.0i -5.0-1.0i -2.0+0.0i )
!
! B = ( 7.0+32.0i -39.0-21.0i 51.0+9.0i )
!
DATA A/(3.0,0.0), (1.0,1.0), (4.0,0.0), (1.0,-1.0), (2.0,0.0),&
(-5.0,-1.0), (4.0,0.0), (-5.0,1.0), (-2.0,0.0)/
DATA B/(7.0,32.0), (-39.0,-21.0), (51.0,9.0)/
! Set output unit number
CALL UMACH (2, NOUT)
! Factor A and compute the estimate
! of the reciprocal condition number
CALL LFCHF (A, FACT, IPVT, RCOND)
WRITE (NOUT,99998) RCOND, 1.0E0/RCOND
! Solve, then perturb right-hand side
DO 10 I=1, 3
CALL LFIHF (A, FACT, IPVT, B, X, RES)
! Print results
WRITE (NOUT,99999) I
CALL WRCRN (’X’, X, 1, N, 1)
CALL WRCRN (’RES’, RES, 1, N, 1)
B(2) = B(2) + (0.2E0, 0.2E0)
10 CONTINUE
!
99998 FORMAT (’ RCOND = ’,F5.3,/,’ L1 Condition number = ’,F6.3)
99999 FORMAT (//,’ For problem ’, I1)
END
Output
RCOND < 0.25
L1 Condition number < 5.0
For problem 1
X
1 2 3
( 2.00, 1.00) (-10.00, -1.00) ( 3.00, 5.00)
RES
1 2 3
( 2.384E-07,-4.768E-07) ( 0.000E+00,-3.576E-07) (-1.421E-14, 1.421E-14)
For problem 2
X
1 2 3
( 2.016, 1.032) (-9.971,-0.971) ( 2.973, 4.976)
RES
1 2 3
( 2.098E-07,-1.764E-07) ( 6.231E-07,-1.518E-07) ( 1.272E-07, 4.005E-07)
For problem 3
X
1 2 3
( 2.032, 1.064) (-9.941,-0.941) ( 2.947, 4.952)
RES
1 2 3
( 4.196E-07,-3.529E-07) ( 2.925E-07,-3.632E-07) ( 2.543E-07, 3.242E-07)