CLINK
Performs a hierarchical cluster analysis given a distance matrix.
Required Arguments
DIST — NPT by NPT matrix containing the distance (or similarity) matrix.(Input/Output)
DIST is a symmetric matrix. On input, only the upper triangular part needs to be present. The routine CLINK saves the upper triangular part of DIST in the lower triangle. On return from CLINK, the upper triangular part of DIST is restored, and the matrix has been made symmetric.
DIST is a symmetric matrix. On input, only the upper triangular part needs to be present. The routine CLINK saves the upper triangular part of DIST in the lower triangle. On return from CLINK, the upper triangular part of DIST is restored, and the matrix has been made symmetric.
CLEVEL — Vector of length NPT ‑ 1 containing the level at which the clusters are joined. (Output)
CLEVEL(k) contains the distance (or similarity) level at which cluster NPT + k was formed. If the original data in DIST was transformed via the option parameter IDIST, the inverse transformation is applied to the values in CLEVEL prior to exit from CLINK.
CLEVEL(k) contains the distance (or similarity) level at which cluster NPT + k was formed. If the original data in DIST was transformed via the option parameter IDIST, the inverse transformation is applied to the values in CLEVEL prior to exit from CLINK.
ICLSON — Vector of length NPT ‑ 1 containing the left sons of each merged cluster. (Output)
Cluster NPT + k is formed by merging clusters ICLSON(k) and ICRSON(k).
Cluster NPT + k is formed by merging clusters ICLSON(k) and ICRSON(k).
ICRSON — Vector of length NPT ‑ 1 containing the right sons of each merged cluster. (Output)
Cluster NPT + k is formed by merging clusters ICLSON(k) and ICRSON(k).
Cluster NPT + k is formed by merging clusters ICLSON(k) and ICRSON(k).
Optional Arguments
NPT — Number of data points to be clustered. (Input)
Default: NPT = size (DIST,2).
Default: NPT = size (DIST,2).
IMETH — Option giving the method to be used for clustering. (Input)
Default: IMETH = 0.
Default: IMETH = 0.
IMETH | Method |
|---|---|
0 | Single linkage (minimum distance) |
1 | Complete linkage (maximum distance) |
2 | Average distance within (average distance between objects within the merged cluster) |
3 | Average distance between (average distance between objects in the two clusters) |
4 | Ward’s method (minimize the within‑cluster sums of squares). For Ward’s method, the elements of DIST are assumed to be Euclidean distances. |
IDIST — Option giving the type of transformation to be applied to the measures in DIST. (Input)
Default: IDIST = 0.
Default: IDIST = 0.
IDIST | Transformation |
|---|---|
0 | No transformation is required. The elements of DIST are distances. |
1 | Convert similarities to distances by multiplication by ‑1.0. |
2 | Convert similarities (usually correlations) to distances by taking the reciprocal of the absolute value. |
LDDIST — Leading dimension of DIST exactly as specified in the dimension statement in the calling program. (Input)
Default: LDDIST = size (DIST,1).
Default: LDDIST = size (DIST,1).
FORTRAN 90 Interface
Generic: CALL CLINK (DIST, CLEVEL, ICLSON, ICRSON [, …])
Specific: The specific interface names are S_CLINK and D_CLINK.
FORTRAN 77 Interface
Single: CALL CLINK (NPT, IMETH, IDIST, DIST, LDDIST, CLEVEL, ICLSON, ICRSON)
Double: The double precision name is DCLINK.
Description
Routine CLINK performs hierarchical cluster analysis based upon a distance matrix, or by appropriate use of the IDIST option, based upon a similarity matrix. Only the upper triangular part of the matrix needs to be input to CLINK.
Hierarchical clustering in CLINK proceeds as follows. Initially, each data point is considered to be a cluster, numbered 1 to n = NPT.
1. If the data matrix contains similarities, they are converted to distances by the method specified in IDIST. Set k = 1.
2. A search is made of the distance matrix to find the two closest clusters. These clusters are merged to form a new cluster, numbered n + k. The cluster numbers of the two clusters joined at this stage are saved in ICRSON and ICLSON, and the distance measure between the two clusters is stored in CLEVEL.
3. Based upon the method of clustering, updating of the distance measure in the row and column of DIST corresponding to the new cluster is performed.
4. Set k = k + 1. If k < n, go to Step 2.
The five methods differ primarily in how the distance matrix is updated after two clusters have been joined. The IMETH option parameter specifies how the distance of the cluster just merged with each of the remaining clusters will be updated. Routine CLINK allows five methods of computing the distances. To understand these measures, suppose in the following discussion that clusters “A” and “B” have just been joined to form cluster “Z”, and interest is in computing the distance of Z with another cluster called “C”.
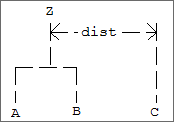
IMETH | Method |
|---|---|
0 | This is the single linkage method. The distance from Z to C is the minimum of the distances (A to C, B to C). |
1 | This is the complete linkage method. The distance from Z to C is the maximum of the distances (A to C, B to C). |
2 | This is the average‑distance‑within‑clusters method. The distance from Z to C is the average distance of all objects that would be within the cluster formed by merging clusters Z and C. This average may be computed according to formulas given by Anderberg (1973, page 139). |
3 | This is the average‑distance‑between‑clusters method. The distance from Z to C is the average distance of objects within cluster Z to objects within cluster C. This average may be computed according to methods given by Anderberg (1973, page 140). |
4 | This is Ward’s method. Clusters are formed so as to minimize the increase in the within‑cluster sums of squares. The distance between two clusters is the increase in these sums of squares if the two clusters were merged. A method for computing this distance from a squared Euclidean distance matrix is given by Anderberg (1973, pages 142‑145). |
In general, single linkage will yield long thin clusters while complete linkage will yield clusters that are more spherical. Average linkage and Ward’s linkage tend to yield clusters that are similar to those obtained with complete linkage.
Routine CLINK produces a unique representation of the binary cluster tree via the following three conventions; the fact that the tree is unique should aid in interpreting the clusters. First, when two clusters are joined and each cluster contains two or more data points, the cluster that was initially formed with the smallest level (in CLEVEL) becomes the left son. Second, when a cluster containing more than one data point is joined with a cluster containing a single data point, the cluster with the single data point becomes the right son. Finally, when two clusters containing only one object are joined, the cluster with the smallest cluster number becomes the right son.
Comments
1. Workspace may be explicitly provided, if desired, by use of C2INK/DC2INK. The reference is:
CALL C2INK (NPT, IMETH, IDIST, DIST, LDDIST, CLEVEL, ICLSON, ICRSON, IPTR, ICLUS, CWT, CSUM)
The additional arguments are as follows:
IPTR — Integer work vector of length NPT.
ICLUS — Integer work vector of length NPT.
CWT — Work vector of length NPT. Not used if IMETH = 0 or 1.
CSUM — Work vector of length NPT. Not used if IMETH = 0 or 1.
2. The clusters corresponding to the original data points are numbered from 1 to NPT. The NPT ‑ 1 clusters formed by merging clusters are numbered NPT + 1 to NPT + (NPT ‑ 1).
3. Raw correlations, if used as similarities, should be made positive and transformed to a distance measure. One such transformation can be performed by specifying IDIST = 2 in CLINK.
4. The user may cluster either variables or observations in CLINK since a dissimilarity matrix, not the original data, is used. Routine CDIST may be used to compute the matrix DIST.
Routine TREEP (see Chapter 16, “Line Printer Graphics”) in the graphics chapter can be used to obtain a line printer plot of the clustering tree. Routine CNUMB can be used to obtain the cluster number assigned to each of the original clusters when a specified number of clusters is desired.
Example
In the following example, the average distance within clusters method is used to perform a hierarchical cluster analysis of the Fisher iris data. Routine GDATA (see Chapter 19, “Utilities”) first used to obtain the Fisher iris data. The example is typical in that after the program obtains the data, routine CDIST computes the distance matrix (DIST) prior to calling CLINK.
USE GDATA_INT
USE CDIST_INT
USE CLINK_INT
USE UMACH_INT
IMPLICIT NONE
INTEGER IDATA, IMETH, IPRINT, IROW, ISCALE, LDDIST, LDX,&
NCOL, NPT, NROW, NVAR
PARAMETER (IDATA=3, IMETH=2, IPRINT=0, IROW=1, ISCALE=1, &
NCOL=5, NROW=150, NVAR=4, LDX=NROW, &
NPT=NROW, LDDIST=LDX)
!
INTEGER I, ICLSON(NROW-1), ICRSON(NROW-1), IND(4), NOUT, &
NXCOL, NXROW
REAL CLEVEL(NROW-1), DIST(LDDIST,LDDIST), X(LDX,NCOL)
!
DATA IND/2, 3, 4, 5/
!
CALL GDATA (IDATA, X, NXROW, NXCOL)
! Compute the distances
CALL CDIST (X, DIST, IND=IND, ISCALE=ISCALE)
! Clustering
CALL CLINK (DIST, CLEVEL, ICLSON, ICRSON, IMETH=IMETH)
! Print some results
CALL UMACH (2, NOUT)
WRITE (NOUT,99996) (I,I=1,149,15)
WRITE (NOUT,99997) (CLEVEL(I),I=1,149,15)
WRITE (NOUT,99998) (ICLSON(I),I=1,149,15)
WRITE (NOUT,99999) (ICRSON(I),I=1,149,15)
!
99996 FORMAT (' OBS # ', 10I6)
99997 FORMAT (' CLEVEL', 10F6.2)
99998 FORMAT (' ICLSON', 10I6)
99999 FORMAT (' ICRSON', 10I6)
!
END
Output
OBS # 1 16 31 46 61 76 91 106 121 136
CLEVEL 0.00 0.17 0.23 0.27 0.31 0.37 0.41 0.48 0.60 0.78
ICLSON 143 153 17 140 53 198 186 218 261 249
ICRSON 102 29 6 113 51 91 212 243 266 262





