TNDF
This function evaluates the noncentral Student’s t cumulative distribution function.
Function Return Value
TNDF — Function value, the probability that a noncentral Student’s t random variable takes a value less than or equal to T. (Output)
Required Arguments
T — Argument for which the noncentral Student’s t cumulative distribution function is to be evaluated. (Input)
IDF — Number of degrees of freedom of the noncentral Student’s t cumulative distribution. (Input)
IDF must be positive.
IDF must be positive.
DELTA — The noncentrality parameter. (Input)
FORTRAN 90 Interface
Generic: TNDF (T, IDF, DELTA)
Specific: The specific interface names are S_TNDF and D_TNDF.
FORTRAN 77 Interface
Single: TNDF (T, IDF, DELTA)
Double: The double precision name is DTNDF.
Description
Function TNDF evaluates the cumulative distribution function F of a noncentral t random variable with IDF degrees of freedom and noncentrality parameter DELTA; that is, with ν = IDF, δ = DELTA, and t0 = T,
where Γ(⋅) is the gamma function. The value of the distribution function at the point t0 is the probability that the random variable takes a value less than or equal to t0.
The noncentral t random variable can be defined by the distribution function above, or alternatively and equivalently, as the ratio of a normal random variable and an independent chi‑squared random variable. If w has a normal distribution with mean δ and variance equal to one, u has an independent chi‑squared distribution with ν degrees of freedom, and
then x has a noncentral t distribution with ν degrees of freedom and noncentrality parameter δ.
The distribution function of the noncentral t can also be expressed as a double integral involving a normal density function (see, for example, Owen 1962, page 108). The function TNDF uses the method of Owen (1962, 1965), which uses repeated integration by parts on that alternate expression for the distribution function.
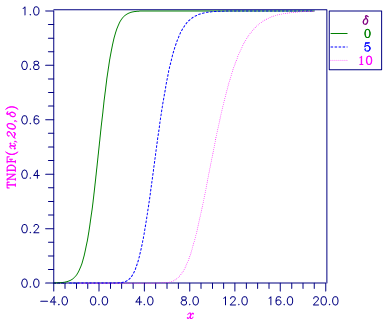
Figure 34, Noncentral Student’s t Distribution Function
Comments
Informational error
Type | Code | Description |
|---|---|---|
4 | 2 | An accurate result cannot be computed due to possible underflow for the machine precision available. DELTA*SQRT(IDF/(IDF+T**2)) must be less than SQRT(-1.9*ALOG(S)), where S=AMACH(1). |
Example
Suppose T is a noncentral t random variable with 6 degrees of freedom and noncentrality parameter 6. In this example, we find the probability that T is less than 12.0. (This can be checked using the table on page 111 of Owen 1962, with η = 0.866, which yields λ = 1.664.)
USE UMACH_INT
USE TNDF_INT
IMPLICIT NONE
INTEGER IDF, NOUT
REAL DELTA, P, T
!
CALL UMACH (2, NOUT)
IDF = 6
DELTA = 6.0
T = 12.0
P = TNDF(T,IDF,DELTA)
WRITE (NOUT,99999) P
99999 FORMAT (' The probability that T is less than 12.0 is ', F6.4)
END
Output
The probability that T is less than 12.0 is 0.9501





