RLMV
Fits a multiple linear regression model using the minimax criterion.
Required Arguments
X — NOBS by NCOL matrix containing the data. (Input)
IIND — Independent variable option. (Input)
The absolute value of IIND is the number of independent (explanatory) variables. The sign of IIND specifies the following options :
The absolute value of IIND is the number of independent (explanatory) variables. The sign of IIND specifies the following options :
IIND | Meaning |
< 0 | The data for the ‑IIND independent variables are given in the first ‑IIND columns of X. |
> 0 | The data for the IIND independent variables are in the columns of X whose column numbers are given by the elements of INDIND. |
= 0 | There are no independent variables. |
The regressors are the constant regressor (if INTCEP = 1) and the independent variables.
INDIND — Index vector of length IIND containing the column numbers of X that are the independent (explanatory) variables. (Input, if IIND is positive)
If IIND is negative, INDIND is not referenced and can be a vector of length one.
If IIND is negative, INDIND is not referenced and can be a vector of length one.
IRSP — Column number IRSP of X contains the data for the response (dependent) variable. (Input)
B — Vector of length INTCEP + ∣IIND∣ containing a minimax solution for the regression coefficients. (Output)
If INTCEP = 1, B(1) contains the intercept estimate. B(INTCEP + I) contains the coefficient estimate for the I-th independent variable.
If INTCEP = 1, B(1) contains the intercept estimate. B(INTCEP + I) contains the coefficient estimate for the I-th independent variable.
Optional Arguments
NOBS — Number of observations. (Input)
Default: NOBS = size (X,1).
Default: NOBS = size (X,1).
NCOL — Number of columns in X. (Input)
Default: NCOL = size (X,2).
Default: NCOL = size (X,2).
LDX — Leading dimension of X exactly as specified in the dimension statement in the calling program. (Input)
Default: LDX = size (X,1).
Default: LDX = size (X,1).
INTCEP — Intercept option. (Input)
Default: INTCEP = 1.
Default: INTCEP = 1.
INTCEP | Action |
0 | An intercept is not in the model. |
1 | An intercept is in the model. |
IRANK — Rank of the matrix of regressors. (Output)
If IRANK is less than INTCEP + ∣IIND∣, linear dependence of the regressors was declared.
If IRANK is less than INTCEP + ∣IIND∣, linear dependence of the regressors was declared.
AEMAX — Magnitude of the largest residual. (Output)
ITER — Number of iterations performed. (Output)
NRMISS — Number of rows of data containing NaN (not a number) for the dependent or independent variables. (Output)
If a row of data contains NaN for any of these variables, that row is excluded from the computations.
If a row of data contains NaN for any of these variables, that row is excluded from the computations.
FORTRAN 90 Interface
Generic: CALL RLMV (X, IIND, INDIND, IRSP, B [, …])
Specific: The specific interface names are S_RLMV and D_RLMV.
FORTRAN 77 Interface
Single: CALL RLMV (NOBS, NCOL, X, LDX, INTCEP, IIND, INDIND, IRSP, B, IRANK, AEMAX, ITER, NRMISS)
Double: The double precision name is DRLMV.
Description
Routine RLMV computes estimates of the regression coefficients in a multiple linear regression model. The criterion satisfied is the minimization of the maximum deviation of the observed response yi from the fitted response for a set on n observations. Under this criterion, known as the minimax or LMV (least maximum value) criterion, the regression coefficient estimates minimize
The estimation problem can be posed as a linear programming problem. A dual simplex algorithm is appropriate, however, the special nature of the problem allows for considerable gains in efficiency by modification of the dual simplex iterations so as to move more rapidly toward the optimal solution. The modifications are described in detail by Barrodale and Phillips (1975).
When multiple solutions exist for a given problem, RLMV may yield different estimates of the regression coefficients on different computers, however, the largest residual in absolute value should have the same absolute value (within rounding differences). The informational error indicating nonunique solutions may result from rounding accumulation. Conversely, because of rounding, the error may fail to result even when the problem does have multiple solutions.
Comments
1. Workspace may be explicitly provided, if desired, by use of R2MV/DR2MV. The reference is:
CALL R2MV (NOBS, NCOL, X, LDX, INTCEP, IIND, INDIND, IRSP, B, IRANK, AEMAX, ITER, NRMISS, WK)
The additional argument is:
WK — Workspace of length NOBS * (∣IIND∣ + 5) + 2 * ∣IIND∣ + 3.
2. Informational errors
Type | Code | Description |
|---|---|---|
3 | 1 | The solution may not be unique. |
4 | 1 | Calculations terminated prematurely due to rounding. |
3. If X is not needed, LDX = NOBS, and IIND < 0, then X and the first NOBS * (‑IIND + 1) elements of WK may occupy the same storage locations. The reference would be:
CALL R2MV (NOBS, NCOL, WK, NOBS, INTCEP, IIND,INDIND, IRSP, B, IRANK, AEMAX, ITER, NRMISS, WK)
Example
A straight line fit to a data set is computed under the LMV criterion.
! SPECIFICATIONS FOR PARAMETERS
USE RLMV_INT
USE UMACH_INT
USE WRRRL_INT
IMPLICIT NONE
INTEGER LDX, NCOEF, NCOL, NOBS, J
PARAMETER (NCOEF=2, NCOL=2, NOBS=7, LDX=NOBS)
!
INTEGER IIND, INDIND(1), IRANK, IRSP, ITER, NOUT, &
NRMISS
REAL B(NCOEF), AEMAX, X(LDX,NCOL)
CHARACTER CLABEL(1)*4, RLABEL(1)*4
!
DATA (X(1,J),J=1,NCOL)/0.0, 0.0/
DATA (X(2,J),J=1,NCOL)/1.0, 2.5/
DATA (X(3,J),J=1,NCOL)/2.0, 2.5/
DATA (X(4,J),J=1,NCOL)/3.0, 4.5/
DATA (X(5,J),J=1,NCOL)/4.0, 4.5/
DATA (X(6,J),J=1,NCOL)/4.0, 6.0/
DATA (X(7,J),J=1,NCOL)/5.0, 5.0/
!
IIND = -1
IRSP = 2
!
CALL RLMV (X, IIND, INDIND, IRSP, B, IRANK=IRANK, AEMAX=AEMAX, &
iter=iter, nrmiss=nrmiss)
!
CALL UMACH (2, NOUT)
RLABEL(1) = 'B ='
CLABEL(1) = 'NONE'
CALL WRRRL (' ', B, RLABEL, CLABEL, 1, NCOEF, 1, FMT='(F6.2)')
WRITE (NOUT,*) 'IRANK = ', IRANK
WRITE (NOUT,*) 'AEMAX = ', AEMAX
WRITE (NOUT,*) 'ITER = ', ITER
WRITE (NOUT,*) 'NRMISS = ', NRMISS
END
Output
B = 1.00 1.00
IRANK = 2
AEMAX = 1.00000
ITER = 3
NRMISS = 0
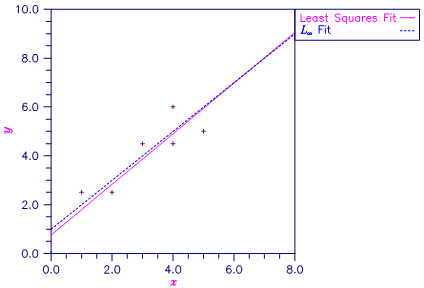
Figure 13, Least Squares and Least Maximum Value Fitted Lines





