BINPR
This function evaluates the binomial probability density function.
Function Return Value
BINPR Function value, the probability that a binomial random variable takes a value equal to K. (Output)
Required Arguments
K — Argument for which the binomial probability function is to be evaluated. (Input)
N — Number of Bernoulli trials. (Input)
PIN — Probability of success on each independent trial. (Input)
FORTRAN 90 Interface
Generic: BINPR (K, N, PIN)
Specific: The specific interface names are S_BINPR and D_BINPR.
FORTRAN 77 Interface
Single: BINPR (K, N, PIN)
Double: The double precision name is DBINPR.
Description
The function BINPR evaluates the probability that a binomial random variable with parameters n and p where p =PIN takes on the value k. It does this by computing probabilities of the random variable taking on the values in its range less than (or the values greater than) k. These probabilities are computed by the recursive relationship
To avoid the possibility of underflow, the probabilities are computed forward from 0, if k is not greater than n times p, and are computed backward from n, otherwise. The smallest positive machine number, ɛ, is used as the starting value for computing the probabilities, which are rescaled by (1 – p)nɛ if forward computation is performed and by pnɛ if backward computation is done.
For the special case of p = 0, BINPR is set to 0 if k is greater than 0 and to 1 otherwise; and for the case p = 1, BINPR is set to 0 if k is less than n and to 1 otherwise.
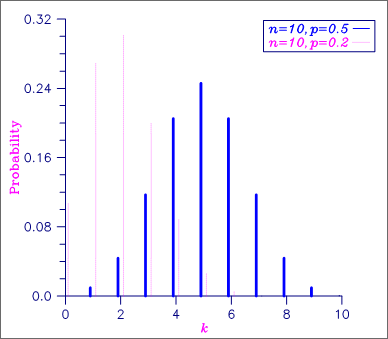
Figure 21, Binomial Probability Function
Comments
Informational errors
Type | Code | Description |
|---|---|---|
1 | 3 | The input argument, K, is less than zero. |
1 | 4 | The input argument, K, is greater than the number of Bernoulli trials, N. |
Example
Suppose X is a binomial random variable with N = 5 and PIN = 0.95. In this example, we find the probability that X is equal to 3.
USE UMACH_INT
USE BINPR_INT
IMPLICIT NONE
INTEGER K, N, NOUT
REAL PIN, PR
!
CALL UMACH (2, NOUT)
K = 3
N = 5
PIN = 0.95
PR = BINPR(K,N,PIN)
WRITE (NOUT,99999) PR
99999 FORMAT (' The probability that X is equal to 3 is ', F6.4)
END
Output
The probability that X is equal to 3 is 0.0214