MATCE
Evaluates a sequence of even, periodic, integer order, real Mathieu functions.
Required Arguments
X — Argument for which the sequence of Mathieu functions is to be evaluated. (Input)
Q — Parameter. (Input)
The parameter Q must be positive.
The parameter Q must be positive.
N — Number of elements in the sequence. (Input)
CE — Vector of length N containing the values of the function through the series. (Output)
CE(I) contains the value of the Mathieu function of order I – 1 at X for I = 1 to N.
CE(I) contains the value of the Mathieu function of order I – 1 at X for I = 1 to N.
FORTRAN 90 Interface
Generic: CALL MATCE (X, Q, N, CE)
Specific: The specific interface names are S_MATCE and D_MATCE.
FORTRAN 77 Interface
Single: CALL MATCE (X, Q, N, CE)
Double: The double precision name is DMATCE.
Description
The eigenvalues of Mathieu’s equation are computed using MATEE. The function values are then computed using a sum of Bessel functions, see Gradshteyn and Ryzhik (1965), equation 8.661.
Comments
1. Workspace may be explicitly provided, if desired, by use of M2TCE/DM2TCE. The reference is
CALL M2TCE (X, Q, N, CE, NORDER, NEEDEV, EVAL0, EVAL1, COEF, WORK, BSJ)
The additional arguments are as follows:
NORDER — Order of the matrix used to compute the eigenvalues. (Input)
It must be greater than N. Routine MATSE computes NORDER by the following call to M3TEE.
It must be greater than N. Routine MATSE computes NORDER by the following call to M3TEE.
CALL M3TEE(Q, N, NORDER)
NEEDEV — Logical variable, if .TRUE., the eigenvalues must be computed. (Input)
EVAL0 — Real work vector of length NORDER containing the eigenvalues computed by MATEE with ISYM = 0 and IPER = 0. (Input/Output)
If NEEDEV is .TRUE., then EVAL0 is computed by M2TCE; otherwise, it must be set as an input value.
If NEEDEV is .TRUE., then EVAL0 is computed by M2TCE; otherwise, it must be set as an input value.
EVAL1 — Real work vector of length NORDER containing the eigenvalues computed by MATEE with ISYM = 0 and IPER = 1. (Input/Output)
If NEEDEV is .TRUE., then EVAL1 is computed by M2TCE; otherwise, it must be set as an input value.
If NEEDEV is .TRUE., then EVAL1 is computed by M2TCE; otherwise, it must be set as an input value.
COEF — Real work vector of length NORDER + 4.
WORK — Real work vector of length NORDER + 4.
BSJ — Real work vector of length 2 * NORDER – 2.
2. Informational error
Type | Code | Description |
|---|---|---|
4 | 1 | The iteration for the eigenvalues did not converge. |
Examples
Example 1
In this example, cen(x = π/4, q = 1), n = 0, …, 9 is computed and printed.
USE CONST_INT
USE MATCE_INT
USE UMACH_INT
IMPLICIT NONE
! Declare variables
INTEGER N
PARAMETER (N=10)
!
INTEGER K, NOUT
REAL CE(N), Q, X
! Compute
Q = 1.0
X = CONST('PI')
X = 0.25* X
CALL MATCE (X, Q, N, CE)
! Print the results
CALL UMACH (2, NOUT)
DO 10 K=1, N
WRITE (NOUT,99999) K-1, X, Q, CE(K)
10 CONTINUE
99999 FORMAT (' ce sub', I2, ' (', F6.3, ',', F6.3, ') = ', F6.3)
END
Output
ce sub 0 ( 0.785, 1.000) = 0.654
ce sub 1 ( 0.785, 1.000) = 0.794
ce sub 2 ( 0.785, 1.000) = 0.299
ce sub 3 ( 0.785, 1.000) = -0.555
ce sub 4 ( 0.785, 1.000) = -0.989
ce sub 5 ( 0.785, 1.000) = -0.776
ce sub 6 ( 0.785, 1.000) = -0.086
ce sub 7 ( 0.785, 1.000) = 0.654
ce sub 8 ( 0.785, 1.000) = 0.998
ce sub 9 ( 0.785, 1.000) = 0.746
Example 2
In this example, we compute cen(x, q) for various values of n and x and a fixed value of q. To avoid having to recompute the eigenvalues, which depend on q but not on x, we compute the eigenvalues once and pass in their value to M2TCE. The eigenvalues are computed using MATEE. The routine M3TEE is used to compute NORDER based on Q and N. The arrays BSJ, COEF and WORK are used as temporary storage in M2TCE.
USE IMSL_LIBRARIES
IMPLICIT NONE
! Declare variables
INTEGER MAXORD, N, NX
PARAMETER (MAXORD=100, N=4, NX=5)
!
INTEGER ISYM, K, NORDER, NOUT
REAL BSJ(2*MAXORD-2), CE(N), COEF(MAXORD+4)
REAL EVAL0(MAXORD), EVAL1(MAXORD), PI, Q, WORK(MAXORD+4), X
! Compute NORDER
Q = 1.0
CALL M3TEE (Q, N, NORDER)
!
CALL UMACH (2, NOUT)
WRITE (NOUT, 99997) NORDER
! Compute eigenvalues
ISYM = 0
CALL MATEE (Q, ISYM, 0, EVAL0)
CALL MATEE (Q, ISYM, 1, EVAL1)
!
PI = CONST('PI')
! Compute function values
WRITE (NOUT, 99998)
DO 10 K=0, NX
X = (K*PI)/NX
CALL M2TCE(X, Q, N, CE, NORDER, .FALSE., EVAL0, EVAL1, &
COEF, WORK, BSJ)
WRITE (NOUT,99999) X, CE(1), CE(2), CE(3), CE(4)
10 CONTINUE
!
99997 FORMAT (' NORDER = ', I3)
99998 FORMAT (/, 28X, 'Order', /, 20X, '0', 7X, '1', 7X, &
'2', 7X, '3')
99999 FORMAT (' ce(', F6.3, ') = ', 4F8.3)
END
Output
NORDER = 23
Order
0 1 2 3
ce( 0.000) = 0.385 0.857 1.086 1.067
ce( 0.628) = 0.564 0.838 0.574 -0.131
ce( 1.257) = 0.926 0.425 -0.575 -0.820
ce( 1.885) = 0.926 -0.425 -0.575 0.820
ce( 2.513) = 0.564 -0.838 0.574 0.131
ce( 3.142) = 0.385 -0.857 1.086 -1.067
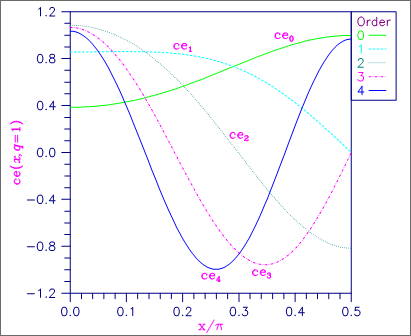
Figure 31, Plot of cen (x, q = 1)