Solves a nonlinear least squares problem subject to bounds on the variables using a modified Levenberg-Marquardt algorithm and a finite-difference Jacobian.
Required Arguments
FCN User-supplied subroutine to evaluate the function to be minimized. The usage is CALL FCN (M, N, X, F), where
M Length of F. (Input)
N Length of X. (Input)
X The point at which
the function is evaluated. (Input)
X should not be
changed by FCN.
F The computed function at the point X. (Output)
FCN must be declared EXTERNAL in the calling program.
M Number of functions. (Input)
IBTYPE Scalar indicating the types of bounds on variables. (Input)
IBTYPE Action
0 User will supply all the bounds.
1 All variables are nonnegative.
2 All variables are nonpositive.
3 User supplies only the bounds on 1st variable, all other variables will have the same bounds.
XLB Vector of length N containing the lower bounds on variables. (Input, if IBTYPE = 0; output, if IBTYPE = 1 or 2; input/output, if IBTYPE = 3)
XUB Vector of length N containing the upper bounds on variables. (Input, if IBTYPE = 0; output, if IBTYPE = 1 or 2; input/output, if IBTYPE = 3)
X Vector of length N containing the approximate solution. (Output)
Optional Arguments
N Number of
variables. (Input)
N must be less than or
equal to M.
Default: N = size
(X,1).
XGUESS Vector
of length N
containing the initial guess. (Input)
Default: XGUESS = 0.0.
XSCALE Vector
of length N
containing the diagonal scaling matrix for the variables. (Input)
XSCALE is
used mainly in scaling the gradient and the distance between two points. By
default, the values for XSCALE are set
internally. See IPARAM(6) in
Comment 4.
FSCALE Vector
of length M
containing the diagonal scaling matrix for the functions. (Input)
FSCALE is
used mainly in scaling the gradient. In the absence of other information, set
all entries to 1.0.
Default: FSCALE = 1.0.
IPARAM
Parameter vector of length 6. (Input/Output)
Set IPARAM(1) to zero for
default values of IPARAM and RPARAM. See
Comment 4.
Default: IPARAM= 0.
RPARAM
Parameter vector of length 7. (Input/Output)
See
Comment 4.
FVEC Vector of length M containing the residuals at the approximate solution. (Output)
FJAC M by N matrix containing a finite difference approximate Jacobian at the approximate solution. (Output)
LDFJAC Leading
dimension of FJAC exactly as
specified in the dimension statement of the calling program.
(Input)
Default: LDFJAC = size
(FJAC ,1).
FORTRAN 90 Interface
Generic: CALL BCLSF (FCN, M, IBTYPE, XLB, XUB, X [, ])
Specific: The specific interface names are S_BCLSF and D_BCLSF.
FORTRAN 77 Interface
Single: CALL BCLSF (FCN, M, N, XGUESS, IBTYPE, XLB, XUB, XSCALE, FSCALE, IPARAM, RPARAM, X, FVEC, FJAC, LDFJAC)
Double: The double precision name is DBCLSF.
Description
The routine BCLSF uses a modified Levenberg-Marquardt method and an active set strategy to solve nonlinear least squares problems subject to simple bounds on the variables. The problem is stated as follows:

subject to l ≤ x ≤ u
where m ≥ n, F : Rn→ Rm, and fi(x) is the i-th component function of F(x). From a given starting point, an active set IA, which contains the indices of the variables at their bounds, is built. A variable is called a free variable if it is not in the active set. The routine then computes the search direction for the free variables according to the formula
d = - (JT J + μI) -1 JT F
where μ is the Levenberg-Marquardt parameter, F = F (x), and J is the Jacobian with respect to the free variables. The search direction for the variables in IA is set to zero. The trust region approach discussed by Dennis and Schnabel (1983) is used to find the new point. Finally, the optimality conditions are checked. The conditions are
||g(xi)|| ≤ ɛ, li < xi< ui
g(xi) < 0, xi = ui
g(xi) > 0, xi = li
where ɛ is a gradient tolerance. This process is repeated until the optimality criterion is achieved.
The active set is changed only when a free variable hits its bounds during an iteration or the optimality condition is met for the free variables but not for all variables in IA, the active set. In the latter case, a variable that violates the optimality condition will be dropped out of IA. For more detail on the Levenberg-Marquardt method, see Levenberg (1944), or Marquardt (1963). For more detailed information on active set strategy, see Gill and Murray (1976).
Since a finite-difference method is used to estimate the Jacobian for some single precision calculations, an inaccurate estimate of the Jacobian may cause the algorithm to terminate at a noncritical point. In such cases, high precision arithmetic is recommended. Also, whenever the exact Jacobian can be easily provided, routine BCLSJ should be used instead.
Comments
1. Workspace may be explicitly provided, if desired, by use of B2LSF/DB2LSF. The reference is:
CALL B2LSF (FCN, M, N, XGUESS, IBTYPE, XLB, XUB, XSCALE, FSCALE, IPARAM, RPARAM, X, FVEC, FJAC, LDFJAC, WK, IWK)
The additional arguments are as follows:
WK Work vector of length 11 * N + 3 * M - 1. WK contains the following information on output: The second N locations contain the last step taken. The third N locations contain the last Gauss-Newton step. The fourth N locations contain an estimate of the gradient at the solution.
IWK Work vector of length 2 * N containing the permutations used in the QR factorization of the Jacobian at the solution.
2. Informational errors
Type Code
3 1 Both the actual and predicted relative reductions in the function are less than or equal to the relative function convergence tolerance.
3 2 The iterates appear to be converging to a noncritical point.
4 3 Maximum number of iterations exceeded.
4 4 Maximum number of function evaluations exceeded.
3 6 Five consecutive steps have been taken with the maximum step length.
2 7 Scaled step tolerance satisfied; the current point may be an approximate local solution, or the algorithm is making very slow progress and is not near a solution, or STEPTL is too big.
3. The first stopping criterion for BCLSF occurs when the norm of the function is less than the absolute function tolerance. The second stopping criterion occurs when the norm of the scaled gradient is less than the given gradient tolerance. The third stopping criterion for BCLSF occurs when the scaled distance between the last two steps is less than the step tolerance.
4. If the default parameters are desired for BCLSF, then set IPARAM(1) to zero and call the routine BCLSF. Otherwise, if any nondefault parameters are desired for IPARAM or RPARAM, then the following steps should be taken before calling BCLSF:
CALL U4LSF (IPARAM, RPARAM)
Set nondefault values for
desired IPARAM, RPARAM elements.
Note that the call to U4LSF will set IPARAM and RPARAM to their default values so only nondefault values need to be set above.
The following is a list of the parameters and the default values:
IPARAM Integer vector of length 6.
IPARAM(1) = Initialization flag.
IPARAM(2) = Number of good digits in the function.
Default: Machine dependent.
IPARAM(3) = Maximum number of iterations.
Default: 100.
IPARAM(4) = Maximum number of function evaluations.
Default: 400.
IPARAM(5) = Maximum number of Jacobian evaluations.
Default: 100.
IPARAM(6) = Internal variable scaling
flag.
If IPARAM(6) = 1, then the values for XSCALE are set
internally.
Default: 1.
RPARAM Real vector of length
7.
RPARAM(1) = Scaled gradient
tolerance.
The i-th component of the scaled gradient at x is
calculated as
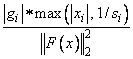
where
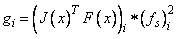
J(x) is the Jacobian, s = XSCALE, and fs = FSCALE.
Default:
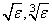
in double where ɛ is the machine precision.
RPARAM(2) = Scaled step tolerance. (STEPTL)
The
i-th component of the scaled step between two points x and y is
computed as
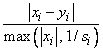
where s = XSCALE.
Default: ɛ2/3 where ɛ is the machine precision.
RPARAM(3) = Relative function tolerance.
Default: max(10 ɛ2/3· max(10-20 , ɛ2/3) in double where ɛ is the machine precision.
RPARAM(4) = Absolute function tolerance.
Default: max (10-20 ɛ2), max(10-40, ɛ2) in double where ɛ is the machine precision.
RPARAM(5) = False convergence tolerance.
Default: 100 ɛ where ɛ is the machine precision.
RPARAM(6) = Maximum allowable step size.
Default: 1000 max(ɛ1, ɛ2) where
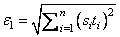
ɛ2 = ||s||2, s = XSCALE, and t = XGUESS.
RPARAM(7) = Size of initial trust region radius.
Default: based on the initial scaled Cauchy step.
If double precision is desired, then DU4LSF is called and RPARAM is declared double precision.
5. Users wishing to override the default print/stop attributes associated with error messages issued by this routine are referred to Error Handling in the Introduction.
Example
The nonlinear least squares problem
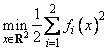
subject to -2 ≤ x1 ≤ 0.5
-1 ≤ x2 ≤ 2
where
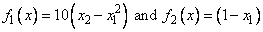
is solved with an initial guess (-1.2, 1.0) and default values for parameters.
USE BCLSF_INT
USE UMACH_INT
IMPLICIT NONE
! Declaration of variables
INTEGER M, N
PARAMETER (M=2, N=2)
!
INTEGER IPARAM(7), ITP, NOUT
REAL FSCALE(M), FVEC(M), X(N), XGUESS(N), XLB(N), XS(N), XUB(N)
EXTERNAL ROSBCK
! Compute the least squares for the
! Rosenbrock function.
DATA XGUESS/-1.2E0, 1.0E0/
DATA XLB/-2.0E0, -1.0E0/, XUB/0.5E0, 2.0E0/
! All the bounds are provided
ITP = 0
! Default parameters are used
IPARAM(1) = 0
!
CALL BCLSF (ROSBCK, M, ITP, XLB, XUB, X, xguess=xguess, &
iparam=iparam, fvec=fvec)
! Print results
CALL UMACH (2, NOUT)
WRITE (NOUT,99999) X, FVEC, IPARAM(3), IPARAM(4)
!
99999 FORMAT (' The solution is ', 2F9.4, //, ' The function ', &
'evaluated at the solution is ', /, 18X, 2F9.4, //, &
' The number of iterations is ', 10X, I3, /, ' The ', &
'number of function evaluations is ', I3, /)
END
!
SUBROUTINE ROSBCK (M, N, X, F)
INTEGER M, N
REAL X(N), F(M)
!
F(1) = 1.0E1*(X(2)-X(1)*X(1))
F(2) = 1.0E0 - X(1)
RETURN
END
Output
The solution is 0.5000
0.2500
The function evaluated at the solution
is
0.0000 0.5000
The number of iterations
is 15
The
number of function evaluations is 20
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |