Minimizes a function of N variables subject to bounds on the variables using a direct search complex algorithm.
Required Arguments
FCN — User-supplied subroutine to evaluate the function to be minimized. The usage is CALL FCN (N, X, F), where
N – Length of X. (Input)
X – Vector of length
N at which point
the function is evaluated. (Input)
X should not be
changed by FCN.
F – The computed function value at the point X. (Output)
FCN must be declared EXTERNAL in the calling program.
IBTYPE — Scalar indicating the types of bounds on variables. (Input)
IBTYPE Action
0 User will supply all the bounds.
1 All variables are nonnegative.
2 All variables are nonpositive.
3 User supplies only the bounds on the first, variable. All other variables will have the same bounds.
XLB — Vector of
length N
containing the lower bounds on the variables. (Input, if
IBTYPE = 0; output, if
IBTYPE = 1 or 2;
input/output, if IBTYPE = 3)
XUB — Vector of
length N
containing the upper bounds on the variables. (Input, if
IBTYPE = 0; output, if
IBTYPE = 1 or 2;
input/output, if IBTYPE = 3)
X — Real vector of length N containing the best estimate of the minimum found. (Output)
Optional Arguments
N — The number of
variables. (Input)
Default: N = size
(XGUESS,1).
XGUESS — Real
vector of length N that contains an
initial guess to the minimum. (Input)
Default: XGUESS = 0.0.
FTOL — First
convergence criterion. (Input)
The algorithm stops when a
relative error in the function values is less than FTOL, i.e. when (F(worst) - F(best)) < FTOL * (1 + ABS(F(best))) where F(worst) and F(best) are the
function values of the current worst and best point, respectively. Second
convergence criterion. The algorithm stops when the standard deviation of the
function values at the 2 * N current points is
less than FTOL.
If the subroutine terminates prematurely, try again with a smaller value FTOL.
Default:
FTOL = 1.0e-4
for single and 1.0d-8 for double precision.
MAXFCN — On
input, maximum allowed number of function evaluations. (Input/
Output)
On output, actual number of function evaluations needed.
Default:
MAXFCN =
300.
FVALUE — Function value at the computed solution. (Output)
FORTRAN 90 Interface
Generic: CALL BCPOL (FCN, IBTYPE, XLB, XUB, X [,…])
Specific: The specific interface names are S_BCPOL and D_BCPOL.
FORTRAN 77 Interface
Single: CALL BCPOL (FCN, N, XGUESS, IBTYPE, XLB, XUB, FTOL, MAXFCN, X, FVALUE)
Double: The double precision name is DBCPOL.
Description
The routine BCPOL uses the complex method to find a minimum point of a function of n variables. The method is based on function comparison; no smoothness is assumed. It starts with 2n points x1, x2, …, x2n. At each iteration, a new point is generated to replace the worst point xj, which has the largest function value among these 2n points. The new point is constructed by the following formula:
xk = c + α(c - xj)
where

and α (α > 0) is the reflection coefficient.
When xk is a best point, that is, when f (xk) ≤ f (xi) for i = 1, …, 2n, an expansion point is computed xe = c + β(xk - c), where β(β > 1) is called the expansion coefficient. If the new point is a worst point, then the complex would be contracted to get a better new point. If the contraction step is unsuccessful, the complex is shrunk by moving the vertices halfway toward the current best point. Whenever the new point generated is beyond the bound, it will be set to the bound. This procedure is repeated until one of the following stopping criteria is satisfied:
Criterion 1:
fbest - fworst ≤ ɛf(1. + |fbest|)
Criterion 2:
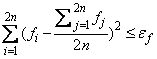
where fi = f(xi), fj = f(xj), and ɛf is a given tolerance. For a complete description, see Nelder and Mead (1965) or Gill et al. (1981).
Comments
1. Workspace may be explicitly provided, if desired, by use of B2POL/DB2POL. The reference is:
CALL B2POL (FCN, N, XGUESS, IBTYPE, XLB, XUB, FTOL, MAXFCN, X, FVALUE, WK)
The additional argument is:
WK — Real work vector of length 2 * N**2 + 5 * N
2. Informational error
Type Code
3 1 The maximum number of function evaluations is exceeded.
3. Since BCPOL uses only function-value information at each step to determine a new approximate minimum, it could be quite inefficient on smooth problems compared to other methods such as those implemented in routine BCONF, which takes into account derivative information at each iteration. Hence, routine BCPOL should only be used as a last resort. Briefly, a set of 2 * N points in an N-dimensional space is called a complex. The minimization process iterates by replacing the point with the largest function value by a new point with a smaller function value. The iteration continues until all the points cluster sufficiently close to a minimum.
Example
The problem
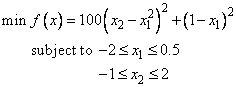
is solved with an initial guess (-1.2, 1.0), and the solution is printed.
USE BCPOL_INT
USE UMACH_INT
IMPLICIT NONE
! Variable declarations
INTEGER N
PARAMETER (N=2)
!
INTEGER IBTYPE, K, NOUT
REAL FTOL, FVALUE, X(N), XGUESS(N), XLB(N), XUB(N)
EXTERNAL FCN
!
! Initializations
! XGUESS = (-1.2, 1.0)
! XLB = (-2.0, -1.0)
! XUB = ( 0.5, 2.0)
DATA XGUESS/-1.2, 1.0/, XLB/-2.0E0, -1.0E0/, XUB/0.5E0, 2.0E0/
!
FTOL = 1.0E-5
IBTYPE = 0
!
CALL BCPOL (FCN, IBTYPE, XLB, XUB, X, xguess=xguess, ftol=ftol, &
fvalue=fvalue)
!
CALL UMACH (2, NOUT)
WRITE (NOUT,99999) (X(K),K=1,N), FVALUE
99999 FORMAT (' The best estimate for the minimum value of the', /, &
' function is X = (', 2(2X,F4.2), ')', /, ' with ', &
'function value FVALUE = ', E12.6)
!
END
! External function to be minimized
SUBROUTINE FCN (N, X, F)
INTEGER N
REAL X(N), F
!
F = 100.0*(X(2)-X(1)*X(1))**2 + (1.0-X(1))**2
RETURN
END
Output
The best estimate for the minimum value of the
function is
X = ( 0.50 0.25)
with function value FVALUE = 0.250002E+00
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |