Computes a three-dimensional tensor-product spline approximant using least squares, returning the tensor-product B-spline coefficients.
Required Arguments
XDATA — Array of
length NXDATA
containing the data points in the x-direction.
(Input)
XDATA must be
nondecreasing.
YDATA — Array of
length NYDATA
containing the data points in the y-direction. (Input)
YDATA must
be nondecreasing.
ZDATA — Array of
length NZDATA
containing the data points in the z-direction. (Input)
ZDATA must
be nondecreasing.
FDATA — Array of
size NXDATA by
NYDATA by NZDATA containing the
values to be interpolated. (Input)
FDATA(I, J, K) contains the value
at (XDATA(I), YDATA(J), ZDATA(K)).
KXORD — Order of the spline in the x-direction. (Input)
KYORD — Order of the spline in the y-direction. (Input)
KZORD — Order of the spline in the z-direction. (Input)
XKNOT — Array of
length KXORD +
NXCOEF
containing the knots in the x-direction. (Input)
XKNOT must be
nondecreasing.
YKNOT — Array of
length KYORD +
NYCOEF
containing the knots in the y-direction. (Input)
YKNOT must be
nondecreasing.
ZKNOT — Array of
length KZORD +
NZCOEF
containing the knots in the z-direction. (Input)
ZKNOT must be
nondecreasing.
BSCOEF — Array of
length NXCOEF*NYCOEF*NZCOEF
that contains the tensor product
B-spline coefficients.
(Output)
Optional Arguments
NXDATA — Number
of data points in the x-direction.
(Input)
NXDATA must be greater
than or equal to NXCOEF.
Default:
NXDATA =
size (XDATA,1).
NYDATA — Number
of data points in the y-direction. (Input)
NYDATA must be greater
than or equal to NYCOEF.
Default:
NYDATA =
size (YDATA,1).
NZDATA — Number
of data points in the z-direction. (Input)
NZDATA must be greater
than or equal to NZCOEF.
Default:
NZDATA =
size (ZDATA,1).
LDFDAT — Leading
dimension of FDATA exactly as
specified in the dimension statement of the calling program.
(Input)
Default: LDFDAT = size (FDATA,1).
MDFDAT — Second
dimension of FDATA exactly as
specified in the dimension statement of the calling program.
(Input)
Default: MDFDAT = size (FDATA,2).
NXCOEF — Number
of B-spline coefficients in the x-direction.
(Input)
Default: NXCOEF = size (XKNOT,1) – KXORD.
NYCOEF — Number
of B-spline coefficients in the y-direction.
(Input)
Default: NYCOEF = size (YKNOT,1) – KYORD.
NZCOEF — Number
of B-spline coefficients in the z-direction.
(Input)
Default: NZCOEF = size (ZKNOT,1) – KZORD.
XWEIGH — Array of
length NXDATA
containing the positive weights of XDATA.
(Input)
Default: XWEIGH = 1.0.
YWEIGH — Array of
length NYDATA
containing the positive weights of YDATA.
(Input)
Default: YWEIGH = 1.0.
ZWEIGH — Array of
length NZDATA
containing the positive weights of ZDATA.
(Input)
Default: ZWEIGH = 1.0.
FORTRAN 90 Interface
Generic: CALL BSLS3 (XDATA, YDATA, ZDATA, FDATA, KXORD, KYORD, KZORD, XKNOT, YKNOT, ZKNOT, BSCOEF [,…])
Specific: The specific interface names are S_BSLS3 and D_BSLS3.
FORTRAN 77 Interface
Single: CALL BSLS3 (NXDATA, XDATA, NYDATA, YDATA, NZDATA, ZDATA, FDATA, LDFDAT, MDFDAT, KXORD, KYORD, KZORD, XKNOT, YKNOT, ZKNOT, NXCOEF, NYCOEF, NZCOEF, XWEIGH, YWEIGH, ZWEIGH, BSCOEF)
Double: The double precision name is DBSLS3.
Description
The routine BSLS3
computes the coefficients of a tensor-product spline least-squares approximation
to weighted tensor-product data. The input for this subroutine consists of data
vectors to specify the tensor-product grid for the data, three vectors with the
weights, the values of the surface on the grid, and the specification for the
tensor-product spline. The grid is specified by the three vectors x =
XDATA,
y = YDATA,
and z = ZDATA
of length k = NXDATA,
l = NYDATA
, and
m = NYDATA,
respectively. A three-dimensional array f = FDATA
contains the data values which are to be fit. The three vectors wx = XWEIGH,
wy = YWEIGH,
and wz = ZWEIGH
contain the weights for the weighted least-squares problem. The information for
the approximating tensor-product spline must also be provided. This information
is contained in kx = KXORD,
tx = XKNOT,
and K = NXCOEF
for the spline in the first variable, in ky = KYORD,
ty = YKNOT
and L = NYCOEF
for the spline in the second variable, and in kz = KZORD,
tz = ZKNOT
and M = NZCOEF
for the spline in the third variable.
The coefficients of the resulting tensor product spline are
returned in c = BSCOEF,
which is an
K × L × M array. The
procedure computes coefficients by solving the normal equations in
tensor-product form as discussed in de Boor (1978, Chapter 17). The interested
reader might also want to study the paper by E. Grosse (1980).
The final result produces coefficients c minimizing
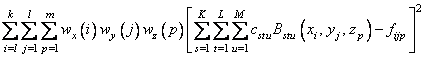
where the function Bstu is the tensor-product of three B-splines of order kx, ky, and kz. Specifically, we have
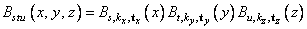
The spline
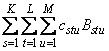
can be evaluated at one point using BS3VL and its partial derivatives can be evaluated using BS3DR. If the values on a grid are desired then we recommend BS3GD.
Comments
1. Workspace may be explicitly provided, if desired, by use of B2LS3/DB2LS3. The reference is:
CALL B2LS3 (NXDATA, XDATA, NYDATA, NZDATA, ZDATA, YDATA, FDATA, LDFDAT, KXORD, KYORD, KZORD, XKNOT, YKNOT, ZKNOT, NXCOEF, NYCOEF, NZCOEF, XWEIGH, YWEIGH, ZWEIGH, BSCOEF, WK)
The additional argument is:
WK — Work
array of length NYCOEF * (NZDATA + KYORD + NZCOEF) + NZDATA *
(1 + NYDATA) + NXCOEF * (KXORD + NYDATA * NZDATA) + KZORD * NZCOEF +
3 *
MAX0(KXORD, KYORD, KZORD).
2. Informational errors
Type Code
3 13 There may be less than one digit of accuracy in the least squares fit. Try using higher precision if possible.
4 7 Multiplicity of knots cannot exceed the order of the spline.
4 8 The knots must be nondecreasing.
4 9 All weights must be greater than zero.
4 10 The data point abscissae must be nondecreasing.
4 11 The smallest element of the data point array must be greater than or equal to the K_ORDth knot.
4 12 The largest element of the data point array must be less than or equal to the (N_COEF + 1)st knot.
Example
The data for this example arise from the function
e(y - z) sin(x +
y) + ɛ on the
rectangle
[0, 3] ×
[0, 2] × [0, 1]. Here,
ɛ is a uniform random
variable with range [−.5, .5]. We sample this
function on a 4 × 3
× 2 grid and then try to
recover it by using tensor-product cubic splines in all variables. We print out
the values of the function e(y - z) sin(x +
y) on a 4 × 3
× 2 grid and compare
these values with the values of the tensor-product spline that was computed
using the IMSL routine BSLS3.
USE BSLS3_INT
USE RNSET_INT
USE RNUNF_INT
USE UMACH_INT
USE BS3GD_INT
IMPLICIT NONE
INTEGER KXORD, KYORD, KZORD, LDFDAT, MDFDAT, NXCOEF, NXDATA,&
NXVAL, NYCOEF, NYDATA, NYVAL, NZCOEF, NZDATA, NZVAL
PARAMETER (KXORD=4, KYORD=4, KZORD=4, NXCOEF=8, NXDATA=15,&
NXVAL=4, NYCOEF=8, NYDATA=15, NYVAL=3, NZCOEF=8,&
NZDATA=15, NZVAL=2, LDFDAT=NXDATA, MDFDAT=NYDATA)
!
INTEGER I, J, K, NOUT
REAL BSCOEF(NXCOEF,NYCOEF,NZCOEF), EXP, F,&
FDATA(NXDATA,NYDATA,NZDATA), FLOAT, RNOISE,&
SIN, SPXYZ(NXVAL,NYVAL,NZVAL), X, XDATA(NXDATA),&
XKNOT(NXCOEF+KXORD), XVAL(NXVAL), XWEIGH(NXDATA), Y,&
YDATA(NYDATA), YKNOT(NYCOEF+KYORD), YVAL(NYVAL),&
YWEIGH(NYDATA), Z, ZDATA(NZDATA),&
ZKNOT(NZCOEF+KZORD), ZVAL(NZVAL), ZWEIGH(NZDATA)
INTRINSIC EXP, FLOAT, SIN
! Define a function
F(X,Y,Z) = EXP(Y-Z)*SIN(X+Y)
!
CALL RNSET (1234579)
CALL UMACH (2, NOUT)
! Set up knot sequences
! X-knots
DO 10 I=1, NXCOEF - KXORD + 2
XKNOT(I+KXORD-1) = 3.0*(FLOAT(I-1)/FLOAT(NXCOEF-KXORD+1))
10 CONTINUE
DO 20 I=1, KXORD - 1
XKNOT(I) = XKNOT(KXORD)
XKNOT(I+NXCOEF+1) = XKNOT(NXCOEF+1)
20 CONTINUE
! Y-knots
DO 30 I=1, NYCOEF - KYORD + 2
YKNOT(I+KYORD-1) = 2.0*(FLOAT(I-1)/FLOAT(NYCOEF-KYORD+1))
30 CONTINUE
DO 40 I=1, KYORD - 1
YKNOT(I) = YKNOT(KYORD)
YKNOT(I+NYCOEF+1) = YKNOT(NYCOEF+1)
40 CONTINUE
! Z-knots
DO 50 I=1, NZCOEF - KZORD + 2
ZKNOT(I+KZORD-1) = 1.0*(FLOAT(I-1)/FLOAT(NZCOEF-KZORD+1))
50 CONTINUE
DO 60 I=1, KZORD - 1
ZKNOT(I) = ZKNOT(KZORD)
ZKNOT(I+NZCOEF+1) = ZKNOT(NZCOEF+1)
60 CONTINUE
! Set up X-grid.
DO 70 I=1, NXDATA
XDATA(I) = 3.0*(FLOAT(I-1)/FLOAT(NXDATA-1))
70 CONTINUE
! Set up Y-grid.
DO 80 I=1, NYDATA
YDATA(I) = 2.0*(FLOAT(I-1)/FLOAT(NYDATA-1))
80 CONTINUE
! Set up Z-grid
DO 90 I=1, NZDATA
ZDATA(I) = 1.0*(FLOAT(I-1)/FLOAT(NZDATA-1))
90 CONTINUE
! Evaluate the function on the grid
! and add noise.
DO 100 I=1, NXDATA
DO 100 J=1, NYDATA
DO 100 K=1, NZDATA
RNOISE = RNUNF()
RNOISE = RNOISE - 0.5
FDATA(I,J,K) = F(XDATA(I),YDATA(J),ZDATA(K)) + RNOISE
100 CONTINUE
! Use default weights equal to 1.0
!
! Compute least-squares
CALL BSLS3 (XDATA, YDATA, ZDATA, FDATA, KXORD, KYORD, KZORD, XKNOT, &
YKNOT, ZKNOT, BSCOEF)
! Set up grid for evaluation.
DO 110 I=1, NXVAL
XVAL(I) = FLOAT(I-1)
110 CONTINUE
DO 120 I=1, NYVAL
YVAL(I) = FLOAT(I-1)
120 CONTINUE
DO 130 I=1, NZVAL
ZVAL(I) = FLOAT(I-1)
130 CONTINUE
! Evaluate on the grid.
CALL BS3GD (0, 0, 0, XVAL, YVAL, ZVAL, KXORD, KYORD, KZORD, XKNOT, &
YKNOT, ZKNOT, BSCOEF, SPXYZ)
! Print results.
WRITE (NOUT,99998)
DO 140 I=1, NXVAL
DO 140 J=1, NYVAL
DO 140 K=1, NZVAL
WRITE (NOUT,99999) XVAL(I), YVAL(J), ZVAL(K),&
F(XVAL(I),YVAL(J),ZVAL(K)),&
SPXYZ(I,J,K), F(XVAL(I),YVAL(J),ZVAL(K)&
) - SPXYZ(I,J,K)
140 CONTINUE
99998 FORMAT (8X, 'X', 9X, 'Y', 9X, 'Z', 6X, 'F(X,Y,Z)', 3X,&
'S(X,Y,Z)', 4X, 'Error')
99999 FORMAT (' ', 3F10.3, 3F11.4)
END
Output
X
Y
Z F(X,Y,Z) S(X,Y,Z)
Error
0.000 0.000
0.000 0.0000
0.1987
-0.1987
0.000 0.000
1.000 0.0000
0.1447 -0.1447
0.000
1.000 0.000
2.2874 2.2854
0.0019
0.000 1.000
1.000 0.8415
1.0557 -0.2142
0.000
2.000 0.000
6.7188 6.4704
0.2484
0.000 2.000
1.000 2.4717
2.2054 0.2664
1.000
0.000 0.000
0.8415 0.8779
-0.0365
1.000 0.000
1.000 0.3096
0.2571 0.0524
1.000
1.000 0.000
2.4717 2.4015
0.0703
1.000 1.000
1.000 0.9093
0.8995 0.0098
1.000
2.000 0.000
1.0427 1.1330
-0.0902
1.000 2.000
1.000 0.3836
0.4951 -0.1115
2.000
0.000 0.000
0.9093 0.8269
0.0824
2.000 0.000
1.000 0.3345
0.3258
0.0087
2.000 1.000
0.000 0.3836
0.3564 0.0272
2.000
1.000 1.000
0.1411 0.1905
-0.0494
2.000 2.000
0.000 -5.5921 -5.5362
-0.0559
2.000 2.000
1.000 -2.0572 -1.9659
-0.0913
3.000 0.000
0.000 0.1411
0.4841 -0.3430
3.000
0.000 1.000
0.0519 -0.4257
0.4776
3.000 1.000
0.000 -2.0572 -1.9710
-0.0862
3.000 1.000
1.000 -0.7568
-0.8479 0.0911
3.000
2.000 0.000 -7.0855
-7.0957 0.0101
3.000
2.000 1.000 -2.6066
-2.1650 -0.4416
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |