Computes the Akima cubic spline interpolant.
Required Arguments
XDATA — Array of
length NDATA
containing the data point abscissas. (Input)
The data point
abscissas must be distinct.
FDATA — Array of length NDATA containing the data point ordinates. (Input)
BREAK — Array of length NDATA containing the breakpoints for the piecewise cubic representation. (Output)
CSCOEF — Matrix of size 4 by NDATA containing the local coefficients of the cubic pieces. (Output)
Optional Arguments
NDATA — Number of
data points. (Input)
Default: NDATA = size (XDATA,1).
FORTRAN 90 Interface
Generic: CALL CSAKM (XDATA, FDATA, BREAK, CSCOEF [,…])
Specific: The specific interface names are S_CSAKM and D_CSAKM.
FORTRAN 77 Interface
Single: CALL CSAKM (NDATA, XDATA, FDATA, BREAK, CSCOEF)
Double: The double precision name is DCSAKM.
Description
The routine CSAKM
computes a C 1
cubic spline interpolant to a set of data points (xi, fi) for
i = 1,
…, NDATA
= N. The breakpoints of the spline are the abscissas. Endpoint conditions
are automatically determined by the program; see Akima (1970) or de Boor
(1978).
If the data points arise from the values of a smooth (say C 4) function f, i.e. fi = f(xi), then the error will behave in a predictable fashion. Let ξ be the breakpoint vector for the above spline interpolant. Then, the maximum absolute error satisfies
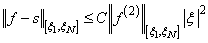
where
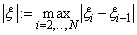
The routine CSAKM is based on a method by Akima (1970) to combat wiggles in the interpolant. The method is nonlinear; and although the interpolant is a piecewise cubic, cubic polynomials are not reproduced. (However, linear polynomials are reproduced.)
Comments
1. Workspace may be explicitly provided, if desired, by use of C2AKMD/C2AKM. The reference is:
CALL C2AKM (NDATA, XDATA, FDATA, BREAK, CSCOEF, IWK)
The additional argument is:
IWK — Work array of length NDATA.
2. The cubic spline can be evaluated using CSVAL; its derivative can be evaluated using CSDER.
3. Note that column NDATA of CSCOEF is used as workspace.
Example
In this example, a cubic spline interpolant to a function f is computed. The values of this spline are then compared with the exact function values.
USE CSAKM_INT
USE UMACH_INT
USE CSVAL_INT
IMPLICIT NONE
INTEGER NDATA
PARAMETER (NDATA=11)
!
INTEGER I, NINTV, NOUT
REAL BREAK(NDATA), CSCOEF(4,NDATA), F,&
FDATA(NDATA), FLOAT, SIN, X, XDATA(NDATA)
INTRINSIC FLOAT, SIN
! Define function
F(X) = SIN(15.0*X)
! Set up a grid
DO 10 I=1, NDATA
XDATA(I) = FLOAT(I-1)/FLOAT(NDATA-1)
FDATA(I) = F(XDATA(I))
10 CONTINUE
! Compute cubic spline interpolant
CALL CSAKM (XDATA, FDATA, BREAK, CSCOEF)
! Get output unit number
CALL UMACH (2, NOUT)
! Write heading
WRITE (NOUT,99999)
99999 FORMAT (13X, 'X', 9X, 'Interpolant', 5X, 'Error')
NINTV = NDATA - 1
! Print the interpolant on a finer grid
DO 20 I=1, 2*NDATA - 1
X = FLOAT(I-1)/FLOAT(2*NDATA-2)
WRITE (NOUT,'(2F15.3,F15.6)') X, CSVAL(X,BREAK,CSCOEF),&
F(X) - CSVAL(X,BREAK,&
CSCOEF)
20 CONTINUE
END
Output
X
Interpolant
Error
0.000
0.000
0.000000
0.050
0.818
-0.135988
0.100
0.997
0.000000
0.150
0.615
0.163487
0.200
0.141
0.000000
0.250
-0.478
-0.093376
0.300
-0.978
0.000000
0.350
-0.812
-0.046447
0.400
-0.279
0.000000
0.450
0.386
0.064491
0.500
0.938
0.000000
0.550
0.854
0.068274
0.600
0.412
0.000000
0.650
-0.276
-0.043288
0.700
-0.880
0.000000
0.750
-0.889
-0.078947
0.800
-0.537
0.000000
0.850
0.149
0.033757
0.900
0.804
0.000000
0.950
0.932
0.061260
1.000
0.650 0.000000
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |