Computes all of the eigenvalues and eigenvectors of a real symmetric matrix in band symmetric storage mode.
Required Arguments
A — Band symmetric matrix of order N. (Input)
NCODA — Number of codiagonals in A. (Input)
EVAL — Vector of length N containing the eigenvalues of A in decreasing order of magnitude. (Output)
EVEC — Matrix of
order N
containing the eigenvectors. (Output)
The J-th eigenvector,
corresponding to EVAL(J), is stored in the
J-th column.
Each vector is normalized to have Euclidean length equal to the value one.
Optional Arguments
N — Order of the
matrix A.
(Input)
Default: N = size
(A,2).
LDA — Leading
dimension of A
exactly as specified in the dimension statement in the calling
program. (Input)
Default: LDA = size
(A,1).
LDEVEC — Leading
dimension of EVEC exactly as
specified in the dimension statement in the calling program.
(Input)
Default: LDEVEC = size
(EVEC,1).
FORTRAN 90 Interface
Generic: CALL EVCSB (A, NCODA, EVAL, EVEC [,…])
Specific: The specific interface names are S_EVCSB and D_EVCSB.
FORTRAN 77 Interface
Single: CALL EVCSB (N, A, LDA, NCODA, EVAL, EVEC, LDEVEC)
Double: The double precision name is DEVCSB.
Description
Routine EVCSB computes the eigenvalues and eigenvectors of a real band symmetric matrix. Orthogonal similarity transformations are used to reduce the matrix to an equivalent symmetric tridiagonal matrix. These transformations are accumulated. The implicit QL algorithm is used to compute the eigenvalues and eigenvectors of the resulting tridiagonal matrix.
The reduction routine is based on the EISPACK routine BANDR; see Garbow et al. (1977). The QL routine is based on the EISPACK routine IMTQL2; see Smith et al. (1976).
Comments
1. Workspace may be explicitly provided, if desired, by use of E4CSB/DE4CSB. The reference is:
CALL E4CSB (N, A, LDA, NCODA, EVAL, EVEC, LDEVEC, COPY, WK, IWK)
The additional arguments are as follows:
ACOPY — Work array of length N(NCODA + 1). A and ACOPY may be the same, in which case the first N * NCODA elements of A will be destroyed.
WK — Work array of length N.
IWK — Integer work array of length N.
2. Informational error
Type Code
4 1 The iteration for the eigenvalues failed to converge.
3. The success of this routine can be checked using EPISB.
Example
In this example, a DATA statement is used to set A to a band matrix given by Gregory and Karney (1969, page 75). The eigenvalues, lk, of this matrix are given by
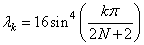
The eigenvalues and eigenvectors of this real band symmetric matrix are computed and printed. The performance index is also computed and printed. This serves as a check on the computations; for more details, see IMSL routine EPISB.
USE EVCSB_INT
USE EPISB_INT
USE UMACH_INT
USE WRRRN_INT
IMPLICIT NONE
! Declare variables
INTEGER LDA, LDEVEC, N, NCODA
PARAMETER (N=6, NCODA=2, LDA=NCODA+1, LDEVEC=N)
!
INTEGER NOUT
REAL A(LDA,N), EVAL(N), EVEC(LDEVEC,N), PI
! Define values of A:
! A = ( 5 -4 1 )
! ( -4 6 -4 1 )
! ( 1 -4 6 -4 1 )
! ( 1 -4 6 -4 1 )
! ( 1 -4 6 -4 )
! ( 1 -4 5 )
! Represented in band symmetric
! form this is:
! A = ( 0 0 1 1 1 1 )
! ( 0 -4 -4 -4 -4 -4 )
! ( 5 6 6 6 6 5 )
!
DATA A/0.0, 0.0, 5.0, 0.0, -4.0, 6.0, 1.0, -4.0, 6.0, 1.0, -4.0, &
6.0, 1.0, -4.0, 6.0, 1.0, -4.0, 5.0/
!
! Find eigenvalues and vectors
CALL EVCSB (A, NCODA, EVAL, EVEC)
! Compute performance index
PI = EPISB(N,A,NCODA,EVAL,EVEC)
! Print results
CALL UMACH (2, NOUT)
CALL WRRRN ('EVAL', EVAL, 1, N, 1)
CALL WRRRN ('EVEC', EVEC)
WRITE (NOUT,'(/,A,F6.3)') ' Performance index = ', PI
END
Output
EVAL
1 2 3 4 5 6
14.45 10.54 5.98 2.42 0.57 0.04
EVEC
1 2 3 4 5 6
1 -0.2319 -0.4179 -0.5211 0.5211 -0.4179 0.2319
2 0.4179 0.5211 0.2319 0.2319 -0.5211 0.4179
3 -0.5211 -0.2319 0.4179 -0.4179 -0.2319 0.5211
4 0.5211 -0.2319 -0.4179 -0.4179 0.2319 0.5211
5 -0.4179 0.5211 -0.2319 0.2319 0.5211 0.4179
6 0.2319 -0.4179 0.5211 0.5211 0.4179 0.2319
Performance index = 0.029
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |