Computes all of the eigenvalues of a real symmetric matrix in band symmetric storage mode.

Required Arguments

A — Band symmetric matrix of order N.   (Input)

NCODA — Number of codiagonals in A.   (Input)

EVAL — Vector of length N containing the eigenvalues of A in decreasing order of magnitude.   (Output)

Optional Arguments

N — Order of the matrix A.   (Input)
Default: N = size (A,2).

LDA — Leading dimension of A exactly as specified in the dimension statement in the calling program.   (Input)
Default: LDA = size (A,1).

FORTRAN 90 Interface

Generic:          CALL EVLSB (A, NCODA, EVAL [,…])

Specific:         The specific interface names are S_EVLSB and D_EVLSB.

FORTRAN 77 Interface

Single:     CALL EVLSB (N, A, LDA, NCODA, EVAL)

Double:          The double precision name is DEVLSB.

Description

Routine EVLSB computes the eigenvalues of a real band symmetric matrix. Orthogonal similarity transformations are used to reduce the matrix to an equivalent symmetric tridiagonal matrix. The implicit QL algorithm is used to compute the eigenvalues of the resulting tridiagonal matrix.

The reduction routine is based on the EISPACK routine BANDR; see Garbow et al. (1977). The QL routine is based on the EISPACK routine IMTQL1; see Smith et al. (1976).

Comments

1.         Workspace may be explicitly provided, if desired, by use of E3LSB/DE3LSB. The reference is:

CALL E3LSB (N, A, LDA, NCODA, EVAL, ACOPY, WK)

The additional arguments are as follows:

ACOPY —  Work array of length N(NCODA + 1). The arrays A and ACOPY may be the same, in which case the first N(NCODA + 1) elements of A will be destroyed.

WK —  Work array of length N.

2.         Informational error

Type   Code

4           1                  The iteration for the eigenvalues failed to converge.

Example

In this example, a DATA statement is used to set A to a matrix given by Gregory and Karney (1969, page 77). The eigenvalues of this matrix are given by

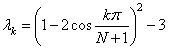
Since the eigenvalues returned by EVLSB are in decreasing magnitude, the above formula for
k = 1, …, N gives the values in a different order. The eigenvalues of this real band symmetric matrix are computed and printed.

 

      USE EVLSB_INT

      USE WRRRN_INT

 

      IMPLICIT   NONE

!                                 Declare variables

      INTEGER    LDA, LDEVEC, N, NCODA

      PARAMETER  (N=5, NCODA=2, LDA=NCODA+1, LDEVEC=N)

!

      REAL       A(LDA,N), EVAL(N)

!                                 Define values of A:

!                                 A = (-1  2  1       )

!                                     ( 2  0  2  1    )

!                                     ( 1  2  0  2  1 )

!                                     (    1  2  0  2 )

!                                     (       1  2 -1 )

!                                 Represented in band symmetric

!                                 form this is:

!                                 A = ( 0  0  1  1  1 )

!                                     ( 0  2  2  2  2 )

!                                     (-1  0  0  0 -1 )

!

      DATA A/0.0, 0.0, -1.0, 0.0, 2.0, 0.0, 1.0, 2.0, 0.0, 1.0, 2.0, &

          0.0, 1.0, 2.0, -1.0/

!

       CALL EVLSB (A, NCODA, EVAL)

!                                 Print results

      CALL WRRRN ('EVAL', EVAL, 1, N, 1)

      END

Output

 

                  EVAL

      1       2       3       4       5

  4.464  -3.000  -2.464  -2.000   1.000

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260