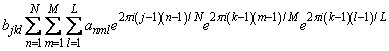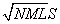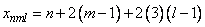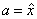FFT3B

Computes the inverse Fourier transform of a complex periodic three-dimensional array.

Required Arguments

A — Three-dimensional complex matrix containing the data to be transformed.   (Input)

B — Three-dimensional complex matrix containing the inverse Fourier coefficients of A.   (Output)
The matrices A and B may be the same.

Optional Arguments

N1 — Limit on the first subscript of matrices A and B.   (Input)
Default: N1 = size (A,1).

N2 — Limit on the second subscript of matrices A and B.   (Input)
Default: N2 = size (A,2).

N3 — Limit on the third subscript of matrices A and B.   (Input)
Default: N3 = size (A,3).

LDA — Leading dimension of A exactly as specified in the dimension statement of the calling program.   (Input)
Default: LDA = size (A,1).

MDA — Middle dimension of A exactly as specified in the dimension statement of the calling program.   (Input)
Default: MDA = size (A,2).

LDB — Leading dimension of B exactly as specified in the dimension statement of the calling program.   (Input)
Default: LDB = size (B,1).

MDB — Middle dimension of B exactly as specified in the dimension statement of the calling program.   (Input)
Default: MDB = size (B,2).

FORTRAN 90 Interface

Generic:          CALL FFT3B (A, B [,…])

Specific:         The specific interface names are S_FFT3B and D_FFT3B.

FORTRAN 77 Interface

Single:            CALL FFT3B (N1, N2, N3, A, LDA, MDA, B, LDB, MDB)

Double:          The double precision name is DFFT3B.

Description

The routine FFT3B computes the inverse discrete complex Fourier transform of a complex three-dimensional array of size (N1 = N) Χ (N2 = M) Χ (N3 = L). The method used is a variant of the Cooley-Tukey algorithm, which is most efficient when N, M, and L are each products of small prime factors. If N, M, and L satisfy this condition, then the computational effort is proportional to N M L log N M L. This considerable savings has historically led people to refer to this algorithm as the “fast Fourier transform” or FFT.

Specifically, given an N ΄ M ΄ L array a, FFT3B returns in b

Furthermore, a vector of Euclidean norm S is mapped into a vector of norm

Finally, note that an unnormalized inverse is implemented in FFT3F. The routine FFT3B is based on the complex FFT in FFTPACK. The package FFTPACK was developed by Paul Swarztrauber at the National Center for Atmospheric Research.

Comments

1.         Workspace may be explicitly provided, if desired, by use of F2T3B/DF2T3B. The reference is:

CALL F2T3B (N1, N2, N3, A, LDA, MDA, B, LDB, MDB, WFF1, WFF2, WFF3, CPY)

The additional arguments are as follows:

WFF1 — Real array of length 4 * N1 + 15 initialized by FFTCI. The initialization depends on N1.   (Input)

WFF2 — Real array of length 4 * N2 + 15 initialized by FFTCI. The initialization depends on N2.   (Input)

WFF3 — Real array of length 4 * N3 + 15 initialized by FFTCI. The initialization depends on N3.   (Input)

CPY — Real array of size 2 * MAX(N1, N2, N3).   (Workspace)

2.         The routine FFT3B is most efficient when N1, N2, and N3 are the product of small primes.

3.         If FFT3F/FFT3B is used repeatedly with the same values for N1, N2 and N3, then use FFTCI to fill WFF1(N = N1), WFF2(N = N2), and WFF3(N = N3). Follow this with repeated calls to F2T3F/F2T3B. This is more efficient than repeated calls to FFT3F/FFT3B.

Example

In this example, we compute the Fourier transform of the 2 ΄ 3 ΄ 4 array

for 1 ≤ n ≤ 2, 1 ≤ m ≤ 3, and 1 ≤ l ≤ 4 using the IMSL routine FFT3F. The result

is then inverted using FFT3B. Note that the result is an array b satisfying b = 2(3)(4)x = 24x. In general, FFT3B is an unnormalized inverse with expansion factor N M L.

 

      USE FFT3B_INT

      USE FFT3F_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

      INTEGER    LDA, LDB, MDA, MDB, NDA, NDB

      PARAMETER  (LDA=2, LDB=2, MDA=3, MDB=3, NDA=4, NDB=4)

!                                 SPECIFICATIONS FOR LOCAL VARIABLES

      INTEGER    I, J, K, L, M, N, N1, N2, N3, NOUT

      COMPLEX    A(LDA,MDA,NDA), B(LDB,MDB,NDB), X(LDB,MDB,NDB)

!                                 SPECIFICATIONS FOR INTRINSICS

      INTRINSIC  CEXP, CMPLX

      COMPLEX    CEXP, CMPLX

!                                 SPECIFICATIONS FOR SUBROUTINES

!                                 Get output unit number

      CALL UMACH (2, NOUT)

      N1 = 2

      N2 = 3

      N3 = 4

!                                 Set array X

      DO 30  N=1, 2

         DO 20  M=1, 3

            DO 10  L=1, 4

               X(N,M,L) = N + 2*(M-1) + 2*3*(L-1)

   10       CONTINUE

   20    CONTINUE

   30 CONTINUE

!

      CALL FFT3F (X, A)

      CALL FFT3B (A, B)

!

      WRITE (NOUT,99996)

      DO 50  I=1, 2

         WRITE (NOUT,99998) I

         DO 40  J=1, 3

            WRITE (NOUT,99999) (X(I,J,K),K=1,4)

   40    CONTINUE

   50 CONTINUE

!

      WRITE (NOUT,99997)

      DO 70  I=1, 2

         WRITE (NOUT,99998) I

         DO 60  J=1, 3

            WRITE (NOUT,99999) (A(I,J,K),K=1,4)

   60    CONTINUE

   70 CONTINUE

!

      WRITE (NOUT, 99995)

      DO 90  I=1, 2

         WRITE (NOUT,99998) I

         DO 80  J=1, 3

            WRITE (NOUT,99999) (B(I,J,K),K=1,4)

   80    CONTINUE

   90 CONTINUE

99995 FORMAT (13X, 'The unnormalized inverse is')

99996 FORMAT (13X, 'The input for FFT3F is')

99997 FORMAT (/, 13X, 'The results from FFT3F are')

99998 FORMAT (/, ' Face no. ', I1)

99999 FORMAT (1X, 4('(',F6.2,',',F6.2,')',3X))

      END

Output

 

            The input for FFT3F is

Face no. 1
(  1.00,  0.00)   (  7.00,  0.00)   ( 13.00,  0.00)   ( 19.00,  0.00)
(  3.00,  0.00)   (  9.00,  0.00)   ( 15.00,  0.00)   ( 21.00,  0.00)
(  5.00,  0.00)   ( 11.00,  0.00)   ( 17.00,  0.00)   ( 23.00,  0.00)

Face no. 2
(  2.00,  0.00)   (  8.00,  0.00)   ( 14.00,  0.00)   ( 20.00,  0.00)
(  4.00,  0.00)   ( 10.00,  0.00)   ( 16.00,  0.00)   ( 22.00,  0.00)
(  6.00,  0.00)   ( 12.00,  0.00)   ( 18.00,  0.00)   ( 24.00,  0.00)

The results from FFT3F are

Face no. 1
(300.00,  0.00)   (-72.00, 72.00)   (-72.00,  0.00)   (-72.00,-72.00)
(-24.00, 13.86)   (  0.00,  0.00)   (  0.00,  0.00)   (  0.00,  0.00)
(-24.00,-13.86)   (  0.00,  0.00)   (  0.00,  0.00)   (  0.00,  0.00)

Face no. 2
(-12.00,  0.00)   (  0.00,  0.00)   (  0.00,  0.00)   (  0.00,  0.00)
(  0.00,  0.00)   (  0.00,  0.00)   (  0.00,  0.00)   (  0.00,  0.00)
(  0.00,  0.00)   (  0.00,  0.00)   (  0.00,  0.00)   (  0.00,  0.00)

The unnormalized inverse is

Face no. 1
( 24.00,  0.00)   (168.00,  0.00)   (312.00,  0.00)   (456.00,  0.00)
( 72.00,  0.00)   (216.00,  0.00)   (360.00,  0.00)   (504.00,  0.00)
(120.00,  0.00)   (264.00,  0.00)   (408.00,  0.00)   (552.00,  0.00)

Face no. 2
( 48.00,  0.00)   (192.00,  0.00)   (336.00,  0.00)   (480.00,  0.00)
( 96.00,  0.00)   (240.00,  0.00)   (384.00,  0.00)   (528.00,  0.00)
(144.00,  0.00)   (288.00,  0.00)   (432.00,  0.00)   (576.00,  0.00)

Visual Numerics, Inc.
Visual Numerics - Developers of IMSL and PV-WAVE
http://www.vni.com/
PHONE: 713.784.3131
FAX:713.781.9260