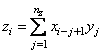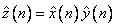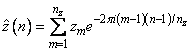RCONV

Chapter 6: Transforms

RCONV

Computes the convolution of two real vectors .

Required Arguments

X — Real vector of length NX. (Input)

Y — Real vector of length NY. (Input)

Z — Real vector of length NZ ontaining the convolution of X and Y. (Output)

ZHAT — Real vector of length NZ containing the discrete Fourier transform of Z. (Output)

Optional Arguments

IDO — Flag indicating the usage of RCONV. (Input)
Default: IDO = 0.

IDO Usage

0 If this is the only call to RCONV.

If RCONV is called multiple times in sequence with the same NX, NY, and IPAD, IDO should be set to

1 on the first call

2 on the intermediate calls

3 on the final call.

NX — Length of the vector X. (Input)
Default: NX = size (X,1).

NY — Length of the vector Y. (Input)
Default: NY = size (Y,1).

IPAD — IPAD should be set to zero for periodic data or to one for nonperiodic data. (Input)
Default: IPAD = 0.

NZ — Length of the vector Z. (Input/Output)
Upon input: When IPAD is zero, NZ must be at least MAX(NX, NY). When IPAD is one, NZ must be greater than or equal to the smallest integer greater than or equal to
(NX + NY -1) of the form (2α) * (3β) * (5γ) where alpha, beta, and gamma are nonnegative integers. Upon output, the value for NZ that was used by RCONV.
Default: NZ = size (Z,1).

FORTRAN 90 Interface

Generic: CALL RCONV (X, Y, Z, ZHAT [,…])

Specific: The specific interface names are S_RCONV and D_RCONV.

FORTRAN 77 Interface

Single: CALL RCONV (IDO, NX, X, NY, Y, IPAD, NZ, Z, ZHAT)

Double: The double precision name is DRCONV.

Description

The routine RCONV computes the discrete convolution of two sequences x and y. More precisely, let nx be the length of x and ny denote the length of y. If a circular convolution is desired, then IPAD must be set to zero. We set

nz := max{nx, ny}

and we pad out the shorter vector with zeroes. Then, we compute

where the index on x is interpreted as a positive number between 1 and nz, modulo nz.

The technique used to compute the zi's is based on the fact that the (complex discrete) Fourier transform maps convolution into multiplication. Thus, the Fourier transform of z is given by

where

The technique used here to compute the convolution is to take the discrete Fourier transform of x and y, multiply the results together component-wise, and then take the inverse transform of this product. It is very important to make sure that nz is a product of small primes if IPAD is set to zero. If nz is a product of small primes, then the computational effort will be proportional to nz log(nz). If IPAD is one, then a good value is chosen for nz so that the Fourier transforms are efficient and
nz ≥ nx + ny - 1. This will mean that both vectors will be padded with zeroes.

We point out that no complex transforms of x or y are taken since both sequences are real, we can take real transforms and simulate the complex transform above. This can produce a savings of a factor of six in time as well as save space over using the complex transform.

Comments

1. Workspace may be explicitly provided, if desired, by use of R2ONV/DR2ONV. The reference is:

CALL R2ONV (IDO, NX, X, NY, Y, IPAD, NZ, Z, ZHAT, XWK, YWK, WK)

The additional arguments are as follows:

XWK — Real work array of length NZ.

YWK — Real work array of length NZ.

WK — Real work arrary of length 2 * NZ + 15.

2. Informational error
Type Code

4 1 The length of the vector Z must be large enough to hold the results. An acceptable length is returned in NZ.

Example

In this example, we compute both a periodic and a non-periodic convolution. The idea here is that one can compute a moving average of the type found in digital filtering using this routine. The averaging operator in this case is especially simple and is given by averaging five consecutive points in the sequence. The periodic case tries to recover a noisy sin function by averaging five nearby values. The nonperiodic case tries to recover the values of an exponential function contaminated by noise. The large error for the last value printed has to do with the fact that the convolution is averaging the zeroes in the “pad” rather than function values. Notice that the signal size is 100, but we only report the errors at ten points.

USE IMSL_LIBRARIES

IMPLICIT NONE

INTEGER NFLTR, NY, A

PARAMETER (NFLTR=5, NY=100)

INTEGER I, IPAD, K, MOD, NOUT, NZ

REAL ABS, EXP, F1, F2, FLOAT, FLTR(NFLTR), &

FLTRER, ORIGER, SIN, TOTAL1, TOTAL2, TWOPI, X, &

Y(NY), Z(2*(NFLTR+NY-1)), ZHAT(2*(NFLTR+NY-1))

INTRINSIC ABS, EXP, FLOAT, MOD, SIN

! DEFINE FUNCTIONS

F1(X) = SIN(X)

F2(X) = EXP(X)

CALL RNSET (1234579)

CALL UMACH (2, NOUT)

TWOPI = CONST('PI')

TWOPI = 2.0*TWOPI

! SET UP THE FILTER

DO 10 I=1, 5

FLTR(I) = 0.2

10 CONTINUE

! SET UP Y-VECTOR FOR THE PERIODIC

! CASE.

DO 20 I=1, NY

X = TWOPI*FLOAT(I-1)/FLOAT(NY-1)

Y(I) = RNUNF()

Y(I) = F1(X) + 0.5*Y(I) - 0.25

20 CONTINUE

! CALL THE CONVOLUTION ROUTINE FOR THE

! PERIODIC CASE.

NZ = 2*(NFLTR+NY-1)

CALL RCONV (FLTR, Y, Z, ZHAT, IPAD=0, NZ=NZ)

! PRINT RESULTS

WRITE (NOUT,99993)

WRITE (NOUT,99995)

TOTAL1 = 0.0

TOTAL2 = 0.0

DO 30 I=1, NY

! COMPUTE THE OFFSET FOR THE Z-VECTOR

IF (I .GE. NY-1) THEN

K = I - NY + 2

ELSE

K = I + 2

END IF

X = TWOPI*FLOAT(I-1)/FLOAT(NY-1)

ORIGER = ABS(Y(I)-F1(X))

FLTRER = ABS(Z(K)-F1(X))

IF (MOD(I,11) .EQ. 1) WRITE (NOUT,99997) X, F1(X), ORIGER, &

FLTRER

TOTAL1 = TOTAL1 + ORIGER

TOTAL2 = TOTAL2 + FLTRER

30 CONTINUE

WRITE (NOUT,99998) TOTAL1/FLOAT(NY)

WRITE (NOUT,99999) TOTAL2/FLOAT(NY)

! SET UP Y-VECTOR FOR THE NONPERIODIC

! CASE.

DO 40 I=1, NY

A = FLOAT(I-1)/FLOAT(NY-1)

Y(I) = RNUNF()

Y(I) = F2(A) + 0.5*Y(I) - 0.25

40 CONTINUE

! CALL THE CONVOLUTION ROUTINE FOR THE

! NONPERIODIC CASE.

NZ = 2*(NFLTR+NY-1)

CALL RCONV (FLTR, Y, Z, ZHAT, IPAD=1)

! PRINT RESULTS

WRITE (NOUT,99994)

WRITE (NOUT,99996)

TOTAL1 = 0.0

TOTAL2 = 0.0

DO 50 I=1, NY

X = FLOAT(I-1)/FLOAT(NY-1)

ORIGER = ABS(Y(I)-F2(X))

FLTRER = ABS(Z(I+2)-F2(X))

IF (MOD(I,11) .EQ. 1) WRITE (NOUT,99997) X, F2(X), ORIGER, &

FLTRER

TOTAL1 = TOTAL1 + ORIGER

TOTAL2 = TOTAL2 + FLTRER

50 CONTINUE

WRITE (NOUT,99998) TOTAL1/FLOAT(NY)

WRITE (NOUT,99999) TOTAL2/FLOAT(NY)

99993 FORMAT (' Periodic Case')

99994 FORMAT (/,' Nonperiodic Case')

99995 FORMAT (8X, 'x', 9X, 'sin(x)', 6X, 'Original Error', 5X, &

'Filtered Error')

99996 FORMAT (8X, 'x', 9X, 'exp(x)', 6X, 'Original Error', 5X, &

'Filtered Error')

99997 FORMAT (1X, F10.4, F13.4, 2F18.4)

99998 FORMAT (' Average absolute error before filter:', F10.5)

99999 FORMAT (' Average absolute error after filter:', F11.5)

END

Output

Periodic Case
    x         sin(x)      Original Error     Filtered Error
0.0000       0.0000            0.0811            0.0587
0.6981       0.6428            0.0226            0.0781
1.3963       0.9848            0.1526            0.0529
2.0944       0.8660            0.0959            0.0125
2.7925       0.3420            0.1747            0.0292
3.4907      -0.3420            0.1035            0.0238
4.1888      -0.8660            0.0402            0.0595
4.8869      -0.9848            0.0673            0.0798
5.5851      -0.6428            0.1044            0.0074
6.2832       0.0000            0.0154            0.0018
Average absolute error before filter:   0.12481
Average absolute error after filter:    0.04778

Nonperiodic Case
    x         exp(x)      Original Error     Filtered Error
0.0000       1.0000            0.1476            0.3915
0.1111       1.1175            0.0537            0.0326
0.2222       1.2488            0.1278            0.0932
0.3333       1.3956            0.1136            0.0987
0.4444       1.5596            0.1617            0.0964
0.5556       1.7429            0.0071            0.0662
0.6667       1.9477            0.1248            0.0713
0.7778       2.1766            0.1556            0.0158
0.8889       2.4324            0.1529            0.0696
1.0000       2.7183            0.2124            1.0562
Average absolute error before filter:   0.12538
Average absolute error after filter:    0.07764

Visual Numerics, Inc.
Visual Numerics - Developers of IMSL and PV-WAVE
http://www.vni.com/
PHONE: 713.784.3131
FAX:713.781.9260