Uses the Generalized Minimal Residual Method with reverse communication to generate an approximate solution of Ax = b.
Required Arguments
IDO— Flag indicating task to be
done. (Input/Output)
On the initial call IDO must be 0. If the
routine returns with IDO = 1, then set
Z = AP, where A is the matrix, and call GMRES again. If the
routine returns with IDO = 2, then set
Z to the solution of the system MZ = P, where M is
the preconditioning matrix, and call GMRES again. If the
routine returns with IDO = 3, set
Z =
AM-1P, and call GMRES again. If the
routine returns with IDO = 4, the
iteration has converged, and X contains the
approximate solution to the linear system.
X — Array of length N containing an
approximate solution. (Input/Output)
On input, X contains an initial
guess of the solution. On output, X contains the
approximate solution.
P — Array of length N.
(Output)
Its use is described under IDO.
R — Array of length N.
(Input/Output)
On initial input, it contains the right-hand side of the
linear system. On output, it contains the residual, b − Ax.
Z — Array of length N.
(Input)
When IDO = 1, it contains
AP, where A is the coefficient matrix. When IDO = 2, it contains
M-1P. When IDO = 3, it contains
AM-1P. When IDO = 0, it is
ignored.
TOL — Stopping tolerance.
(Input/Output)
The algorithm attempts to generate a solution x such
that |b −
Ax| ≤ TOL*|b|. On
output, TOL
contains the final residual norm.
Optional Arguments
N — Order of the linear system.
(Input)
Default: N = size (X,1).
FORTRAN 90 Interface
Generic: CALL GMRES (IDO, X, P, R, Z, TOL [,…])
Specific: The specific interface names are S_GMRES and D_GMRES.
FORTRAN 77 Interface
Single: CALL GMRES (IDO, N, X, P, R, Z, TOL)
Double: The double precision name is DGMRES.
Description
The routine GMRES implements restarted GMRES with reverse communication to generate an approximate solution to Ax = b. It is based on GMRESD by Homer Walker.
There are four distinct GMRES implementations, selectable through the parameter vector INFO. The first Gram-Schmidt implementation, INFO(1) = 1, is essentially the original algorithm by Saad and Schultz (1986). The second Gram-Schmidt implementation, developed by Homer Walker and Lou Zhou, is simpler than the first implementation. The least squares problem is constructed in upper-triangular form and the residual vector updating at the end of a GMRES cycle is cheaper. The first Householder implementation is algorithm 2.2 of Walker (1988), but with more efficient correction accumulation at the end of each GMRES cycle. The second Householder implementation is algorithm 3.1 of Walker (1988). The products of Householder transformations are expanded as sums, allowing most work to be formulated as large scale matrix-vector operations. Although BLAS are used wherever possible, extensive use of Level 2 BLAS in the second Householder implementation may yield a performance advantage on certain computing environments.
The Gram-Schmidt implementations are less expensive than the Householder, the latter requiring about twice as much arithmetic beyond the coefficient matrix/vector products. However, the Householder implementations may be more reliable near the limits of residual reduction. See Walker (1988) for details. Issues such as the cost of coefficient matrix/vector products, availability of effective preconditioners, and features of particular computing environments may serve to mitigate the extra expense of the Householder implementations.
Comments
1. Workspace may be explicitly provided, if desired, by use of G2RES/DG2RES. The reference is:
CALL G2RES (IDO, N, X, P, R, Z, TOL, INFO, USRNPR, USRNRM, WORK)
The additional arguments are as follows:
INFO — Integer vector of length 10 used to change parameters of GMRES. (Input/Output).
For any components INFO(1) ... INFO(7) with value zero on input, the default value is used.
INFO(1) = IMP, the flag indicating the desired implementation.
|
IMP |
Action |
|
1 |
first Gram-Schmidt implementation |
|
2 |
second Gram-Schmidt implementation |
|
3 |
first Householder implementation |
|
4 |
second Householder implementation |
Default: IMP = 1
INFO(2) = KDMAX, the maximum
Krylor subspace dimension, i.e., the maximum allowable number of GMRES iterations
before restarting. It must satisfy 1 ≤ KDMAX ≤ N.
Default: KDMAX = min(N, 20)
INFO(3) = ITMAX, the maximum
number of GMRES
iterations allowed.
Default: ITMAX = 1000
INFO(4) = IRP, the flag
indicating whether right preconditioning is used.
If IRP = 0, no right
preconditioning is performed. If IRP = 1, right
preconditioning is performed. If IRP = 0, then IDO = 2 or 3 will not
occur.
Default: IRP = 0
INFO(5) = IRESUP, the flag that indicates the desired residual vector updating prior to restarting or on termination.
|
IRESUP |
Action |
|
1 |
update by linear combination, restarting only |
|
2 |
update by linear combination, restarting and termination |
|
3 |
update by direct evaluation, restarting only |
|
4 |
update by direct evaluation, restarting and termination |
Updating by direct evaluation requires an otherwise unnecessary matrix-vector product. The alternative is to update by forming a linear combination of various available vectors. This may or may not be cheaper and may be less reliable if the residual vector has been greatly reduced. If IRESUP = 2 or 4, then the residual vector is returned in WORK(1), ..., WORK(N). This is useful in some applications but costs another unnecessary residual update. It is recommended that IRESUP = 1 or 2 be used, unless matrix-vector products are inexpensive or great residual reduction is required. In this case use IRESUP = 3 or 4. The meaning of “inexpensive” varies with IMP as follows:
|
IMP |
≤ |
|
1 |
(KDMAX + 1) *N flops |
|
2 |
N flops |
|
3 |
(2*KDMAX + 1) *N flops |
|
4 |
(2*KDMAX + 1) *N flops |
“Great residual reduction” means that TOL is only a few
orders of magnitude larger than machine epsilon.
Default: IRESUP = 1
INFO(6) = flag for
indicating the inner product and norm used in the Gram-Schmidt implementations.
If INFO(6) = 0,
sdot and snrm2, from BLAS, are
used. If INFO(6)
= 1, the user must provide the routines, as specified under arguments USRNPR and USRNRM.
Default:
INFO(6) = 0
INFO(7) = IPRINT, the print
flag. If IPRINT
= 0, no printing is performed. If
IPRINT = 1, print the
iteration numbers and residuals.
Default: IPRINT = 0
INFO(8) = the total number of GMRES iterations on output.
INFO(9) = the total number of matrix-vector products in GMRES on output.
INFO(10) = the total number of right preconditioner solves in GMRES on output if IRP = 1.
USRNPR — User-supplied FUNCTION to use as the inner product in the Gram-Schmidt implementation, if INFO(6) = 1. If INFO(6) = 0, the dummy function G8RES/DG8RES may be used. The usage is
REAL FUNCTION USRNPR (N, SX, INCX, SY, INCY)
N — Length of vectors X and Y. (Input)
SX — Real vector of length MAX(N*IABS(INCX),1). (Input)
INCX — Displacement
between elements of SX.
(Input)
X(I) is defined to be
SX(1+(I-1)*INCX)
if INCX is
greater than 0, or
SX(1+(I-N)*INCX) if
INCX is less
than 0.
SY — Real vector of length MAX(N*IABS(INXY),1). (Input)
INCY — Displacement
between elements of SY.
(Input)
Y(I)
is defined to be SY(1+(I-1)*INCY) if
INCY is greater
than 0, or
SY(1+(I-N)*INCY) if
INCY is less
than zero.
USRNPR must be
declared EXTERNAL in the
calling program.
USRNRM — User-supplied FUNCTION to use as the norm ||X|| in the Gram-Schmidt implementation, if INFO(6) = 1. If INFO(6) = 0, the dummy function G9RES/DG9RES may be used.The usage is
REAL FUNCTION USRNRM (N, SX, INCX)
N — Length of vectors X and Y. (Input)
SX — Real vector of length MAX(N*IABS(INCX),1). (Input)
INCX — Displacement
between elements of SX.
(Input)
X(I)
is defined to be SX(1+(I-1)*INCX) if
INCX is greater
than 0, or
SX(1+(I-N)*INCX) if
INCX is less
than 0.
USRNRM must be
declared EXTERNAL in the
calling program.
WORK — Work array whose length is dependent on the chosen implementation.
|
IMP |
length of WORK |
|
1 |
N*(KDMAX + 2) + KDMAX**2 + 3 *KDMAX + 2 |
|
2 |
N*(KDMAX + 2) + KDMAX**2 + 2 *KDMAX + 1 |
|
3 |
N*(KDMAX + 2) + 3 *KDMAX + 2 |
|
4 |
N*(KDMAX + 2) + KDMAX**2 + 2 *KDMAX + 2 |
Example 1
This is a simple example of GMRES usage. A solution to a small linear system is found. The coefficient matrix A is stored as a full matrix, and no preconditioning is used. Typically, preconditioning is required to achieve convergence in a reasonable number of iterations.
USE IMSL_LIBRARIES
! Declare variables
INTEGER LDA, N
PARAMETER (N=3, LDA=N)
! Specifications for local variables
INTEGER IDO, NOUT
REAL P(N), TOL, X(N), Z(N)
REAL A(LDA,N), R(N)
SAVE A, R
! Specifications for intrinsics
INTRINSIC SQRT
REAL SQRT
! ( 33.0 16.0 72.0)
! A = (-24.0 -10.0 -57.0)
! ( 18.0 -11.0 7.0)
!
! B = (129.0 -96.0 8.5)
!
DATA A/33.0, -24.0, 18.0, 16.0, -10.0, -11.0, 72.0, -57.0, 7.0/
DATA R/129.0, -96.0, 8.5/
!
CALL UMACH (2, NOUT)
!
! Initial guess = (0 ... 0)
!
X = 0.0E0
! Set stopping tolerance to
! square root of machine epsilon
TOL =
AMACH(4)
TOL = SQRT(TOL)
IDO = 0
10 CONTINUE
CALL GMRES (IDO, X, P, R, Z, TOL)
IF (IDO .EQ. 1) THEN
! Set z = A*p
CALL MURRV (A, P, Z)
GO TO 10
END IF
!
CALL WRRRN ('Solution', X, 1, N, 1)
WRITE (NOUT,'(A11, E15.5)') 'Residual = ', TOL
END
Output
Solution
1 2
3
1.000 1.500 1.000
Residual
= 0.29746E-05
Additional Examples
Example 2
This example solves a linear system with a coefficient matrix stored in coordinate form, the same problem as in the document example for LSLXG. Jacobi preconditioning is used, i.e. the preconditioning matrix M is the diagonal matrix with Mii = Aii, for i = 1, …, n.
USE IMSL_LIBRARIES
INTEGER N, NZ
PARAMETER (N=6, NZ=15)
! Specifications for local variables
INTEGER IDO, INFO(10), NOUT
REAL P(N), TOL, WORK(1000), X(N), Z(N)
REAL DIAGIN(N), R(N)
! Specifications for intrinsics
INTRINSIC SQRT
REAL SQRT
! Specifications for subroutines
EXTERNAL
AMULTP
!
Specifications for functions
EXTERNAL G8RES, G9RES
!
DATA DIAGIN/0.1, 0.1, 0.0666667, 0.1, 1.0, 0.16666667/
DATA R/10.0, 7.0, 45.0, 33.0, -34.0, 31.0/
!
CALL UMACH (2, NOUT)
! Initial guess = (1 ... 1)
X = 1.0E0
! Set up the options vector INFO
! to use preconditioning
INFO = 0
INFO(4) = 1
! Set stopping tolerance to
! square root of machine epsilon
TOL = AMACH(4)
TOL = SQRT(TOL)
IDO = 0
10 CONTINUE
CALL G2RES (IDO, N, X, P, R, Z, TOL, INFO, G8RES, G9RES, WORK)
IF (IDO .EQ. 1) THEN
! Set z = A*p
CALL AMULTP (P, Z)
GO TO 10
ELSE IF (IDO .EQ. 2) THEN
!
! Set z = inv(M)*p
! The diagonal of inv(M) is stored
! in DIAGIN
!
CALL SHPROD (N, DIAGIN, 1, P, 1, Z, 1)
GO TO 10
ELSE IF (IDO .EQ. 3) THEN
!
! Set z = A*inv(M)*p
!
CALL SHPROD (N, DIAGIN, 1, P, 1, Z, 1)
P = Z
CALL AMULTP (P, Z)
GO TO 10
END IF
!
CALL WRRRN ('Solution', X)
WRITE (NOUT,'(A11, E15.5)') 'Residual = ', TOL
END
!
SUBROUTINE AMULTP (P, Z)
USE IMSL_LIBRARIES
INTEGER NZ
PARAMETER (NZ=15)
! SPECIFICATIONS FOR ARGUMENTS
REAL P(*), Z(*)
! SPECIFICATIONS FOR PARAMETERS
INTEGER N
PARAMETER (N=6)
! SPECIFICATIONS FOR LOCAL VARIABLES
INTEGER I
INTEGER IROW(NZ), JCOL(NZ)
REAL A(NZ)
SAVE A, IROW, JCOL
! SPECIFICATIONS FOR SUBROUTINES
! Define the matrix A
!
DATA A/6.0, 10.0, 15.0, -3.0, 10.0, -1.0, -1.0, -3.0, -5.0, 1.0, &
10.0, -1.0, -2.0, -1.0, -2.0/
DATA IROW/6, 2, 3, 2, 4, 4, 5, 5, 5, 5, 1, 6, 6, 2, 4/
DATA JCOL/6, 2, 3, 3, 4, 5, 1, 6, 4, 5, 1, 1, 2, 4, 1/
!
CALL SSET(N, 0.0, Z, 1)
! Accumulate the product A*p in z
DO 10 I=1, NZ
Z(IROW(I)) = Z(IROW(I)) + A(I)*P(JCOL(I))
10 CONTINUE
RETURN
END
Output
Solution
1 1.000
2 2.000
3 3.000
4 4.000
5 5.000
6 6.000
Residual = 0.25882E-05
Example 3
The coefficient matrix in this example corresponds to the five-point discretization of the 2-d Poisson equation with the Dirichlet boundary condition. Assuming the natural ordering of the unknowns, and moving all boundary terms to the right hand side, we obtain the block tridiagonal matrix
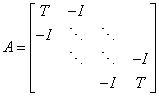
where
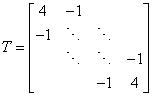
and I is the identity matrix. Discretizing on a k × k grid implies that T and I are both k × k, and thus the coefficient matrix A is k2 × k2.
The problem is solved twice, with discretization on a 50 × 50 grid. During both solutions, use the second Householder implementation to take advantage of the large scale matrix/vector operations done in Level 2 BLAS. Also choose to update the residual vector by direct evaluation since the small tolerance will require large residual reduction.
The first solution uses no preconditioning. For the second solution, we construct a block diagonal preconditioning matrix
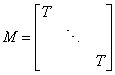
M is factored once, and these factors are used in the forward solves and back substitutions necessary when GMRES returns with IDO = 2 or 3.
Timings are obtained for both solutions, and the ratio of the time for the solution with no preconditioning to the time for the solution with preconditioning is printed. Though the exact results are machine dependent, we see that the savings realized by faster convergence from using a preconditioner exceed the cost of factoring M and performing repeated forward and back solves.
USE
IMSL_LIBRARIES
INTEGER K,
N
PARAMETER (K=50, N=K*K)
! Specifications for local variables
INTEGER IDO, INFO(10), IR(20), IS(20), NOUT
REAL A(2*N), B(2*N), C(2*N), G8RES, G9RES, P(2*N), R(N), &
TNOPRE, TOL, TPRE, U(2*N), WORK(100000), X(N), &
Y(2*N), Z(2*N)
! Specifications for subroutines
EXTERNAL AMULTP,
G8RES,
G9RES
!
Specifications for functions
CALL UMACH (2, NOUT)
! Right hand side and initial guess
! to (1 ... 1)
R =
1.0E0
X = 1.0E0
! Use the 2nd Householder
! implementation and update the
! residual by direct evaluation
INFO = 0
INFO(1) = 4
INFO(5) = 3
TOL = AMACH(4)
TOL = 100.0*TOL
IDO = 0
! Time the solution with no
! preconditioning
TNOPRE = CPSEC()
10 CONTINUE
CALL G2RES (IDO, N, X, P, R, Z, TOL, INFO, G8RES, G9RES, WORK)
IF (IDO .EQ. 1) THEN
!
! Set z = A*p
!
CALL AMULTP (K, P, Z)
GO TO 10
END IF
TNOPRE = CPSEC() - TNOPRE
!
WRITE (NOUT,'(A32, I4)') 'Iterations, no preconditioner = ', &
INFO(8)
!
! Solve again using the diagonal blocks
! of A as the preconditioning matrix M
R =
1.0E0
X = 1.0E0
! Define M
CALL SSET (N-1, -1.0, B, 1)
CALL SSET (N-1, -1.0, C, 1)
CALL SSET (N, 4.0, A, 1)
INFO(4) = 1
TOL = AMACH(4)
TOL = 100.0*TOL
IDO = 0
TPRE = CPSEC()
! Compute the LDU factorization of M
!
CALL LSLCR (C, A, B, Y, U, IR, IS, IJOB=6)
20 CONTINUE
CALL G2RES (IDO, N, X, P, R, Z, TOL, INFO, G8RES, G9RES, WORK)
IF (IDO .EQ. 1) THEN
!
! Set z = A*p
!
CALL AMULTP (K, P, Z)
GO TO 20
ELSE IF (IDO .EQ. 2) THEN
!
! Set z = inv(M)*p
!
CALL SCOPY (N, P, 1, Z, 1)
CALL LSLCR (C, A, B, Z, U, IR, IS, IJOB=5)
GO TO 20
ELSE IF (IDO .EQ. 3) THEN
!
! Set z = A*inv(M)*p
!
CALL LSLCR (C, A, B, P, U, IR, IS, IJOB=5)
CALL AMULTP (K, P, Z)
GO TO 20
END IF
TPRE = CPSEC() - TPRE
WRITE (NOUT,'(A35, I4)') 'Iterations, with preconditioning = ',&
INFO(8)
WRITE (NOUT,'(A45, F10.5)') '(Precondition time)/(No '// &
'precondition time) = ', TPRE/TNOPRE
!
END
!
SUBROUTINE AMULTP (K, P,
Z)
USE IMSL_LIBRARIES
! Specifications for arguments
INTEGER K
REAL P(*), Z(*)
! Specifications for local variables
INTEGER I, N
!
N = K*K
! Multiply by diagonal blocks
!
CALL SVCAL (N, 4.0, P, 1, Z, 1)
CALL SAXPY (N-1, -1.0, P(2:(N)), 1, Z, 1)
CALL SAXPY (N-1, -1.0, P, 1, Z(2:(N)), 1)
!
! Correct for terms not properly in
! block diagonal
DO 10 I=K, N - K, K
Z(I) = Z(I) + P(I+1)
Z(I+1) = Z(I+1) + P(I)
10 CONTINUE
! Do the super and subdiagonal blocks,
! the -I's
!
CALL SAXPY (N-K, -1.0, P((K+1):(N)), 1, Z, 1)
CALL SAXPY (N-K, -1.0, P, 1, Z((K+1):(N)), 1)
!
RETURN
END
Output
Iterations, no preconditioner = 329
Iterations, with preconditioning = 192
(Precondition time)/(No precondition time) = 0.66278
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |