LSQRR

Solves a linear least-squares problem without iterative refinement.

Required Arguments

A — NRA by NCA matrix containing the coefficient matrix of the least-squares system to be solved. (Input)

B — Vector of length NRA containing the right-hand side of the least-squares system. (Input)

X — Vector of length NCA containing the solution vector with components corresponding to the columns not used set to zero. (Output)

RES — Vector of length NRA containing the residual vector B − A * X. (Output)

KBASIS — Scalar containing the number of columns used in the solution.

Optional Arguments

NRA — Number of rows of A. (Input)
Default: NRA = size (A,1).

NCA — Number of columns of A. (Input)
Default: NCA = size (A,2).

LDA — Leading dimension of A exactly as specified in the dimension statement of the calling program. (Input)
Default: LDA = size (A,1).

TOL — Scalar containing the nonnegative tolerance used to determine the subset of columns of A to be included in the solution. (Input)
If TOL is zero, a full complement of min(NRA, NCA) columns is used. See Comments.
Default: TOL = 0.0

FORTRAN 90 Interface

Generic: CALL LSQRR (A, B, X, RES, KBASIS [,…])

Specific: The specific interface names are S_LSQRR and D_LSQRR.

FORTRAN 77 Interface

Single: CALL LSQRR (NRA, NCA, A, LDA, B, TOL, X, RES, KBASIS)

Double: The double precision name is DLSQRR.

ScaLAPACK Interface

Generic: CALL LSQRR (A0, B0, X0, RES0, KBASIS [,…])

Specific: The specific interface names are S_LSQRR and D_LSQRR.

See the ScaLAPACK Usage Notes below for a description of the arguments for distributed computing.

Description

Routine LSQRR solves the linear least-squares problem. The underlying code is based on either LINPACK , LAPACK, or ScaLAPACK code depending upon which supporting libraries are used during linking. For a detailed explanation see “Using ScaLAPACK, LAPACK, LINPACK, and EISPACK” in the Introduction section of this manual. The routine LQRRR is first used to compute the QR decomposition of A. Pivoting, with all rows free, is used. Column k is in the basis if

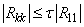
with τ = TOL. The truncated least-squares problem is then solved using IMSL routine LQRSL. Finally, the components in the solution, with the same index as columns that are not in the basis, are set to zero; and then, the permutation determined by the pivoting in IMSL routine LQRRR is applied.

Comments

1. Workspace may be explicitly provided, if desired, by use of L2QRR/DL2QRR. The reference is:

CALL L2QRR (NRA, NCA, A, LDA, B, TOL, X, RES, KBASIS, QR,
QRAUX, IPVT, WORK)

The additional arguments are as follows:

QR — Work vector of length NRA * NCA representing an NRA by NCA matrix that contains information from the QR factorization of A. The upper trapezoidal part of QR contains the upper trapezoidal part of R with its diagonal elements ordered in decreasing magnitude. The strict lower trapezoidal part of QR contains information to recover the orthogonal matrix Q of the factorization. If A is not needed, QR can share the same storage locations as A.

QRAUX — Work vector of length NCA containing information about the orthogonal factor of the QR factorization of A.

IPVT — Integer work vector of length NCA containing the pivoting information for the QR factorization of A.

WORK — Work vector of length 2 * NCA − 1.

2. Routine LSQRR calculates the QR decomposition with pivoting of a matrix A and tests the diagonal elements against a user-supplied tolerance TOL. The first integer
KBASIS = k is determined for which

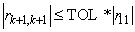
In effect, this condition implies that a set of columns with a condition number approximately bounded by 1.0/TOL is used. Then, LQRSL performs a truncated fit of the first KBASIS columns of the permuted A to an input vector B. The coefficient of this fit is unscrambled to correspond to the original columns of A, and the coefficients corresponding to unused columns are set to zero. It may be helpful to scale the rows and columns of A so that the error estimates in the elements of the scaled matrix are roughly equal to TOL.

3. Integer Options with Chapter 11 Options Manager

16 This option uses four values to solve memory bank conflict (access inefficiency) problems. In routine L2QRR the leading dimension of QR is increased by IVAL(3) when N is a multiple of IVAL(4). The values IVAL(3) and IVAL(4) are temporarily replaced by IVAL(1) and IVAL(2), respectively, in LSQRR. Additional memory allocation for QR and option value restoration are done automatically in LSQRR. Users directly calling L2QRR can allocate additional space for QR and set IVAL(3) and IVAL(4) so that memory bank conflicts no longer cause inefficiencies. There is no requirement that users change existing applications that use LSQRR or L2QRR. Default values for the option are
IVAL(*) = 1, 16, 0, 1.

17 This option has two values that determine if the L1 condition number is to be computed. Routine LSQRR temporarily replaces IVAL(2) by IVAL(1). The routine L2CRG computes the condition number if IVAL(2) = 2. Otherwise L2CRG skips this computation. LSQRR restores the option. Default values for the option are IVAL(*) = 1, 2.

ScaLAPACK Usage Notes

The arguments which differ from the standard version of this routine are:

A0 — MXLDA by MXCOL local matrix containing the local portions of the distributed matrix A. A contains the coefficient matrix of the least squares system to be solved. (Input)

B0 — Local vector of length MXLDA containing the local portions of the distributed vector B. B contains the right-hand side of the least squares system. (Input)

X0 — Local vector of length MXLDX containing the local portions of the distributed vector X. X contains the solution vector with components corresponding to the columns not used set to zero. (Output)

RES0 — Local vector of length MXLDA containing the local portions of the distributed vector RES. RES contains the residual vector B – A * X. (Output)

All other arguments are global and are the same as described for the standard version of the routine. In the argument descriptions above, MXLDA, MXLDX, and MXCOL can be obtained through a call to SCALAPACK_GETDIM (see Utilities) after a call to SCALAPACK_SETUP (see Utilities) has been made. See the ScaLAPACK Example below.

Example

Consider the problem of finding the coefficients ci in

f(x) = c0 + c1x + c2x2

      USE LSQRR_INT
      USE UMACH_INT
      USE WRRRN_INT

! Declare variables

PARAMETER (NRA=4, NCA=3, LDA=NRA)

REAL A(LDA,NCA), B(NRA), X(NCA), RES(NRA), TOL

! Set values for A

! A = ( 1 2 4 )

! ( 1 4 16 )

! ( 1 6 36 )

! ( 1 8 64 )

DATA A/4*1.0, 2.0, 4.0, 6.0, 8.0, 4.0, 16.0, 36.0, 64.0/

! Set values for B

DATA B/ 4.999, 9.001, 12.999, 17.001 /

! Solve the least squares problem

TOL = 1.0E-4

CALL LSQRR (A, B, X, RES, KBASIS, TOL=TOL)

! Print results

CALL UMACH (2, NOUT)

WRITE (NOUT,*) 'KBASIS = ', KBASIS

CALL WRRRN ('X', X, 1, NCA, 1)

CALL WRRRN ('RES', RES, 1, NRA, 1)

END

Output

KBASIS = 3

1 2 3

0.999 2.000 0.000

RES

1 2 3 4

-0.000400 0.001200 -0.001200 0.000400

ScaLAPACK Example

The previous example is repeated here as a distributed computing example. Consider the problem of finding the coefficients ci in

f(x) = c0 + c1x + c2x2

given data at x = 1, 2, 3 and 4, using the method of least squares. The row of the matrix A contains the value of 1, x and x2 at the data points. The vector b contains the data, chosen such that
c0 ≈ 1, c1 ≈ 2 and c2 ≈ 0. The routine LSQRR solves this least-squares problem. SCALAPACK_MAP and SCALAPACK_UNMAP are IMSL utility routines (see Utilities) used to map and unmap arrays to and from the processor grid. They are used here for brevity. DESCINIT is a ScaLAPACK tools routine which initializes the descriptors for the local arrays.

      USE MPI_SETUP_INT
      USE LSQRR_INT
      USE UMACH_INT
      USE WRRRN_INT
      USE SCALAPACK_SUPPORT
      IMPLICIT NONE
      INCLUDE ‘mpif.h'

! Declare variables

      INTEGER        LDA, NRA, NCA, DESCA(9), DESCX(9), DESCR(9)
      INTEGER       INFO, KBASIS, MXCOL, MXLDA, MXCOLX, MXLDX, NOUT
      REAL          TOL
      REAL, ALLOCATABLE ::        A(:,:), B(:), X(:), RES(:)
      REAL, ALLOCATABLE ::        A0(:,:), B0(:), X0(:), RES0(:)

PARAMETER (NRA=4, NCA=3, LDA=NRA)

! Set up for MPI

      MP_NPROCS = MP_SETUP()
      IF(MP_RANK .EQ. 0) THEN
          ALLOCATE (A(LDA,NCA), B(NRA), X(NCA), RES(NRA))

! Set values for A and B

          A(1,:) = (/ 1.0, 2.0,   4.0/)
          A(2,:) = (/ 1.0, 4.0, 16.0/)
          A(3,:) = (/ 1.0, 6.0, 36.0/)
          A(4,:) = (/ 1.0, 8.0, 64.0/)
!

B = (/4.999, 9.001, 12.999, 17.001/)
ENDIF

! Set up a 2D processor grid and define

! its context ID, MP_ICTXT

CALL SCALAPACK_SETUP(NRA, NCA, .TRUE., .FALSE.)

! Get the array descriptor entities MXLDA,

! MXCOL, MXLDX, and MXCOLX

CALL SCALAPACK_GETDIM(NRA, NCA, MP_MB, MP_NB, MXLDA, MXCOL)

CALL SCALAPACK_GETDIM(NCA, 1, MP_NB, 1, MXLDX, MXCOLX)

! Set up the array descriptors

      CALL DESCINIT(DESCA, NRA, NCA, MP_MB, MP_NB, 0, 0, MP_ICTXT, MXLDA, &
                    INFO)
      CALL DESCINIT(DESCX, NCA, 1, MP_NB, 1, 0, 0, MP_ICTXT, MXLDX, INFO)
      CALL DESCINIT(DESCR, NRA, 1, MP_MB, 1, 0, 0, MP_ICTXT, MXLDA, INFO)

! Allocate space for the local arrays

ALLOCATE (A0(MXLDA,MXCOL), B0(MXLDA), X0(MXLDX), RES0(MXLDA))

! Map input arrays to the processor grid

CALL SCALAPACK_MAP(A, DESCA, A0)
CALL SCALAPACK_MAP(B, DESCR, B0)

! Solve the least squares problem
TOL = 1.0E-4

CALL LSQRR (A0, B0, X0, RES0, KBASIS, TOL=TOL)

! Unmap the results from the distributed

! arrays back to a non-distributed array.

! After the unmap, only Rank=0 has the full

! array.

CALL SCALAPACK_UNMAP(X0, DESCX, X)
CALL SCALAPACK_UNMAP(RES0, DESCR, RES)

! Print results.

! Only Rank=0 has the solution.

IF(MP_RANK .EQ. 0)THEN

CALL UMACH (2, NOUT)

WRITE (NOUT,*) ‘KBASIS = ‘, KBASIS

CALL WRRRN ('X', X, 1, NCA, 1)

CALL WRRRN ('RES', RES, 1, NRA, 1)

ENDIF

IF (MP_RANK .EQ. 0) DEALLOCATE(A, B, RES, X)

DEALLOCATE(A0, B0, RES0, X0)

! Exit ScaLAPACK usage

CALL SCALAPACK_EXIT(MP_ICTXT)

! Shut down MPI

MP_NPROCS = MP_SETUP(‘FINAL')
END