IMSL MATH/LIBRARY

Appendix A: GAMS Index

IMSL MATH/LIBRARY

A....... ARITHMETIC, ERROR ANALYSIS

A3..... Real

A3c.... Extended precision

DQADD Adds a double-precision scalar to the accumulator in extended precision.

DQINI Initializes an extended-precision accumulator with a double-precision scalar.

DQMUL Multiplies double-precision scalars in extended precision.

DQSTO Stores a double-precision approximation to an extended-precision scalar.

A4..... Complex

A4c.... Extended precision

ZQADD Adds a double complex scalar to the accumulator in extended precision.

ZQINI Initializes an extended-precision complex accumulator to a double complex scalar.

ZQMUL Multiplies double complex scalars using extended precision.

ZQSTO Stores a double complex approximation to an extended-precision complex scalar.

A6..... Change of representation

A6c.... Decomposition, construction

PRIME Decomposes an integer into its prime factors.

B....... NUMBER THEORY

PRIME Decomposes an integer into its prime factors.

C....... ELEMENTARY AND SPECIAL FUNCTIONS

C2..... Powers, roots, reciprocals

HYPOT Computes 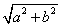without underflow or overflow.

C19.... Other special functions

CONST Returns the value of various mathematical and physical constants.

CUNIT Converts X in units XUNITS to Y in units YUNITS.

D....... LINEAR ALGEBRA

D1..... Elementary vector and matrix operations

D1a.... Elementary vector operations

D1a1.. Set to constant

CSET Sets the components of a vector to a scalar, all complex.

ISET Sets the components of a vector to a scalar, all integer.

SSET Sets the components of a vector to a scalar, all single precision.

D1a2.. Minimum and maximum components

ICAMAX Finds the smallest index of the component of a complex vector having maximum magnitude.

ICAMIN Finds the smallest index of the component of a complex vector having minimum magnitude.

IIMAX Finds the smallest index of the maximum component of a integer vector.

IIMIN Finds the smallest index of the minimum of an integer vector.

ISAMAX Finds the smallest index of the component of a single-precision vector having maximum absolute value.

ISAMIN Finds the smallest index of the component of a single-precision vector having minimum absolute value.

ISMAX Finds the smallest index of the component of a single-precision vector having maximum value.

ISMIN Finds the smallest index of the component of a single-precision vector having minimum value.

D1a3.. Norm

D1a3a L1 (sum of magnitudes)

DISL1 Computes the 1-norm distance between two points.

SASUM Sums the absolute values of the components of a single-precision vector.

SCASUM Sums the absolute values of the real part together with the absolute values of the imaginary part of the components of a complex vector.

D1a3b… L2 (Euclidean norm)

DISL2 Computes the Euclidean (2-norm) distance between two points.

NORM2,CNORM2 Computes the Euclidean length of a vector or matrix,
avoiding out-of-scale intermediate subexpressions.

MNORM2,CMNORM2 Computes the Euclidean length of a vector or matrix,
avoiding out-of-scale intermediate subexpressions

NRM2, CNRM2 Computes the Euclidean length of a vector or matrix,
avoiding out-of-scale intermediate subexpressions.

SCNRM2 Computes the Euclidean norm of a complex vector.

SNRM2 Computes the Euclidean length or L2 norm of a single-precision vector.

D1a3c L∞ (maximum magnitude)

DISLI Computes the infinity norm distance between two points.

ICAMAX Finds the smallest index of the component of a complex vector having maximum magnitude.

ISAMAX Finds the smallest index of the component of a single-precision vector having maximum absolute value.

D1a4.. Dot product (inner product)

CDOTC Computes the complex conjugate dot product, .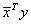

CDOTU Computes the complex dot product xTy.

CZCDOT Computes the sum of a complex scalar plus a complex conjugate dot product, 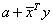, using a double-precision accumulator.

CZDOTA Computes the sum of a complex scalar, a complex dot product and the double-complex accumulator, which is set to the result ACC ¬ ACC + a + xTy.

CZDOTC Computes the complex conjugate dot product, 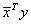, using a double-precision accumulator.

CZDOTI Computes the sum of a complex scalar plus a complex dot product using a double-complex accumulator, which is set to the result ACC ¬ a + xTy.

CZDOTU Computes the complex dot product xTy using a double-precision accumulator.

CZUDOT Computes the sum of a complex scalar plus a complex dot product, a + xTy, using a double-precision accumulator.

DSDOT Computes the single-precision dot product xTy using a double precision accumulator.

SDDOTA Computes the sum of a single-precision scalar, a single-precision dot product and the double-precision accumulator, which is set to the result
ACC ¬ ACC + a + xTy.

SDDOTI Computes the sum of a single-precision scalar plus a singleprecision dot product using a double-precision accumulator, which is set to the result ACC ¬ a + xTy.

SDOT Computes the single-precision dot product xTy.

SDSDOT Computes the sum of a single-precision scalar and a single precision dot product, a + xTy, using a double-precision accumulator.

D1a5.. Copy or exchange (swap)

CCOPY Copies a vector x to a vector y, both complex.

CSWAP Interchanges vectors x and y, both complex.

ICOPY Copies a vector x to a vector y, both integer.

ISWAP Interchanges vectors x and y, both integer.

SCOPY Copies a vector x to a vector y, both single precision.

SSWAP Interchanges vectors x and y, both single precision.

D1a6.. Multiplication by scalar

CSCAL Multiplies a vector by a scalar, y ¬ ay, both complex.

CSSCAL Multiplies a complex vector by a single-precision scalar,
y ¬ ay.

CSVCAL Multiplies a complex vector by a single-precision scalar and store the result in another complex vector, y ¬ ax.

CVCAL Multiplies a vector by a scalar and store the result in another vector, y ¬ ax, all complex.

SSCAL Multiplies a vector by a scalar, y ¬ ay, both single precision.

SVCAL Multiplies a vector by a scalar and store the result in another vector, y ¬ ax, all single precision.

D1a7.. Triad (ax + y for vectors x, y and scalar a)

CAXPY Computes the scalar times a vector plus a vector,
y ¬ ax + y, all complex.

SAXPY Computes the scalar times a vector plus a vector,
y ¬ ax + y, all single precision.

D1a8.. Elementary rotation (Givens transformation) (search also class D1b10)

CSROT Applies a complex Givens plane rotation.

CSROTM Applies a complex modified Givens plane rotation.

SROT Applies a Givens plane rotation in single precision.

SROTM Applies a modified Givens plane rotation in single precision.

D1a10 Convolutions

RCONV Computes the convolution of two real vectors.

VCONC Computes the convolution of two complex vectors.

VCONR Computes the convolution of two real vectors.

D1a11 Other vector operations

CADD Adds a scalar to each component of a vector, x ¬ x + a, all complex.

CSUB Subtracts each component of a vector from a scalar,
x ¬ a - x, all complex.

DISL1 Computes the 1-norm distance between two points.

DISL2 Computes the Euclidean (2-norm) distance between two points.

DISLI Computes the infinity norm distance between two points.

IADD Adds a scalar to each component of a vector, x ¬ x + a, all integer.

ISUB Subtracts each component of a vector from a scalar,
x ¬ a - x, all integer.

ISUM Sums the values of an integer vector.

SADD Adds a scalar to each component of a vector, x ¬ x + a, all single precision.

SHPROD Computes the Hadamard product of two single-precision vectors.

SPRDCT Multiplies the components of a single-precision vector.

SSUB Subtracts each component of a vector from a scalar,
x ¬ a - x, all single precision.

SSUM Sums the values of a single-precision vector.

SXYZ Computes a single-precision xyz product.

D1b.... Elementary matrix operations

CGERC Computes the rank-one update of a complex general matrix: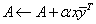
.

CGERU Computes the rank-one update of a complex general matrix:
.

CHER Computes the rank-one update of an Hermitian matrix: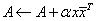
with x complex and a real.

CHER2 Computes a rank-two update of an Hermitian matrix: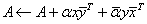
.

CHER2K Computes one of the Hermitian rank 2k operations:
,
where C is an n by n Hermitian matrix and A and B are n by k matrices in the first case and k by n matrices in the second case.

CHERK Computes one of the Hermitian rank k operations:
,
where C is an n by n Hermitian matrix and A is an n by k matrix in the first case and a k by n matrix in the second case.

CSYR2K Computes one of the symmetric rank 2k operations: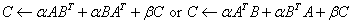
,
where C is an n by n symmetric matrix and A and B are n by k matrices in the first case and k by n matrices in the second case.

CSYRK Computes one of the symmetric rank k operations: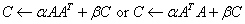
,
where C is an n by n symmetric matrix and A is an n by k matrix in the first case and a k by n matrix in the second case.

CTBSV Solves one of the complex triangular systems: ,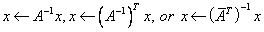
where A is a triangular matrix in band storage mode.

CTRSM Solves one of the complex matrix equations: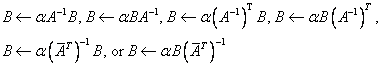
where A is a triangular matrix.

CTRSV Solves one of the complex triangular systems:
,
where A is a triangular matrix.

HRRRR Computes the Hadamard product of two real rectangular matrices.

SGER Computes the rank-one update of a real general matrix:
.

SSYR Computes the rank-one update of a real symmetric matrix: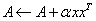
.

SSYR2 Computes the rank-two update of a real symmetric matrix: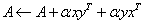
.

SSYR2K Computes one of the symmetric rank 2k operations: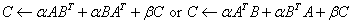
,
where C is an n by n symmetric matrix and A and B are n by k matrices in the first case and k by n matrices in the second case.

SSYRK Computes one of the symmetric rank k operations: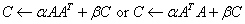
,
where C is an n by n symmetric matrix and A is an n by k matrix in the first case and a k by n matrix in the second case.

STBSV Solves one of the triangular systems: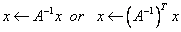
,
where A is a triangular matrix in band storage mode.

STRSM Solves one of the matrix equations: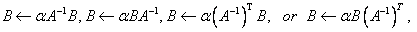
where B is an m by n matrix and A is a triangular matrix.

STRSV Solves one of the triangular linear systems: ,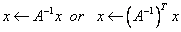

where A is a triangular matrix.

D1b2.. Norm

NR1CB Computes the 1-norm of a complex band matrix in band storage mode.

NR1RB Computes the 1-norm of a real band matrix in band storage mode.

NR1RR Computes the 1-norm of a real matrix.

NR2RR Computes the Frobenius norm of a real rectangular matrix.

NRIRR Computes the infinity norm of a real matrix.

D1b3.. Transpose

TRNRR Transposes a rectangular matrix.

D1b4 Multiplication by vector

BLINF Computes the bilinear form xTAy.

CGBMV Computes one of the matrix-vector operations: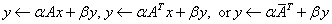
,
where A is a matrix stored in band storage mode.

CGEMV Computes one of the matrix-vector operations: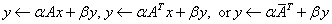
,

CHBMV Computes the matrix-vector operation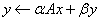
,
where A is an Hermitian band matrix in band Hermitian storage.

CHEMV Computes the matrix-vector operation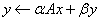
,
where A is an Hermitian matrix.

CTBMV Computes one of the matrix-vector operations: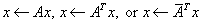
,
where A is a triangular matrix in band storage mode.

CTRMV Computes one of the matrix-vector operations: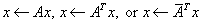
,
where A is a triangular matrix.

MUCBV Multiplies a complex band matrix in band storage mode by a complex vector.

MUCRV Multiplies a complex rectangular matrix by a complex vector.

MURBV Multiplies a real band matrix in band storage mode by a real vector.

MURRV Multiplies a real rectangular matrix by a vector.

SGBMV Computes one of the matrix-vector operations: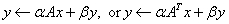
,
where A is a matrix stored in band storage mode.

SGEMV Computes one of the matrix-vector operations: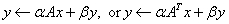
,

SSBMV Computes the matrix-vector operation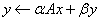
,
where A is a symmetric matrix in band symmetric storage mode.

SSYMV Computes the matrix-vector operation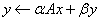
,
where A is a symmetric matrix.

STBMV Computes one of the matrix-vector operations: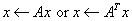
,
where A is a triangular matrix in band storage mode.

STRMV Computes one of the matrix-vector operations: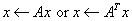
,
where A is a triangular matrix.

D1b5.. Addition, subtraction

ACBCB Adds two complex band matrices, both in band storage mode.

ARBRB Adds two band matrices, both in band storage mode.

D1b6.. Multiplication

CGEMM Computes one of the matrix-matrix operations:

CHEMM Computes one of the matrix-matrix operations: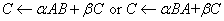
,
where A is an Hermitian matrix and B and C are m by n matrices.

CSYMM Computes one of the matrix-matrix operations: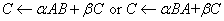
,
where A is a symmetric matrix and B and C are m by n matrices.

CTRMM Computes one of the matrix-matrix operations:

where B is an m by n matrix and A is a triangular matrix.

MCRCR Multiplies two complex rectangular matrices, AB.

MRRRR Multiplies two real rectangular matrices, AB.

MXTXF Computes the transpose product of a matrix, ATA.

MXTYF Multiplies the transpose of matrix A by matrix B, ATB.

MXYTF Multiplies a matrix A by the transpose of a matrix B, ABT.

SGEMM Compute one of the matrix-matrix operations: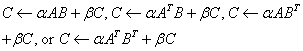
.

SSYMM Computes one of the matrix-matrix operations: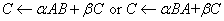
,
where A is a symmetric matrix and B and C are m by n matrices.

STRMM Computes one of the matrix-matrix operations: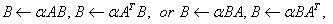

where B is an m by n matrix and A is a triangular matrix.

D1b7.. Matrix polynomial

POLRG 1207 Evaluates a real general matrix polynomial.

D1b8.. Copy

CCBCB Copies a complex band matrix stored in complex band storage mode.

CCGCG Copies a complex general matrix.

CRBRB Copies a real band matrix stored in band storage mode.

CRGRG Copies a real general matrix.

D1b9.. Storage mode conversion

CCBCG Converts a complex matrix in band storage mode to a complex matrix in full storage mode.

CCGCB Converts a complex general matrix to a matrix in complex band storage mode.

CHBCB Copies a complex Hermitian band matrix stored in band Hermitian storage mode to a complex band matrix stored in band storage mode.

CHFCG Extends a complex Hermitian matrix defined in its upper triangle to its lower triangle.

CRBCB Converts a real matrix in band storage mode to a complex matrix in band storage mode.

CRBRG Converts a real matrix in band storage mode to a real general matrix.

CRGCG Copies a real general matrix to a complex general matrix.

CRGRB Converts a real general matrix to a matrix in band storage mode.

CRRCR Copies a real rectangular matrix to a complex rectangular matrix.

CSBRB Copies a real symmetric band matrix stored in band symmetric storage mode to a real band matrix stored in band storage mode.

CSFRG Extends a real symmetric matrix defined in its upper triangle to its lower triangle.

D1b10 Elementary rotation (Givens transformation) (search also class D1a8)

SROTG Constructs a Givens plane rotation in single precision.

SROTMG Constructs a modified Givens plane rotation in single precision.

D2..... Solution of systems of linear equations (including inversion, LU and related decompositions)

D2a.... Real nonsymmetric matrices

LSLTO Solves a real Toeplitz linear system.

D2a1.. General

LFCRG Computes the LU factorization of a real general matrix and estimate its L1 condition number.

LFIRG Uses iterative refinement to improve the solution of a real general system of linear equations.

LFSRG Solves a real general system of linear equations given the LU factorization of the coefficient matrix.

LFTRG Computes the LU factorization of a real general matrix.

LINRG Computes the inverse of a real general matrix.

LSARG Solves a real general system of linear equations with iterative refinement.

LSLRG Solves a real general system of linear equations without iterative refinement.

LIN_SOL_GEN Solves a general system of linear equations Ax = b. Using optional arguments, any of several related computations can be performed. These extra tasks include computing the LU factorization of A using partial pivoting, representing the determinant of A, computing the inverse matrix A-1, and solving ATx = b or Ax = b given the LU factorization of A.

D2a2.. Banded

LFCRB Computes the LU factorization of a real matrix in band storage mode and estimate its L1 condition number.

LFIRB Uses iterative refinement to improve the solution of a real system of linear equations in band storage mode.

LFSRB Solves a real system of linear equations given the LU factorization of the coefficient matrix in band storage mode.

LFTRB Computes the LU factorization of a real matrix in band storage mode.

LSARB Solves a real system of linear equations in band storage mode with iterative refinement.

LSLRB Solves a real system of linear equations in band storage mode without iterative refinement.

STBSV Solves one of the triangular systems: ,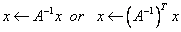
where A is a triangular matrix in band storage mode.

D2a2a Tridiagonal

LSLCR Computes the LDU factorization of a real tridiagonal matrix A using a cyclic reduction algorithm.

LSLTR Solves a real tridiagonal system of linear equations.

LIN_SOL_TRI Solves multiple systems of linear equations Ajxj = yj, j = 1, ¼, k. Each matrix Aj is tridiagonal with the same dimension, n: The default solution method is based on LU factorization computed using cyclic reduction. An option is used to select Gaussian elimination with partial pivoting.

TRI_SOLVE A real, tri-diagonal, multiple system solver. Uses both cyclic reduction and Gauss elimination. Similar in function to lin_sol_tri.

D2a3.. Triangular

LFCRT Estimates the condition number of a real triangular matrix.

LINRT Computes the inverse of a real triangular matrix.

LSLRT Solves a real triangular system of linear equations.

STRSM Solves one of the matrix equations:

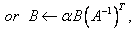
where B is an m by n matrix and A is a triangular matrix.

STRSV Solves one of the triangular linear systems: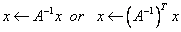

where A is a triangular matrix.

D2a4.. Sparse

LFSXG Solves a sparse system of linear equations given the LU factorization of the coefficient matrix.

LFTXG Computes the LU factorization of a real general sparse matrix.

LSLXG Solves a sparse system of linear algebraic equations by Gaussian elimination.

GMRES Uses restarted GMRES with reverse communication to generate an approximate solution of Ax = b.

D2b.... Real symmetric matrices

D2b1.. General

D2b1a. Indefinite

LCHRG Computes the Cholesky decomposition of a symmetric positive semidefinite matrix with optional column pivoting.

LFCSF Computes the U DUT factorization of a real symmetric matrix and estimate its L1 condition number.

LFISF Uses iterative refinement to improve the solution of a real symmetric system of linear equations.

LFSSF Solves a real symmetric system of linear equations given the U DUT factorization of the coefficient matrix.

LFTSF Computes the U DUT factorization of a real symmetric matrix.

LSASF Solves a real symmetric system of linear equations with iterative refinement.

LSLSF Solves a real symmetric system of linear equations without iterative refinement.

LIN_SOL_SELF Solves a system of linear equations Ax = b, where A is a self-adjoint matrix. Using optional arguments, any of several related computations can be performed. These extra tasks include computing and saving the factorization of A using symmetric pivoting, representing the determinant of A, computing the inverse matrix A-1, or computing the solution of Ax = b given the factorization of A. An optional argument is provided indicating that A is positive definite so that the Cholesky decomposition can be used.

D2b1b. Positive definite

LCHRG Computes the Cholesky decomposition of a symmetric positive semidefinite matrix with optional column pivoting.

LFCDS Computes the RT R Cholesky factorization of a real symmetric positive definite matrix and estimate its L1condition number.

LFIDS Uses iterative refinement to improve the solution of a real symmetric positive definite system of linear equations.

LFSDS Solves a real symmetric positive definite system of linear equations given the RT R Choleksy factorization of the coefficient matrix.

LFTDS Computes the RT R Cholesky factorization of a real symmetric positive definite matrix.

LINDS Computes the inverse of a real symmetric positive definite matrix.

LSADS Solves a real symmetric positive definite system of linear equations with iterative refinement.

LSLDS Solves a real symmetric positive definite system of linear equations without iterative refinement.

D2b2.. Positive definite banded

LFCQS Computes the RT R Cholesky factorization of a real symmetric positive definite matrix in band symmetric storage mode and estimate its L1 condition number.

LFDQS Computes the determinant of a real symmetric positive definite matrix given the RT R Cholesky factorization of the band symmetric storage mode.

LFIQS Uses iterative refinement to improve the solution of a real symmetric positive definite system of linear equations in band symmetric storage mode.

LFSQS Solves a real symmetric positive definite system of linear equations given the factorization of the coefficient matrix in band symmetric storage mode.

LFTQS Computes the RT R Cholesky factorization of a real symmetric positive definite matrix in band symmetric storage mode.

LSAQS Solves a real symmetric positive definite system of linear equations in band symmetric storage mode with iterative refinement.

LSLPB Computes the RT DR Cholesky factorization of a real symmetric positive definite matrix A in codiagonal band symmetric storage mode. Solve a system Ax = b.

LSLQS Solves a real symmetric positive definite system of linear equations in band symmetric storage mode without iterative refinement.

D2b4.. Sparse

JCGRC Solves a real symmetric definite linear system using the Jacobi preconditioned conjugate gradient method with reverse communication.

LFSXD Solves a real sparse symmetric positive definite system of linear equations, given the Cholesky factorization of the coefficient matrix.

LNFXD Computes the numerical Cholesky factorization of a sparse symmetrical matrix A.

LSCXD Performs the symbolic Cholesky factorization for a sparse symmetric matrix using a minimum degree ordering or a userspecified ordering, and set up the data structure for the numerical Cholesky factorization.

LSLXD Solves a sparse system of symmetric positive definite linear algebraic equations by Gaussian elimination.

PCGRC Solves a real symmetric definite linear system using a preconditioned conjugate gradient method with reverse communication.

D2c.... Complex non-Hermitian matrices

LSLCC Solves a complex circulant linear system.

LSLTC Solves a complex Toeplitz linear system.

D2c1.. General

LFCCG Computes the LU factorization of a complex general matrix and estimate its L1 condition number.

LFICG Uses iterative refinement to improve the solution of a complex general system of linear equations.

LFSCG Solves a complex general system of linear equations given the LU factorization of the coefficient matrix.

LFTCG Computes the LU factorization of a complex general matrix.

LINCG Computes the inverse of a complex general matrix.

LSACG Solves a complex general system of linear equations with iterative refinement.

LSLCG Solves a complex general system of linear equations without iterative refinement.

D2c2.. Banded

CTBSV Solves one of the complex triangular systems: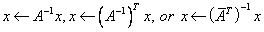
,
where A is a triangular matrix in band storage mode.

LFCCB Computes the LU factorization of a complex matrix in band storage mode and estimate its L1condition number.

LFICB Uses iterative refinement to improve the solution of a complex system of linear equations in band storage mode.

LFSCB Solves a complex system of linear equations given the LU factorization of the coefficient matrix in band storage mode.

LFTCB Computes the LU factorization of a complex matrix in band storage mode.

LSACB Solves a complex system of linear equations in band storage mode with iterative refinement.

LSLCB Solves a complex system of linear equations in band storage mode without iterative refinement.

D2c2a Tridiagonal

LSLCQ Computes the LDU factorization of a complex tridiagonal matrix A using a cyclic reduction algorithm.

LSLTQ Solves a complex tridiagonal system of linear equations.

D2c3.. Triangular

CTRSM Solves one of the complex matrix equations: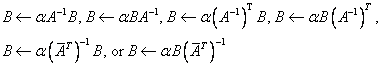
where A is a traiangular matrix.

CTRSV Solves one of the complex triangular systems:

where A is a triangular matrix.

LFCCT Estimates the condition number of a complex triangular matrix.

LINCT Computes the inverse of a complex triangular matrix.

LSLCT Solves a complex triangular system of linear equations.

D2c4.. Sparse

LFSZG Solves a complex sparse system of linear equations given the LU factorization of the coefficient matrix.

LFTZG Computes the LU factorization of a complex general sparse matrix.

LSLZG Solves a complex sparse system of linear equations by Gaussian elimination.

D2d.... Complex Hermitian matrices

D2d1.. General

D2d1a. Indefinite

LFCHF Computes the U DUH factorization of a complex Hermitian matrix and estimate its L1 condition number.

LFDHF Computes the determinant of a complex Hermitian matrix given the U DUH factorization of the matrix.

LFIHF Uses iterative refinement to improve the solution of a complex Hermitian system of linear equations.

LFSHF Solves a complex Hermitian system of linear equations given the U DUH factorization of the coefficient matrix.

LFTHF Computes the U DUH factorization of a complex Hermitian matrix.

LSAHF Solves a complex Hermitian system of linear equations with iterative refinement.

LSLHF Solves a complex Hermitian system of linear equations without iterative refinement.

D2d1b. Positive definite

LFCDH Computes the RH R factorization of a complex Hermitian positive definite matrix and estimate its L1 condition number.

LFIDH Uses iterative refinement to improve the solution of a complex Hermitian positive definite system of linear equations.

LFSDH Solves a complex Hermitian positive definite system of linear equations given the RH R factorization of the coefficient matrix.

LFTDH Computes the RH R factorization of a complex Hermitian positive definite matrix.

LSADH Solves a Hermitian positive definite system of linear equations with iterative refinement.

LSLDH Solves a complex Hermitian positive definite system of linear equations without iterative refinement.

D2d2.. Positive definite banded

LFCQH Computes the RH R factorization of a complex Hermitian positive definite matrix in band Hermitian storage mode and estimate its L1 condition number.

LFIQH Uses iterative refinement to improve the solution of a complex Hermitian positive definite system of linear equations in band Hermitian storage mode.

LFSQH Solves a complex Hermitian positive definite system of linear equations given the factorization of the coefficient matrix in band Hermitian storage mode.

LFTQH Computes the RH R factorization of a complex Hermitian positive definite matrix in band Hermitian storage mode.

LSAQH Solves a complex Hermitian positive definite system of linear equations in band Hermitian storage mode with iterative refinement.

LSLQB Computes the RH DR Cholesky factorization of a complex hermitian positive-definite matrix A in codiagonal band hermitian storage mode. Solve a system Ax = b.

LSLQH Solves a complex Hermitian positive definite system of linearequations in band Hermitian storage mode without iterative refinement.

D2d4.. Sparse

LFSZD Solves a complex sparse Hermitian positive definite system of linear equations, given the Cholesky factorization of the coefficient matrix.

LNFZD Computes the numerical Cholesky factorization of a sparse Hermitian matrix A.

LSLZD Solves a complex sparse Hermitian positive definite system of linear equations by Gaussian elimination.

D3..... Determinants

D3a.... Real nonsymmetric matrices

D3a1.. General

LFDRG Computes the determinant of a real general matrix given the LU factorization of the matrix.

D3a2.. Banded

LFDRB Computes the determinant of a real matrix in band storage mode given the LU factorization of the matrix.

D3a3.. Triangular

LFDRT Computes the determinant of a real triangular matrix.

D3b.... Real symmetric matrices

D3b1.. General

D3b1a. Indefinite

LFDSF Computes the determinant of a real symmetric matrix given the U DUT factorization of the matrix.

D3b1b. Positive definite

LFDDS Computes the determinant of a real symmetric positive definite matrix given the RH R Cholesky factorization of the matrix.

D3c.... Complex non-Hermitian matrices

D3c1.. General

LFDCG Computes the determinant of a complex general matrix given the LU factorization of the matrix.

D3c2.. Banded

LFDCB Computes the determinant of a complex matrix given the LU factorization of the matrix in band storage mode.

D3c3.. Triangular

LFDCT Computes the determinant of a complex triangular matrix.

D3d.... Complex Hermitian matrices

D3d1.. General

D3d1b. Positive definite

LFDDH Computes the determinant of a complex Hermitian positive definite matrix given the RH R Cholesky factorization of the matrix.

D3d2.. Positive definite banded

LFDQH Computes the determinant of a complex Hermitian positive definite matrix given the RH R Cholesky factorization in band Hermitian storage mode.

D4..... Eigenvalues, eigenvectors

D4a.... Ordinary eigenvalue problems (Ax = lx)

D4a1.. Real symmetric

EVASF Computes the largest or smallest eigenvalues of a real symmetric matrix.

EVBSF Computes selected eigenvalues of a real symmetric matrix.

EVCSF Computes all of the eigenvalues and eigenvectors of a real symmetric matrix.

EVESF Computes the largest or smallest eigenvalues and the corresponding eigenvectors of a real symmetric matrix.

EVFSF Computes selected eigenvalues and eigenvectors of a real symmetric matrix.

EVLSF Computes all of the eigenvalues of a real symmetric matrix.

LIN_EIG_SELF Computes the eigenvalues of a self-adjoint matrix, A. Optionally, the eigenvectors can be computed. This gives the decomposition A = VDVT, where V is an n ´ n orthogonal matrix and D is a real diagonal matrix.

D4a2.. Real nonsymmetric

EVCRG Computes all of the eigenvalues and eigenvectors of a real matrix.

EVLRG Computes all of the eigenvalues of a real matrix.

LIN_EIG_GEN Computes the eigenvalues of an n ´ n matrix, A. Optionally, the eigenvectors of A or AT are computed. Using the eigenvectors of A gives the decomposition
AV = VE, where V is an n ´ n complex matrix of eigenvectors, and E is the complex diagonal matrix of eigenvalues. Other options include the reduction of A to upper triangular or Schur form, reduction to block upper triangular form with 2 ´ 2 or unit sized diagonal block matrices, and reduction to upper Hessenberg form.

D4a3.. Complex Hermitian

EVAHF Computes the largest or smallest eigenvalues of a complex Hermitian matrix.

EVBHF Computes the eigenvalues in a given range of a complex Hermitian matrix.

EVCHF Computes all of the eigenvalues and eigenvectors of a complex Hermitian matrix.

EVEHF Computes the largest or smallest eigenvalues and the corresponding eigenvectors of a complex Hermitian matrix.

EVFHF Computes the eigenvalues in a given range and the corresponding eigenvectors of a complex Hermitian matrix.

EVLHF Computes all of the eigenvalues of a complex Hermitian matrix.

D4a4.. Complex non-Hermitian

EVCCG Computes all of the eigenvalues and eigenvectors of a complex matrix.

EVLCG Computes all of the eigenvalues of a complex matrix.

D4a6.. Banded

EVASB Computes the largest or smallest eigenvalues of a real symmetric matrix in band symmetric storage mode.

EVBSB Computes the eigenvalues in a given interval of a real symmetric matrix stored in band symmetric storage mode.

EVCSB Computes all of the eigenvalues and eigenvectors of a real symmetric matrix in band symmetric storage mode.

EVESB Computes the largest or smallest eigenvalues and the corresponding eigenvectors of a real symmetric matrix in band symmetric storage mode.

EVFSB Computes the eigenvalues in a given interval and the corresponding eigenvectors of a real symmetric matrix stored in band symmetric storage mode.

EVLSB Computes all of the eigenvalues of a real symmetric matrix in band symmetric storage mode.

D4b.... Generalized eigenvalue problems (e.g., Ax = lBx)

D4b1.. Real symmetric

GVCSP Computes all of the eigenvalues and eigenvectors of the generalized real symmetric eigenvalue problem Az = lBz, with B symmetric positive definite.

GVLSP Computes all of the eigenvalues of the generalized real symmetric eigenvalue problem Az = lBz, with B symmetric positive definite.

LIN_GEIG_GEN Computes the generalized eigenvalues of an n ´ n matrix pencil, Av @ lBv. Optionally, the generalized eigenvectors are computed. If either of A or B is nonsingular, there are diagonal matrices a and b and a complex matrix V computed such that AVb = BVa.

D4b2.. Real general

GVCRG Computes all of the eigenvalues and eigenvectors of a generalized real eigensystem Az = lBz.

GVLRG Computes all of the eigenvalues of a generalized real eigensystem Az = lBz.

D4b4.. Complex general

GVCCG Computes all of the eigenvalues and eigenvectors of a generalized complex eigensystem Az = lBz.

GVLCG Computes all of the eigenvalues of a generalized complex eigensystem Az = lBz.

D4c.... Associated operations

BALANC, CBSLANC Balances a general matrix before computing the eigenvalue-eigenvector decomposition.

EPICG Computes the performance index for a complex eigensystem.

EPIHF Computes the performance index for a complex Hermitian eigensystem.

EPIRG Computes the performance index for a real eigensystem.

EPISB Computes the performance index for a real symmetric eigensystem in band symmetric storage mode.

EPISF Computes the performance index for a real symmetric eigensystem.

GPICG Computes the performance index for a generalized complex eigensystem Az = lBz.

GPIRG Computes the performance index for a generalized real eigensystem Az = lBz.

GPISP Computes the performance index for a generalized real symmetric eigensystem problem.

PERFECT_SHIFT Computes eigenvectors using actual eigenvalue as an explicit shift. Called by lin_eig_self.

PWK A rational QR algorithm for computing eigenvalues of real, symmetric tri-diagonal matrices. Called by lin_svd and lin_eig_self.

D4c2.. Compute eigenvalues of matrix in compact form

D4c2b. Hessenberg

EVCCH Computes all of the eigenvalues and eigenvectors of a complex upper Hessenberg matrix.

EVCRH Computes all of the eigenvalues and eigenvectors of a real upper Hessenberg matrix.

EVLCH Computes all of the eigenvalues of a complex upper Hessenberg matrix.

EVLRH Computes all of the eigenvalues of a real upper Hessenberg matrix.

D5..... QR decomposition, Gram-Schmidt orthogonalization

LQERR Accumulates the orthogonal matrix Q from its factored form given the QR factorization of a rectangular matrix A.

LQRRR Computes the QR decomposition, AP = QR, using Householder transformations.

LQRSL Computes the coordinate transformation, projection, and complete the solution of the least-squares problem Ax = b.

LSBRR Solves a linear least-squares problem with iterative refinement.

LSQRR Solves a linear least-squares problem without iterative refinement.

D6..... Singular value decomposition

LSVCR Computes the singular value decomposition of a complex matrix.

LSVRR Computes the singular value decomposition of a real matrix.

LIN_SOL_SVD Solves a rectangular least-squares system of linear equations Ax @ b using singular value decomposition,
A = USVT. Using optional arguments, any of several related computations can be performed. These extra tasks include computing the rank of A, the orthogonal m ´ m and n ´ n matrices U and V, and the m ´ n diagonal matrix of singular values, S.

LIN_SVD Computes the singular value decomposition (SVD) of a rectangular matrix, A. This gives the decomposition
A = USVT, where V is an n ´ n orthogonal matrix, U is an m ´ m orthogonal matrix, and S is a real, rectangular diagonal matrix.

D7..... Update matrix decompositions

D7b.... Cholesky

LDNCH Downdates the RTR Cholesky factorization of a real symmetric positive definite matrix after a rank-one matrix is removed.

LUPCH Updates the RTR Cholesky factorization of a real symmetric positive definite matrix after a rank-one matrix is added.

D7c.... QR

LUPQR Computes an updated QR factorization after the rank-one matrix axyT is added.

D9..... Singular, overdetermined or underdetermined systems of linear equations, generalized inverses

D9a.... Unconstrained

D9a1.. Least squares (L2) solution

BAND_
ACCUMALATION Accumulatez and solves banded least-squares problem using Householder transformations.

BAND_SOLVE Accumulatez and solves banded least-squares problem using Householder transformations.

HOUSE_HOLDER Accumulates and solves banded least-squares problem using Householder transformations.

LQRRR Computes the QR decomposition, AP = QR, using Householder transformations.

LQRRV Computes the least-squares solution using Householder transformations applied in blocked form.

LQRSL Computes the coordinate transformation, projection, and complete the solution of the least-squares problem Ax = b.

LSBRR Solves a linear least-squares problem with iterative refinement.

LSQRR Solves a linear least-squares problem without iterative refinement.

LIN_SOL_LSQ Solves a rectangular system of linear equations Ax @ b, in a least-squares sense. Using optional arguments, any of several related computations can be performed. These extra tasks include computing and saving the factorization of A using column and row pivoting, representing the determinant of A, computing the generalized inverse matrix A^†, or computing the least-squares solution of
Ax @ b or ATy @ d given the factorization of A. An optional argument is provided for computing the following unscaled covariance matrix: C = (ATA)-1.

D9b.... Constrained

D9b1.. Least squares (L2) solution

LCLSQ Solves a linear least-squares problem with linear constraints.

D9c.... Generalized inverses

LSGRR Computes the generalized inverse of a real matrix.

E....... INTERPOLATION

E1..... Univariate data (curve fitting)

E1a.... Polynomial splines (piecewise polynomials)

BSINT Computes the spline interpolant, returning the B-spline coefficients.

CSAKM Computes the Akima cubic spline interpolant.

CSCON Computes a cubic spline interpolant that is consistent with the concavity of the data.

CSDEC Computes the cubic spline interpolant with specified derivative endpoint conditions.

CSHER Computes the Hermite cubic spline interpolant.

CSIEZ Computes the cubic spline interpolant with the ‘not-a-knot' condition and return values of the interpolant at specified points.

CSINT Computes the cubic spline interpolant with the ‘not-a-knot' condition.

CSPER Computes the cubic spline interpolant with periodic boundary conditions.

QDVAL Evaluates a function defined on a set of points using quadratic interpolation.

SPLEZ Computes the values of a spline that either interpolates or fits user-supplied data.

SPLINE_FITTING Solves constrained least-squares fitting of one-dimensional data by B-splines.

SPlINE_SUPPORT B-spline function and derivative evaluation package.

E2..... Multivariate data (surface fitting)

E2a.... Gridded

BS2IN Computes a two-dimensional tensor-product spline interpolant, returning the tensor-product B-spline coefficients.

BS3IN Computes a three-dimensional tensor-product spline interpolant, returning the tensor-product B-spline coefficients.

QD2DR Evaluates the derivative of a function defined on a rectangular grid using quadratic interpolation.

QD2VL Evaluates a function defined on a rectangular grid using quadratic interpolation.

QD3DR Evaluates the derivative of a function defined on a rectangular three-dimensional grid using quadratic interpolation.

QD3VL Evaluates a function defined on a rectangular three-dimensional grid using quadratic interpolation.

SURFACE_FITTING Solves constrained least-squares fitting of two-dimensional data by tensor products of B-splines.

E2b.... Scattered

SURF Computes a smooth bivariate interpolant to scattered data that is locally a quintic polynomial in two variables.

SURFACE_FAIRING Constrained weighted least-squares fitting of tensor product B-splines to discrete data, with covariance matrix and constraints at points.

E3..... Service routines for interpolation

E3a.... Evaluation of fitted functions, including quadrature

E3a1.. Function evaluation

BS1GD Evaluates the derivative of a spline on a grid, given its B-spline representation.

BS2DR Evaluates the derivative of a two-dimensional tensor-product spline, given its tensor-product B-spline representation.

BS2GD Evaluates the derivative of a two-dimensional tensor-product spline, given its tensor-product B-spline representation on a grid.

BS2VL Evaluates a two-dimensional tensor-product spline, given its tensor-product B-spline representation.

BS3GD Evaluates the derivative of a three-dimensional tensor-product spline, given its tensor-product B-spline representation on a grid.

BS3VL Evaluates a three-dimensional tensor-product spline, given its tensor-product B-spline representation.

BSVAL Evaluates a spline, given its B-spline representation.

CSVAL Evaluates a cubic spline.

PPVAL Evaluates a piecewise polynomial.

QDDER Evaluates the derivative of a function defined on a set of points using quadratic interpolation.

E3a2.. Derivative evaluation

BS1GD Evaluates the derivative of a spline on a grid, given its B-spline representation.

BS2DR Evaluates the derivative of a two-dimensional tensor-product spline, given its tensor-product B-spline representation.

BS2GD Evaluates the derivative of a two-dimensional tensor-product spline, given its tensor-product B-spline representation on a grid.

BS3DR Evaluates the derivative of a three-dimensional tensor-product spline, given its tensor-product B-spline representation.

BS3GD Evaluates the derivative of a three-dimensional tensor-product spline, given its tensor-product B-spline representation on a grid.

BSDER Evaluates the derivative of a spline, given its B-spline representation.

CS1GD Evaluates the derivative of a cubic spline on a grid.

CSDER Evaluates the derivative of a cubic spline.

PP1GD Evaluates the derivative of a piecewise polynomial on a grid.

PPDER Evaluates the derivative of a piecewise polynomial.

QDDER Evaluates the derivative of a function defined on a set of points using quadratic interpolation.

E3a3.. Quadrature

BS2IG Evaluates the integral of a tensor-product spline on a rectangular domain, given its tensor-product B-spline representation.

BS3IG Evaluates the integral of a tensor-product spline in three dimensions over a three-dimensional rectangle, given its tensorproduct B-spline representation.

BSITG Evaluates the integral of a spline, given its B-spline representation.

CSITG Evaluates the integral of a cubic spline.

E3b.... Grid or knot generation

BSNAK Computes the ‘not-a-knot' spline knot sequence.

BSOPK Computes the ‘optimal' spline knot sequence.

E3c.... Manipulation of basis functions (e.g., evaluation, change of basis)

BSCPP Converts a spline in B-spline representation to piecewise polynomial representation.

F....... SOLUTION OF NONLINEAR EQUATIONS

F1..... Single equation

F1a.... Polynomial

F1a1.. Real coefficients

ZPLRC Finds the zeros of a polynomial with real coefficients using Laguerre's method.

ZPORC Finds the zeros of a polynomial with real coefficients using the Jenkins-Traub three-stage algorithm.

F1a2.. Complex coefficients

ZPOCC Finds the zeros of a polynomial with complex coefficients using the Jenkins-Traub three-stage algorithm.

F1b.... Nonpolynomial

ZANLY Finds the zeros of a univariate complex function using Müller's method.

ZBREN Finds a zero of a real function that changes sign in a given interval.

ZREAL Finds the real zeros of a real function using Müller's method.

F2..... System of equations

NEQBF Solves a system of nonlinear equations using factored secant update with a finite-difference approximation to the Jacobian.

NEQBJ Solves a system of nonlinear equations using factored secant update with a user-supplied Jacobian.

NEQNF Solves a system of nonlinear equations using a modified Powell hybrid algorithm and a finite-difference approximation to the Jacobian.

NEQNJ Solves a system of nonlinear equations using a modified Powell hybrid algorithm with a user-supplied Jacobian.

G....... OPTIMIZATION (search also classes K, L8)

G1..... Unconstrained

G1a.... Univariate

G1a1.. Smooth function

G1a1a. User provides no derivatives

UVMIF Finds the minimum point of a smooth function of a single variable using only function evaluations.

G1a1b User provides first derivatives

UVMID Finds the minimum point of a smooth function of a single variable using both function evaluations and first derivative evaluations.

G1a2.. General function (no smoothness assumed)

UVMGS Finds the minimum point of a nonsmooth function of a single variable.

G1b.... Multivariate

G1b1.. Smooth function

G1b1a. User provides no derivatives

UMCGF Minimizes a function of N variables using a conjugate gradient algorithm and a finite-difference gradient.

UMINF Minimizes a function of N variables using a quasi-New method and a finite-difference gradient.

UNLSF Solves a nonlinear least squares problem using a modified Levenberg-Marquardt algorithm and a finite-difference Jacobian.

G1b1b. User provides first derivatives

UMCGG Minimizes a function of N variables using a conjugate gradient algorithm and a user-supplied gradient.

UMIDH Minimizes a function of N variables using a modified Newton method and a finite-difference Hessian.

UMING Minimizes a function of N variables using a quasi-New method and a user-supplied gradient.

UNLSJ Solves a nonlinear least squares problem using a modified Levenberg-Marquardt algorithm and a user-supplied Jacobian.

G1b1c. User provides first and second derivatives

UMIAH Minimizes a function of N variables using a modified Newton method and a user-supplied Hessian.

G1b2.. General function (no smoothness assumed)

UMPOL Minimizes a function of N variables using a direct search polytope algorithm.

G2..... Constrained

G2a.... Linear programming

G2a1.. Dense matrix of constraints

DLPRS Solves a linear programming problem via the revised simplex algorithm.

G2a2.. Sparse matrix of constraints

SLPRS Solves a sparse linear programming problem via the revised simplex algorithm.

G2e.... Quadratic programming

G2e1.. Positive definite Hessian (i.e., convex problem)

QPROG Solves a quadratic programming problem subject to linear equality/inequality constraints.

G2h.... General nonlinear programming

G2h1.. Simple bounds

G2h1a. Smooth function

G2h1a1 User provides no derivatives

BCLSF Solves a nonlinear least squares problem subject to bounds on the variables using a modified Levenberg-Marquardt algorithm and a finite-difference Jacobian.

BCONF Minimizes a function of N variables subject to bounds the variables using a quasi-Newton method and a finite-difference gradient.

G2h1a2 User provides first derivatives

BCLSJ Solves a nonlinear least squares problem subject to bounds on the variables using a modified Levenberg-Marquardt algorithm and a user-supplied Jacobian.

BCODH Minimizes a function of N variables subject to bounds the variables using a modified Newton method and a finite-difference Hessian.

BCONG Minimizes a function of N variables subject to bounds the variables using a quasi-Newton method and a user-supplied gradient.

G2h1a3 User provides first and second derivatives

BCOAH Minimizes a function of N variables subject to bounds the variables using a modified Newton method and a user-supplied Hessian.

G2h1b General function (no smoothness assumed)

BCPOL Minimizes a function of N variables subject to bounds the variables using a direct search complex algorithm.

G2h2.. Linear equality or inequality constraints

G2h2a. Smooth function

G2h2a1 User provides no derivatives

LCONF Minimizes a general objective function subject to linear equality/inequality constraints.

G2h2a2 User provides first derivatives

LCONG Minimizes a general objective function subject to linear equality/inequality constraints.

G2h3.. Nonlinear constraints

G2h3b Equality and inequality constraints

NNLPG Uses a sequential equality constrained QP method.

NNLPF Uses a sequential equality constrained QP method.

G2h3b1 Smooth function and constraints

G2h3b1a. User provides no derivatives

G2h3b1b User provides first derivatives of function and constraints

G4..... Service routines

G4c.... Check user-supplied derivatives

CHGRD Checks a user-supplied gradient of a function.

CHHES Checks a user-supplied Hessian of an analytic function.

CHJAC Checks a user-supplied Jacobian of a system of equations with M functions in N unknowns.

G4d.... Find feasible point

GGUES Generates points in an N-dimensional space.

G4f.... Other

CDGRD Approximates the gradient using central differences.

FDGRD Approximates the gradient using forward differences.

FDHES Approximates the Hessian using forward differences and function values.

FDJAC Approximates the Jacobian of M functions in N unknowns using forward differences.

GDHES Approximates the Hessian using forward differences and a user-supplied gradient.

H....... DIFFERENTIATION, INTEGRATION

H1..... Numerical differentiation

DERIV Computes the first, second or third derivative of a user-supplied function.

H2..... Quadrature (numerical evaluation of definite integrals)

H2a.... One-dimensional integrals

H2a1.. Finite interval (general integrand)

H2a1a Integrand available via user-defined procedure

H2a1a1. Automatic (user need only specify required accuracy)

QDAG Integrates a function using a globally adaptive scheme based on Gauss-Kronrod rules.

QDAGS Integrates a function (which may have endpoint singularities).

QDNG Integrates a smooth function using a nonadaptive rule.

H2a2.. Finite interval (specific or special type integrand including weight functions, oscillating and singular integrands, principal value integrals, splines, etc.)

H2a2a Integrand available via user-defined procedure

H2a2a1 Automatic (user need only specify required accuracy)

QDAGP Integrates a function with singularity points given.

QDAWC Integrates a function F(X)/(X - C) in the Cauchy principal value sense.

QDAWO Integrates a function containing a sine or a cosine.

QDAWS Integrates a function with algebraic-logarithmic singularities.

H2a2b Integrand available only on grid

H2a2b1 Automatic (user need only specify required accuracy)

BSITG Evaluates the integral of a spline, given its B-spline representation.

H2a3.. Semi-infinite interval (including e-x weight function)

H2a3a. Integrand available via user-defined procedure

H2a3a1. Automatic (user need only specify required accuracy)

QDAGI Integrates a function over an infinite or semi-infinite interval.

QDAWF Computes a Fourier integral.

H2b.... Multidimensional integrals

H2b1.. One or more hyper-rectangular regions (including iterated integrals)

QMC Integrates a function over a hyperrectangle using a
quasi-Monte Carlo method.

H2b1a. Integrand available via user-defined procedure

H2b1a1 Automatic (user need only specify required accuracy)

QAND Integrates a function on a hyper-rectangle.

TWODQ Computes a two-dimensional iterated integral.

H2b1b Integrand available only on grid

H2b1b2 Nonautomatic

BS2IG Evaluates the integral of a tensor-product spline on a rectangular domain, given its tensor-product B-spline representation.

BS3IG Evaluates the integral of a tensor-product spline in three dimensions over a three-dimensional rectangle, given its tensorproduct B-spline representation.

H2c.... Service routines (compute weight and nodes for quadrature formulas)

FQRUL Computes a Fejér quadrature rule with various classical weight functions.

GQRCF Computes a Gauss, Gauss-Radau or Gauss-Lobatto quadrature rule given the recurrence coefficients for the monic polynomials orthogonal with respect to the weight function.

GQRUL Computes a Gauss, Gauss-Radau, or Gauss-Lobatto quadrature rule with various classical weight functions.

RECCF Computes recurrence coefficients for various monic polynomials.

RECQR Computes recurrence coefficients for monic polynomials given a quadrature rule.

I........ DIFFERENTIAL AND INTEGRAL EQUATIONS

I1...... Ordinary differential equations (ODE's)

I1a.... Initial value problems

I1a1... General, nonstiff or mildly stiff

I1a1a. One-step methods (e.g., Runge-Kutta)

IVMRK Solves an initial-value problem y¢ = f(t, y) for ordinary differential equations using Runge-Kutta pairs of various orders.

IVPRK Solves an initial-value problem for ordinary differential equations using the Runge-Kutta-Verner fifth-order and sixth-order method.

I1a1b. Multistep methods (e.g., Adams predictor-corrector)

IVPAG Solves an initial-value problem for ordinary differential equations using either Adams-Moulton's or Gear's BDF method.

I1a2... Stiff and mixed algebraic-differential equations

DASPG Solves a first order differential-algebraic system of equations, g(t, y, y¢) = 0, using Petzold−Gear BDF method.

I1b.... Multipoint boundary value problems

I1b2... Nonlinear

BVPFD Solves a (parameterized) system of differential equations with boundary conditions at two points, using a variable order, variable step size finite-difference method with deferred corrections.

BVPMS Solves a (parameterized) system of differential equations with boundary conditions at two points, using a multiple-shooting method.

I1b3... Eigenvalue (e.g., Sturm-Liouville)

SLCNT Calculates the indices of eigenvalues of a Sturm-Liouville problem with boundary conditions (at regular points) in a specified subinterval of the real line, [a, b].

SLEIG Determines eigenvalues, eigenfunctions and/or spectral density functions for Sturm-Liouville problems in the form with boundary conditions (at regular points).

I2...... Partial differential equations

I2a.... Initial boundary value problems

I2a1... Parabolic

PDE_1D_MG Integrates an initial-value PDE problem with one space variable.

I2a1a. One spatial dimension

MOLCH Solves a system of partial differential equations of the form ut = f(x, t, u, ux, uxx) using the method of lines. The solution is represented with cubic Hermite polynomials.

I2b.... Elliptic boundary value problems

I2b1... Linear

I2b1a. Second order

I2b1a1 Poisson (Laplace) or Helmholtz equation

I2b1a1a Rectangular domain (or topologically rectangular in the coordinate system)

FPS2H Solves Poisson's or Helmholtz's equation on a two-dimensional rectangle using a fast Poisson solver based on the HODIE finite-difference scheme on a uni mesh.

FPS3H Solves Poisson's or Helmholtz's equation on a three-dimensional box using a fast Poisson solver based on the HODIE finite-difference scheme on a uniform mesh.

J....... INTEGRAL TRANSFORMS

J1...... Trigonometric transforms including fast Fourier transforms

J1a.... One-dimensional

J1a1... Real

FFTRB Computes the real periodic sequence from its Fourier coefficients.

FFTRF Computes the Fourier coefficients of a real periodic sequence.

FFTRI Computes parameters needed by FFTRF and FFTRB.

J1a2... Complex

FAST-DFT Computes the Discrete Fourier Transform (DFT) of a rank-1 complex array, x.

FFTCB Computes the complex periodic sequence from its Fourier coefficients.

FFTCF Computes the Fourier coefficients of a complex periodic sequence.

FFTCI Computes parameters needed by FFTCF and FFTCB.

J1a3... Sine and cosine transforms

FCOSI Computes parameters needed by FCOST.

FCOST Computes the discrete Fourier cosine transformation of an even sequence.

FSINI Computes parameters needed by FSINT.

FSINT Computes the discrete Fourier sine transformation of an odd sequence.

QCOSB Computes a sequence from its cosine Fourier coefficients with only odd wave numbers.

QCOSF Computes the coefficients of the cosine Fourier transform with only odd wave numbers.

QCOSI Computes parameters needed by QCOSF and QCOSB.

QSINB Computes a sequence from its sine Fourier coefficients with only odd wave numbers.

QSINF Computes the coefficients of the sine Fourier transform with only odd wave numbers.

QSINI Computes parameters needed by QSINF and QSINB.

J1b.... Multidimensional

FFT2B Computes the inverse Fourier transform of a complex periodic two-dimensional array.

FFT2D Computes Fourier coefficients of a complex periodic two-dimensional array.

FFT3B Computes the inverse Fourier transform of a complex periodic three-dimensional array.

FFT3F Computes Fourier coefficients of a complex periodic threedimensional array.

FAST_2DFT Computes the Discrete Fourier Transform (DFT) of a rank-2 complex array, x.

FAST_3DFT Computes the Discrete Fourier Transform (DFT) of a rank-3 complex array, x.

J2...... Convolutions

CCONV Computes the convolution of two complex vectors.

RCONV Computes the convolution of two real vectors.

J3...... Laplace transforms

INLAP Computes the inverse Laplace transform of a complex function.

SINLP Computes the inverse Laplace transform of a complex function.

K....... APPROXIMATION (search also class L8)

K1..... Least squares (L2) approximation

K1a.... Linear least squares (search also classes D5, D6, D9)

K1a1.. Unconstrained

K1a1a. Univariate data (curve fitting)

K1a1a1..... Polynomial splines (piecewise polynomials)

BSLSQ Computes the least-squares spline approximation, and return the B-spline coefficients.

BSVLS Computes the variable knot B-spline least squares approximation to given data.

CONFT Computes the least-squares constrained spline approximation, returning the B-spline coefficients.

FRENCH_CURVE Constrained weighted least-squares fitting of B-splines to discrete data, with covariance matrix.and constraints at points.

K1a1a2..... Polynomials

RCURV Fits a polynomial curve using least squares.

K1a1a3..... Other functions (e.g., trigonometric, user-specified)

FNLSQ Compute a least-squares approximation with user-supplied basis functions.

K1a1b. Multivariate data (surface fitting)

BSLS2 Computes a two-dimensional tensor-product spline approximant using least squares, returning the tensor-product B-spline coefficients.

BSLS3 Computes a three-dimensional tensor-product spline approximant using least squares, returning the tensor-product B-spline coefficients.

SURFACE_FAIRING Constrained weighted least-squares fitting of tensor product B-splines to discrete data, with covariance matrix and constraints at points.

K1a2.. Constrained

LIN_SOL_LSQ_CON Routine for constrained linear-least squares based on a                                least-distance, dual algorithm.
LIN_SOL_LSQ_INQ   Routine for constrained linear-least squares based on a                                least-distance, dual algorithm.
LEAST_PROJ_
DISTANCE          Routine for constrained linear-least squares based on a                                least-distance, dual algorithm.

PARALLEL_&
NONONEGATIVE_LSQ Solves multiple systems of linear equations
Ajxj = yj, j = 1, ¼, k. Each matrix Aj is tridiagonal with the same dimension, n: The default solution method is based on LU factorization computed using cyclic reduction. An option is used to select Gaussian elimination with partial pivoting.

PARALLEL_& BOUNDED_LSQ
Parallel routines for simple bounded constrained linear-least squares based on a descent algorithm.

K1a2a. Linear constraints

LCLSQ Solves a linear least-squares problem with linear constraints.

PARALLEL_
NONNEGATIVE_LSQ Solves a large least-squares system with non-negative constraints, using parallel computing.

PARALLEL_
BOUNDED_LSQ Solves a large least-squares system with simple bounds, using parallel computing.

K1b.... Nonlinear least squares

K1b1.. Unconstrained

K1b1a. Smooth functions

K1b1a1..... User provides no derivatives

UNLSF Solves a nonlinear least squares problem using a modified Levenberg-Marquardt algorithm and a finite-difference Jacobian.

K1b1a2..... User provides first derivatives

UNLSJ Solves a nonlinear least squares problem using a modified Levenberg-Marquardt algorithm and a user-supplied Jacobian.

K1b2.. Constrained

K1b2a. Linear constraints

BCLSF Solves a nonlinear least squares problem subject to bounds on the variables using a modified Levenberg-Marquardt algorithm and a finite-difference Jacobian.

BCLSJ Solves a nonlinear least squares problem subject to bounds on the variables using a modified Levenberg-Marquardt algorithm and a user-supplied Jacobian.

BCNLS Solves a nonlinear least-squares problem subject to bounds on the variables and general linear constraints.

K2..... Minimax (L_∞) approximation

RATCH Computes a rational weighted Chebyshev approximation to a continuous function on an interval.

K5..... Smoothing

CSSCV Computes a smooth cubic spline approximation to noisy data using cross-validation to estimate the smoothing parameter.

CSSED Smooths one-dimensional data by error detection.

CSSMH Computes a smooth cubic spline approximation to noisy data.

K6..... Service routines for approximation

K6a.... Evaluation of fitted functions, including quadrature

K6a1.. Function evaluation

BSVAL Evaluates a spline, given its B-spline representation.

CSVAL Evaluates a cubic spline.

PPVAL Evaluates a piecewise polynomial.

K6a2.. Derivative evaluation

BSDER Evaluates the derivative of a spline, given its B-spline representation.

CS1GD Evaluates the derivative of a cubic spline on a grid.

CSDER Evaluates the derivative of a cubic spline.

PP1GD Evaluates the derivative of a piecewise polynomial on a grid.

PPDER Evaluates the derivative of a piecewise polynomial.

K6a3.. Quadrature

CSITG Evaluates the integral of a cubic spline.

PPITG Evaluates the integral of a piecewise polynomial.

K6c.... Manipulation of basis functions (e.g., evaluation, change of basis)

BSCPP Converts a spline in B-spline representation to piecewise polynomial representation.

L....... STATISTICS, PROBABILITY

L1...... Data summarization

L1c.... Multi-dimensional data

L1c1.. Raw data

L1c1b. Covariance, correlation

CCORL Computes the correlation of two complex vectors.

RCORL Computes the correlation of two real vectors.

L3...... Elementary statistical graphics (search also class Q)

L3e.... Multi-dimensional data

L3e3.. Scatter diagrams

L3e3a. Superimposed Y vs. X

PLOTP Prints a plot of up to 10 sets of points.

L6...... Random number generation

L6a.... Univariate

RAND_GEN Generates a rank-1 array of random numbers. The output array entries are positive and less than 1 in value.

L6a21. Uniform (continuous, discrete), uniform order statistics

RNUN Generates pseudorandom numbers from a uniform (0, 1) distribution.

RNUNF Generates a pseudorandom number from a uniform (0, 1) distribution.

L6b.... Mulitivariate

L6b21. Linear L-1 (least absolute value) approximation random numbers

FAURE_INIT Shuffles Faure sequence initialization.

FAURE_FREE Frees the structure containing information about the Faure sequence.

FAURE_NEXT Computes a shuffled Faure sequence.

L6c.... Service routines (e.g., seed)

RNGET Retrieves the current value of the seed used in the IMSL random number generators.

RNOPT Selects the uniform (0, 1) multiplicative congruential pseudorandom number generator.

RNSET Initializes a random seed for use in the IMSL random number generators.

RAND_GEN Generates a rank-1 array of random numbers. The output array entries are positive and less than 1 in value.

L8...... Regression (search also classes D5, D6, D9, G, K)

L8a.... Simple linear (e.g., y = b0 + b1x + e) (search also class L8h)

L8a1.. Ordinary least squares

FNLSQ Computes a least-squares approximation with user-supplied basis functions.

L8a1a. Parameter estimation

L8a1a1. Unweighted data

RLINE Fits a line to a set of data points using least squares.

L8b.... Polynomial (e.g., y = b0 + b1x + b2x2 + e ) (search also class L8c)

L8b1.. Ordinary least squares

L8b1b. Parameter estimation

L8b1b2. Using orthogonal polynomials

RCURV Fits a polynomial curve using least squares.

L8c.... Multiple linear (e.g., y = b0 + b1x1 + ¼ + bkxk + e)

L8c1.. Ordinary least squares

L8c1b. Parameter estimation (search also class L8c1a)

L8c1b1..... Using raw data

LSBRR Solves a linear least-squares problem with iterative refinement.

LSQRR Solves a linear least-squares problem without iterative refinement.

N....... DATA HANDLING

N1..... Input, output

PGOPT Sets or retrieves page width and length for printing.

WRCRL Prints a complex rectangular matrix with a given format and labels.

WRCRN Prints a complex rectangular matrix with integer row and column labels.

WRIRL Prints an integer rectangular matrix with a given format and labels.

WRIRN Prints an integer rectangular matrix with integer row and column labels.

WROPT Sets or retrieves an option for printing a matrix.

WRRRL Prints a real rectangular matrix with a given format and labels.

WRRRN Prints a real rectangular matrix with integer row and column labels.

SCALAPACK_READ Reads matrix data from a file and place in a two-dimensional block-cyclic form on a process grid.

SCALAPACK_WRITE Writes matrix data to a file, starting with a two-dimensional block-cyclic form on a process grid.

SHOW Prints rank-1 and rank-2 arrays with indexing and text.

N3..... Character manipulation

ACHAR Returns a character given its ASCII value.

CVTSI Converts a character string containing an integer number into the corresponding integer form.

IACHAR Returns the integer ASCII value of a character argument.

ICASE Returns the ASCII value of a character converted to uppercase.

IICSR Compares two character strings using the ASCII collating sequence but without regard to case.

IIDEX Determines the position in a string at which a given character sequence begins without regard to case.

N4..... Storage management (e.g., stacks, heaps, trees)

IWKCIN Initializes bookkeeping locations describing the character workspace stack.

IWKIN Initializes bookkeeping locations describing the workspace stack.

ScaLAPACK_READ Moves data from a file to Block-Cyclic form, for use in ScaLAPACK.

ScaLAPACK_WRITE Move data from Block-Cyclic form, following use in ScaLAPACK, to a file.

N5..... Searching

N5b.... Insertion position

ISRCH Searches a sorted integer vector for a given integer and return its index.

SRCH Searches a sorted vector for a given scalar and return its index.

SSRCH Searches a character vector, sorted in ascending ASCII order, for a given string and return its index.

N5c.... On a key

IIDEX Determines the position in a string at which a given character sequence begins without regard to case.

ISRCH Searches a sorted integer vector for a given integer and return its index.

SRCH Searches a sorted vector for a given scalar and return its index.

SSRCH Searches a character vector, sorted in ascending ASCII order, for a given string and return its index.

N6..... Sorting

N6a.... Internal

N6a1.. Passive (i.e., construct pointer array, rank)

N6a1a Integer

SVIBP Sorts an integer array by nondecreasing absolute value and return the permutation that rearranges the array.

SVIGP Sorts an integer array by algebraically increasing value and return the permutation that rearranges the array.

N6a1b Real

SVRBP Sorts a real array by nondecreasing absolute value and return the permutation that rearranges the array.

SVRGP Sorts a real array by algebraically increasing value and return the permutation that rearranges the array.

LIN_SOL_TRI Sorts a rank-1 array of real numbers x so the y results are algebraically nondecreasing, .

N6a2.. Active

N6a2a Integer

SVIBN Sorts an integer array by nondecreasing absolute value.

SVIBP Sorts an integer array by nondecreasing absolute value and return the permutation that rearranges the array.

SVIGN Sorts an integer array by algebraically increasing value.

SVIGP Sorts an integer array by algebraically increasing value and return the permutation that rearranges the array.

N6a2b Real

SVRBN Sorts a real array by nondecreasing absolute value.

SVRBP Sorts a real array by nondecreasing absolute value and return the permutation that rearranges the array.

SVRGN Sorts a real array by algebraically increasing value.

SVRGP Sorts a real array by algebraically increasing value and return the permutation that rearranges the array.

N8..... Permuting

PERMA Permutes the rows or columns of a matrix.

PERMU Rearranges the elements of an array as specified by a permutation.

Q....... GRAPHICS (search also classes L3)

PLOTP Prints a plot of up to 10 sets of points.

R....... SERVICE ROUTINES

IDYWK Computes the day of the week for a given date.

IUMAG Sets or retrieves MATH/LIBRARY integer options.

NDAYS Computes the number of days from January 1, 1900, to the given date.

NDYIN Gives the date corresponding to the number of days since January 1, 1900.

SUMAG Sets or retrieves MATH/LIBRARY single-precision options.

TDATE Get stoday's date.

TIMDY Gets time of day.

VERML Obtains IMSL MATH/LIBRARY-related version, system and license numbers.

R1..... Machine-dependent constants

AMACH Retrieves single-precision machine constants.

IFNAN Checks if a value is NaN (not a number).

IMACH Retrieves integer machine constants.

ISNAN Detects an IEEE NaN (not-a-number).

NAN Returns, as a scalar function, a value corresponding to the IEEE 754 Standard format of floating point (ANSI/IEEE 1985) for NaN.

UMACH Sets or retrieves input or output device unit numbers.

R3..... Error handling

BUILD_ERROR
_STRUCTURE Fills in flags, values and update the data structure for error conditions that occur in Library routines. Prepares the structure so that calls to routine error_post will display the reason for the error.

R3b.... Set unit number for error messages

UMACH Sets or retrieves input or output device unit numbers.

R3c.... Other utilities

ERROR_POST Prints error messages that are generated by IMSL Library routines.

ERSET Sets error handler default print and stop actions.

IERCD Retrieves the code for an informational error.

N1RTY Retrieves an error type for the most recently called IMSL routine.

S....... SOFTWARE DEVELOPMENT TOOLS

S3..... Dynamic program analysis tools

CPSEC Returns CPU time used in seconds.

Visual Numerics, Inc.
Visual Numerics - Developers of IMSL and PV-WAVE
http://www.vni.com/
PHONE: 713.784.3131
FAX:713.781.9260