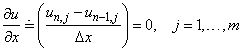Computes the product of the inverse of a matrix and a vector or matrix.
Operator Return Value
Matrix containing the product of A-1 and B. (Output)
Required Operands
A — Left operand matrix. This is an array of rank 2, or 3. It may be real, double, complex, double complex, or one of the computational sparse matrix derived types, ?_hbc_sparse. (Input)
B — Right operand matrix or vector. This is an array of rank 1, 2, or 3. It may be real, double, complex, or double complex. (Input)
Optional Variables, Reserved Names
This operator uses the routines lin_sol_gen or lin_sol_lsq (See Chapter 1, “Linear Systems”).
The option and derived type names are given in the following tables:
For a description on how to use these options, see Matrix Optional Data Changes. See lin_sol_gen and lin_sol_lsq located in Chapter 1, “Linear Systems” for the specific options for these routines.
FORTRAN 90 Interface
Description
Computes the product of the inverse of matrix A and vector or matrix B, for square non-singular matrices or the corresponding Moore-Penrose generalized inverse matrix for singular square matrices or rectangular matrices. The operation may be read generalized inverse times. The results are in a precision and data type that matches the most accurate or complex operand.
.ix. can be used with either dense or sparse matrices. It is MPI capable for dense matrices only.
Examples
Dense Matrix Example (operator_ex01.f90)
! This is the equivalent of Example 1 for LIN_SOL_GEN, with
operators
! and functions.
real(kind(1e0)) :: one=1.0e0, err
real(kind(1e0)), dimension(n,n) :: A, b, x
! Generate random matrices for A and b:
! Compute the solution matrix of Ax = b.
err = norm(b - (A .x. x))/(norm(A)*norm(x)+norm(b))
if (err <= sqrt(epsilon(one))) &
write (*,*) 'Example 1 for LIN_SOL_GEN (operators) is correct.'
real (kind(1.e0)) x(N,N), y(N,N), B(N,N)
if (err <= sqrt(epsilon(one))) then
write (*,*) 'Sparse example for .ix. operator is correct.'
Sparse Matrix Example 2: Plane Poisson Problem with Dirichlet Boundary Conditions
We want to calculate a numerical solution, which
approximates the true solution of the Poisson (boundary value) problem in the
solution domain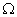 , a
rectangle in
, a
rectangle in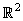 The
equation is
The
equation is
There are Dirichlet boundary conditions 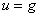 on
on 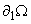
There are further Neumann boundary conditions 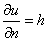 on
on 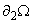
The boundary arcs comprising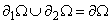 are mutually exclusive of each
other. The functions
are mutually exclusive of each
other. The functions 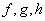 are defined on their respective domains.
are defined on their respective domains.
We will solve an instance of this problem by using finite differences to approximate the derivatives. This will lead to a sparse system of linear algebraic equations. Note that particular cases of this problem can be solved with methods that are likely to be more efficient or more appropriate than the one illustrated here. We use this method to illustrate our matrix data handling routines and defined operators.
The area of the rectangle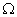 is
is 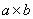 with the origin fixed at the lower
left or SW corner. The dimension along the
with the origin fixed at the lower
left or SW corner. The dimension along the  axis is
axis is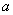 and along the
and along the axis is
axis is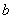 . A rectangular
. A rectangular 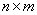 uniform grid is defined on
uniform grid is defined on
 where each sub-rectangle
in the grid has sides
where each sub-rectangle
in the grid has sides 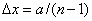 and
and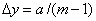 . What is perhaps novel in our development is that the
boundary values are written into the
. What is perhaps novel in our development is that the
boundary values are written into the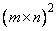 linear system as trivial equations. This leads to more
unknowns than standard approaches to this problem but the complexity of
describing the equations into computer code is reduced. The boundary
conditions are naturally in place when the solution is obtained. No
reshaping is required.
linear system as trivial equations. This leads to more
unknowns than standard approaches to this problem but the complexity of
describing the equations into computer code is reduced. The boundary
conditions are naturally in place when the solution is obtained. No
reshaping is required.
We number the approximate values of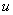 at the grid points and collapse
them into a single vector. Given a coordinate of the grid
at the grid points and collapse
them into a single vector. Given a coordinate of the grid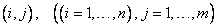 , we use the mapping
, we use the mapping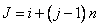 to define coordinate
to define coordinate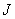 of this vector. This mapping
enables us to define the matrix that is used to solve for the values of
of this vector. This mapping
enables us to define the matrix that is used to solve for the values of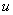 at the grid points.
at the grid points.
For the Neumann boundary conditions we take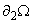 to be the East face of the
rectangle. Along that edge we have
to be the East face of the
rectangle. Along that edge we have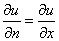 , and we impose the smooth interface
, and we impose the smooth interface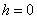 .
.
Our use of finite differences is standard. For the differential equation we approximate
at the inner grid points 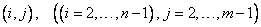 . For the Neumann condition
we approximate
. For the Neumann condition
we approximate
The remaining equations come from the Dirichlet conditions
given on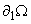 .
.
To illustrate three examples of solutions to this problem
we consider
1. A
Laplace Equation with the boundary conditions
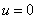 , on the South
Edge
, on the South
Edge
 , on the East
Edge
, on the East
Edge
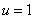 , on the North
Edge
, on the North
Edge
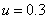 , on the West Edge
, on the West Edge
The
function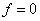 for all
for all . Graphical results are
shown below with the title Problem Case 1
. Graphical results are
shown below with the title Problem Case 1
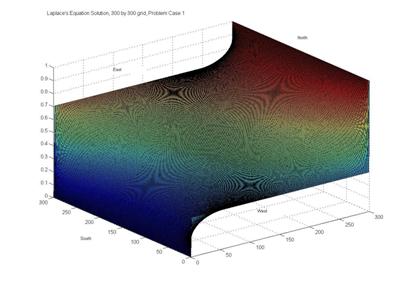
2. A
Poisson equation with the boundary conditions 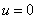 on all of the edges and
on all of the edges and  . This problem has the
solution
. This problem has the
solution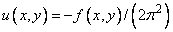 , and this
identity provides a way of verifying that the accuracy is within the truncation
error implied by the difference equations. Graphical results are shown
with the title Problem
Case 2 The residual function verifies the expected accuracy.
, and this
identity provides a way of verifying that the accuracy is within the truncation
error implied by the difference equations. Graphical results are shown
with the title Problem
Case 2 The residual function verifies the expected accuracy.
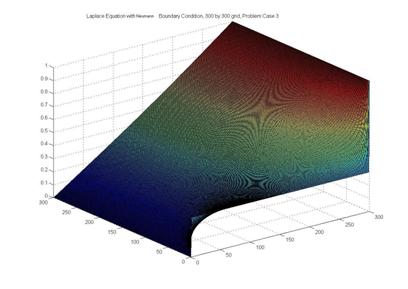
3. The
Laplace Equation with the boundary conditions of Problem Case 1 except that the
boundary condition on the East Edge is replaced by the Neumann
condition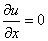 .
Graphical results are shown as Problem Case 3.”
.
Graphical results are shown as Problem Case 3.”
! Illustrate a 2D Poisson equation with Dirichlet and
! Neumann boundary conditions.
! These modules defines the structures and overloaded assignment code.
Integer :: I, J, JJ, MY_CASE, IFILE
Integer, Parameter :: N = 300, M = 300
Real (Kind(1.d0)) :: a = 1.d0, b = 1.d0
Real (Kind(1.d0)) :: delx, dely, r, s, pi, scale
Real (Kind(1.d0)) :: u(N*M), w(N*M), P(N, M)
CHARACTER(LEN=12) :: PR_LABEL(3)=&
(/'Laplace','Poisson','Neumann'/)
! Mapping function (in-line) for grid coordinate to
! Define sparse matrices to hold problem data.
! Define differences and related parameters.
! 1. Solve boundary value problem with f=0 and Dirichlet
! 2. Solve Poisson equation with f such that a solution is known.
! Use zero boundary condtions.
! 3. Solve boundary value problem with Dirichlet condtions as in 1.
! except on the East edge. There the partial WRT x is zero.
! Set timer for building the matrix.
! Write entries for second partials WRT x and y.
C = d_entry (JJ(I, J), JJ(I-1, J), r)
C = d_entry (JJ(I, J), JJ(I+1, J), r)
C = d_entry (JJ(I, J), JJ(I, J),-2*(r+s))
C = d_entry (JJ(I, J), JJ(I, J-1), s)
C = d_entry (JJ(I, J), JJ(I, J+1), s)
! Define components of the right-hand side.
w (JJ(I, J)) = f((I-1)*delx, (J-1)*dely, MY_CASE)
! Write entries for Dirichlet boundary conditions.
! First do the South edge, then the West, then the North.
C = d_entry (JJ(I, 1), JJ(I, 1), r+s)
w (JJ(I, 1)) = g ((I-1)*delx, 0.d0, MY_CASE) * (r+s)
C = d_entry (JJ(1, J), JJ(1, J), r+s)
w (JJ(1, J)) = g (0.d0, (J-1)*dely, MY_CASE) * (r+s)
C = d_entry (JJ(I, M), JJ(I, M), r+s)
w (JJ(I, M)) = g ((I-1)*delx, b, MY_CASE) * (r+s)
C = d_entry (JJ(N, J), JJ(N, J), (r+s))
w (JJ(N, J)) = g (a, (J-1)*dely, MY_CASE) * (r+s)
! Write entries for the boundary values but avoid the East edge.
C = d_entry (JJ(I, 1), JJ(I, 1), r+s)
w (JJ(I, 1)) = g ((I-1)*delx, 0.d0, MY_CASE) * (r+s)
C = d_entry (JJ(1, J), JJ(1, J), r+s)
w (JJ(1, J)) = g (0.d0, (J-1)*dely, MY_CASE) * (r+s)
C = d_entry (JJ(I, M), JJ(I, M), r+s)
w (JJ(I, M)) = g ((I-1)*delx, b, MY_CASE) * (r+s)
! Write entries for the Neumann condition on the East edge.
C = d_entry (JJ(N, J), JJ(N, J), 1.d0/delx)
C = d_entry (JJ(N, J), JJ(N-2, J),-1.d0/delx)
! Convert to Harwell-Boeing format for solving.
Write (*,'(A,F6.2," S. - ",A)') "Time to build matrix = ", &
! Turn off iterative refinement for maximal performance.
! This is generally not recommended unless
! the problem is known not to require it.
If (MY_CASE == 2) D%options%iterRefine = 0
Write (*,'(A,I6," is",F6.2," S")') &
"Time to solve system of size = ", N * M, TE - TS
! This is a second solve step using the factorization
Write (*,'(A,I6," is",F6.2," S")') &
"Time for a 2nd system of size (iterative refinement) =", &
Write (*,'(A,I6," is",F6.2," S")') &
"Time for a 2nd system of size (without refinement) =", &
! Convert solution vector to a 2D array of values.
! This uses the known form of the solution to compute residuals.
P (I, J) = P (I, J) - scale * f ((I-1)*delx, &
write (*,*) minval (P), " = min solution error "
write (*,*) maxval (P), " = max solution error "
Write (*,'(A,1pE12.4/)') "Condition number of matrix", cond (D)
! Clear all matrix data for next problem case.
! Define the right-hand side function associated with the
! Define the edge values, except along East edge, x = a.
! Fill in a constant value along each edge.
If (MY_CASE == 1 .Or. MY_CASE == 3) Then
Parallel Example (parallel_ex01.f90)
! This is the equivalent of Parallel Example 1 for .ix., with box data types
integer, parameter :: n=32, nr=4
real(kind(1e0)), dimension(n,n,nr) :: A, b, x, err(nr)
! Generate random matrices for A and b:
! Compute the box solution matrix of Ax = b.
err = norm(b - (A .x. x))/(norm(A)*norm(x)+norm(b))
if (ALL(err <= sqrt(epsilon(one))) .and. MP_RANK == 0) &
write (*,*) 'Parallel Example 1 is correct.'
! See to any error messages and quit MPI.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |

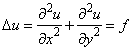 in
in