Downdates the RT R Cholesky factorization of a real symmetric positive definite matrix after a rank-one matrix is removed.

Required Arguments

R — N by N upper triangular matrix containing the upper triangular factor to be downdated.   (Input)
Only the upper triangle of R is referenced.

X — Vector of length N determining the rank-one matrix to be subtracted from the factorization RT R.   (Input)

RNEW — N by N upper triangular matrix containing the downdated triangular factor of
RT R − X XT.   (Output)
Only the upper triangle of RNEW is referenced. If R is not needed, R and RNEW can share the same storage locations.

Optional Arguments

N — Order of the matrix.   (Input)
Default: N = size (R,2).

LDR — Leading dimension of R exactly as specified in the dimension statement of the calling program.   (Input)
Default: LDR = size (R,1).

LDRNEW — Leading dimension of RNEW exactly as specified in the dimension statement of the calling program.   (Input)
Default: LDRNEW = size (RNEW,1).

CS — Vector of length N containing the cosines of the rotations.   (Output)

SN — Vector of length N containing the sines of the rotations.   (Output)

FORTRAN 90 Interface

Generic:                              CALL LDNCH (R, X, RNEW [,…])

Specific:                             The specific interface names are S_LDNCH and D_LDNCH.

FORTRAN 77 Interface

Single:            CALL LDNCH (N, R, LDR, X, RNEW, LDRNEW, CS, SN)

Double:                              The double precision name is DLDNCH.

Description

The routine LDNCH is based on the LINPACK routine SCHDD; see Dongarra et al. (1979).

The Cholesky factorization of a matrix is A = RT R, where R is an upper triangular matrix. Given this factorization, LDNCH computes the factorization

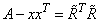
In the program

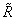
is called RNEW. This is not always possible, since A − xxT may not be positive definite.

LDNCH determines an orthogonal matrix U as the product GN …G1of Givens rotations, such that

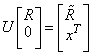
By multiplying this equation by its transpose and noting that UT U = I, the desired result

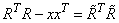
is obtained.

Let a be the solution of the linear system RT a = x and let

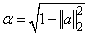
The Givens rotations, Gi, are chosen such that

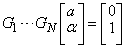
The Gi are (N + 1) × (N + 1) matrices of the form

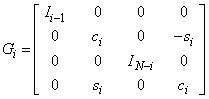
where Ik is the identity matrix of order k; and ci= cosθi = CS(I), si= sinθi = SN(I) for some θi.

The Givens rotations are then used to form

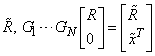
The matrix

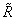
is upper triangular and

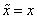
because

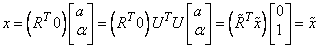
Comments

            Informational error

Type   Code

4           1                  RTR − X XT is not positive definite. R cannot be downdated.

Example

A linear system Az = b is solved using the Cholesky factorization of A. This factorization is then downdated, and the system (A − xxT)z = b is solved using this downdated factorization.

 

      USE LDNCH_INT
      USE LFTDS_INT
      USE LFSDS_INT
      USE WRRRN_INT
!                                 Declare variables

      INTEGER    LDA, LDFACT, N

      PARAMETER  (LDA=3, LDFACT=3, N=3)

      REAL       A(LDA,LDA), FACT(LDFACT,LDFACT), FACNEW(LDFACT,LDFACT), &

                X(N), B(N), CS(N), SN(N), Z(N)

!

!                                 Set values for A

!                                 A = ( 10.0   3.0   5.0)

!                                     (  3.0  14.0  -3.0)

!                                     (  5.0  -3.0   7.0)

!

      DATA A/10.0, 3.0, 5.0, 3.0, 14.0, -3.0, 5.0, -3.0, 7.0/

!

!                                 Set values for X and B

      DATA X/3.0, 2.0, 1.0/

      DATA B/53.0, 20.0, 31.0/

!                                 Factor the matrix A

      CALL LFTDS (A, FACT)

!                                 Solve the original system

      CALL LFSDS (FACT, B, Z)

!                                 Print the results

      CALL WRRRN ('FACT', FACT, ITRING=1)

      CALL WRRRN ('Z', Z, 1, N, 1)

!                                 Downdate the factorization

      CALL LDNCH (FACT, X, FACNEW)

!                                 Solve the updated system

      CALL LFSDS (FACNEW, B, Z)

!                                 Print the results

      CALL WRRRN ('FACNEW', FACNEW, ITRING=1)

      CALL WRRRN ('Z', Z, 1, N, 1)

!

      END

Output

 

          FACT
        1       2       3
1   3.162   0.949   1.581
2           3.619  -1.243
3                   1.719

            Z

      1       2       3

  4.000   1.000   2.000

          FACNEW

        1       2       3

1   1.000  -3.000   2.000

2           1.000   1.000

3                   1.000

             Z

     1        2        3

1859.9    433.0   -254.0

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260