LSVRR

Computes the singular value decomposition of a real matrix.

Required Arguments

A — NRA by NCA matrix whose singular value decomposition is to be computed. (Input)

IPATH — Flag used to control the computation of the singular vectors. (Input)
IPATH has the decimal expansion IJ such that:
I = 0 means do not compute the left singular vectors;
I = 1 means return the NRA left singular vectors in U;
NOTE: This option is not available for the ScaLAPACK interface. If this option is chosen for ScaLAPACK usage, the min(NRA, NCA) left singular vectors will be returned.
I = 2 means return only the min(NRA, NCA) left singular vectors in U;
J = 0 means do not compute the right singular vectors,
J = 1 means return the right singular vectors in V.

For example, IPATH = 20 means I = 2 and J = 0.

S — Vector of length min(NRA + 1, NCA) containing the singular values of A in descending order of magnitude in the first min(NRA, NCA) positions. (Output)

Optional Arguments

NRA — Number of rows in the matrix A. (Input)
Default: NRA = size (A,1).

NCA — Number of columns in the matrix A. (Input)
Default: NCA = size (A,2).

LDA — Leading dimension of A exactly as specified in the dimension statement of the calling program. (Input)
Default: LDA = size (A,1).

TOL — Scalar containing the tolerance used to determine when a singular value is negligible. (Input)
If TOL is positive, then a singular value σi considered negligible if σi ≤ TOL . If TOL is negative, then a singular value σi considered negligible if σi ≤ |TOL| * ||A||∞. In this case, |TOL| generally contains an estimate of the level of the relative error in the data.
Default: TOL = 1.0e-5 for single precision and 1.0d-10 for double precision.

IRANK — Scalar containing an estimate of the rank of A. (Output)

U — NRA by NCU matrix containing the left singular vectors of A. (Output)
NCU must be equal to NRA if I is equal to 1. NCU must be equal to min(NRA, NCA) if I is equal to 2. U will not be referenced if I is equal to zero. If NRA is less than or equal to NCU, then U can share the same storage locations as A. See Comments.

LDU — Leading dimension of U exactly as specified in the dimension statement of the calling program. (Input)
Default: LDU = size (U,1).

V — NCA by NCA matrix containing the right singular vectors of A. (Output)
V will not be referenced if J is equal to zero. V can share the same storage location as A, however, U and V cannot both coincide with A simultaneously.

LDV — Leading dimension of V exactly as specified in the dimension statement of the calling program. (Input)
Default: LDV = size (V,1).

FORTRAN 90 Interface

Generic: CALL LSVRR (A, IPATH, S [ ,…])

Specific: The specific interface names are S_LSVRR and D_LSVRR.

FORTRAN 77 Interface

Single: CALL LSVRR (NRA, NCA, A, LDA, IPATH, TOL, IRANK, S, U, LDU, V, LDV)

Double: The double precision name is DLSVRR.

ScaLAPACK Interface

Generic: CALL LSVRR (A0, IPATH, S [,…])

Specific: The specific interface names are S_LSVRR and D_LSVRR.

See the ScaLAPACK Usage Notes below for a description of the arguments for distributed computing.

Description

The underlying code of routine LSVRR is based on either LINPACK , LAPACK, or ScaLAPACK code depending upon which supporting libraries are used during linking. For a detailed explanation see “Using ScaLAPACK, LAPACK, LINPACK, and EISPACK” in the Introduction section of this manual.

Let n = NRA (the number of rows in A) and let p = NCA (the number of columns in A). For any n × p matrix A, there exists an n × n orthogonal matrix U and a p × p orthogonal matrix V such that

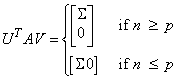
where ∑ = diag(σ1, …, σm), and m = min(n, p). The scalars σ1 ≥ σ2 ≥… ≥ σm ≥ 0 are called the singular values of A. The columns of U are called the left singular vectors of A. The columns of V are called the right singular vectors of A.

The estimated rank of A is the number of σk that is larger than a tolerance η. If τ is the parameter TOL in the program, then

Comments

1. Workspace may be explicitly provided, if desired, by use of L2VRR/DL2VRR. The reference is:

CALL L2VRR (NRA, NCA, A, LDA, IPATH, TOL, IRANK, S, U, LDU, V, LDV,
ACOPY, WK)

The additional arguments are as follows:

ACOPY — NRA × NCA work array for the matrix A. If A is not needed, then A and ACOPY may share the same storage locations.

WK — Work vector of length NRA + NCA + max(NRA, NCA) − 1.

2. Informational error

Type Code

4 1 Convergence cannot be achieved for all the singular values and their corresponding singular vectors.

3. When NRA is much greater than NCA, it might not be reasonable to store the whole matrix U. In this case, IPATH with I = 2 allows a singular value factorization of A to be computed in which only the first NCA columns of U are computed, and in many applications those are all that are needed.

4. Integer Options with Chapter 11 Options Manager

16 This option uses four values to solve memory bank conflict (access inefficiency) problems. In routine L2VRR the leading dimension of ACOPY is increased by IVAL(3) when N is a multiple of IVAL(4). The values IVAL(3) and IVAL(4) are temporarily replaced by IVAL(1) and IVAL(2), respectively, in LSVRR. Additional memory allocation for ACOPY and option value restoration are done automatically in LSVRR. Users directly calling L2VRR can allocate additional space for ACOPY and set IVAL(3) and IVAL(4) so that memory bank conflicts no longer cause inefficiencies. There is no requirement that users change existing applications that use LSVRR or L2VRR. Default values for the option are
IVAL(*) = 1, 16, 0, 1.

17 This option has two values that determine if the L1 condition number is to be computed. Routine LSVRR temporarily replaces IVAL(2) by IVAL(1). The routine L2CRG computes the condition number if IVAL(2) = 2. Otherwise L2CRG skips this computation. LSVRR restores the option. Default values for the option are IVAL(*) = 1, 2.

ScaLAPACK Usage Notes

The arguments which differ from the standard version of this routine are:

A0 — MXLDA by MXCOL local matrix containing the local portions of the distributed matrix A. A contains the matrix whose singular value decomposition is to be computed. (Input)

U0 — MXLDU by MXCOLU local matrix containing the local portions of the left singular vectors of the distributed matrix A. (Output)
U0 will not be referenced if I is equal to zero. If NRA is less than or equal to NCU, then U0 can share the same storage locations as A0. See Comments.

V0 — MXLDV by MXCOLV local matrix containing the local portions of the right singular vectors of the distributed matrix A. (Output)
V0 will not be referenced if J is equal to zero. V0 can share the same storage location as A0, however, U0 and V0 cannot both coincide with A0 simultaneously.

All other arguments are global and are the same as described for the standard version of the routine. In the argument descriptions above, MXLDA, MXCOL, MXLDU, MXCOLU, MXLDV and MXCOLV can be obtained through a call to ScaLAPACK_GETDIM (see Chapter 11, “Utilities”) after a call to ScaLAPACK_SETUP (see Chapter 11, “Utilities”) has been made. See the ScaLAPACK Example below.

Example

This example computes the singular value decomposition of a 6 × 4 matrix A. The matrices U and V containing the left and right singular vectors, respectively, and the diagonal of ∑, containing singular values, are printed. On some systems, the signs of some of the columns of U and V may be reversed.

USE IMSL_LIBRARIES
! Declare variables

PARAMETER (NRA=6, NCA=4, LDA=NRA, LDU=NRA, LDV=NCA)

REAL A(LDA,NCA), U(LDU,NRA), V(LDV,NCA), S(NCA)

! Set values for A

! A = ( 1 2 1 4 )

! ( 3 2 1 3 )

! ( 4 3 1 4 )

! ( 2 1 3 1 )

! ( 1 5 2 2 )

! ( 1 2 2 3 )

DATA A/1., 3., 4., 2., 1., 1., 2., 2., 3., 1., 5., 2., 3*1., &

3., 2., 2., 4., 3., 4., 1., 2., 3./

! Compute all singular vectors

IPATH = 11

TOL = AMACH(4)

TOL = 10.*TOL

CALL LSVRR(A, IPATH, S, TOL=TOL, IRANK=IRANK, U=U, V=V)

! Print results

CALL UMACH (2, NOUT)

WRITE (NOUT, *) 'IRANK = ', IRANK

CALL WRRRN ('U', U, NRA, NCA)

CALL WRRRN ('S', S, 1, NCA, 1)

CALL WRRRN ('V', V)

END

Output

IRANK = 4

1 2 3 4

1 -0.3805 0.1197 0.4391 -0.5654

2 -0.4038 0.3451 -0.0566 0.2148

3 -0.5451 0.4293 0.0514 0.4321

4 -0.2648 -0.0683 -0.8839 -0.2153

5 -0.4463 -0.8168 0.1419 0.3213

6 -0.3546 -0.1021 -0.0043 -0.5458

1 2 3 4

11.49 3.27 2.65 2.09

1 2 3 4

1 -0.4443 0.5555 -0.4354 0.5518

2 -0.5581 -0.6543 0.2775 0.4283

3 -0.3244 -0.3514 -0.7321 -0.4851

4 -0.6212 0.3739 0.4444 -0.5261

ScaLAPACK Example

The previous example is repeated here as a distributed example. This example computes the singular value decomposition of a 6 × 4 matrix A. The matrices U and V containing the left and right singular vectors, respectively, and the diagonal of S, containing singular values, are printed. On some systems, the signs of some of the columns of U and V may be reversed..

      USE MPI_SETUP_INT
      USE IMSL_LIBRARIES
      USE SCALAPACK_SUPPORT
      IMPLICIT NONE
      INCLUDE ‘mpif.h'

! Declare variables

      INTEGER        KBASIS, LDA, LDQR, NCA, NRA, DESCA(9), DESCU(9), &
                    DESCV(9), MXLDV, MXCOLV, NSZ, MXLDU, MXCOLU
      INTEGER       INFO, MXCOL, MXLDA, LDU, LDV, IPATH, IRANK
      REAL          TOL, AMACH
      REAL, ALLOCATABLE ::        A(:,:),U(:,:), V(:,:), S(:)
      REAL, ALLOCATABLE ::        A0(:,:), U0(:,:), V0(:,:), S0(:)

PARAMETER (NRA=6, NCA=4, LDA=NRA, LDU=NRA, LDV=NCA)

NSZ = MIN(NRA,NCA)

! Set up for MPI

      MP_NPROCS = MP_SETUP()
      IF(MP_RANK .EQ. 0) THEN
          ALLOCATE (A(LDA,NCA), U(LDU,NCA), V(LDV,NCA), S(NCA))

! Set values for A

          A(1,:) = (/ 1.0, 2.0, 1.0, 4.0/)
          A(2,:) = (/ 3.0, 2.0, 1.0, 3.0/)
          A(3,:) = (/ 4.0, 3.0, 1.0, 4.0/)
          A(4,:) = (/ 2.0, 1.0, 3.0, 1.0/)

A(5,:) = (/ 1.0, 5.0, 2.0, 2.0/)

A(6,:) = (/ 1.0, 2.0, 2.0, 3.0/)

ENDIF

! Set up a 1D processor grid and define

! its context ID, MP_ICTXT

CALL SCALAPACK_SETUP(NRA, NCA, .TRUE., .TRUE.)

! Get the array descriptor entities MXLDA,

! MXCOL, MXLDU, MXCOLU, MXLDV, AND MXCOLV

CALL SCALAPACK_GETDIM(NRA, NCA, MP_MB, MP_NB, MXLDA, MXCOL)

CALL SCALAPACK_GETDIM(NRA, NSZ, MP_MB, MP_NB, MXLDU, MXCOLU)

CALL SCALAPACK_GETDIM(NSZ, NCA, MP_MB, MP_NB, MXLDV, MXCOLV)

! Set up the array descriptors

CALL DESCINIT(DESCA, NRA, NCA, MP_MB, MP_NB, 0, 0, MP_ICTXT, &
MXLDA, INFO)

CALL DESCINIT(DESCU, NRA, NSZ, MP_MB, MP_NB, 0, 0, MP_ICTXT, &
MXLDU, INFO)

CALL DESCINIT(DESCV, NSZ, NCA, MP_MB, MP_NB, 0, 0, MP_ICTXT, &
MXLDV, INFO)

! Allocate space for the local arrays

ALLOCATE (A0(MXLDA,MXCOL), U0(MXLDU,MXCOLU), V0(MXLDV,MXCOLV), S(NCA))

! Map input array to the processor grid

CALL SCALAPACK_MAP(A, DESCA, A0)

! Compute all singular vectors

IPATH = 11

TOL = AMACH(4)

TOL = 10. * TOL

CALL LSVRR (A0, IPATH, S, TOL=TOL, IRANK=IRANK, U=U0, V=V0)

! Unmap the results from the distributed

! array back to a non-distributed array.

! After the unmap, only Rank=0 has the full

! array.

CALL SCALAPACK_UNMAP(U0, DESCU, U)

CALL SCALAPACK_UNMAP(V0, DESCV, V)

! Print results.

! Only Rank=0 has the solution.

IF(MP_RANK .EQ. 0) THEN

CALL WRRRN ('U', U, NRA, NCA)

CALL WRRRN ('S', S, 1, NCA, 1)

CALL WRRRN ('V', V)

ENDIF

! Exit ScaLAPACK usage

CALL SCALAPACK_EXIT(MP_ICTXT)

! Shut down MPI

MP_NPROCS = MP_SETUP(‘FINAL')
END

Output

IRANK = 4

1 2 3 4

1 -0.3805 0.1197 0.4391 -0.5654

2 -0.4038 0.3451 -0.0566 0.2148

3 -0.5451 0.4293 0.0514 0.4321

4 -0.2648 -0.0683 -0.8839 -0.2153

5 -0.4463 -0.8168 0.1419 0.3213

6 -0.3546 -0.1021 -0.0043 -0.5458

1 2 3 4

11.49 3.27 2.65 2.09

1 2 3 4

1 -0.4443 0.5555 -0.4354 0.5518

2 -0.5581 -0.6543 0.2775 0.4283

3 -0.3244 -0.3514 -0.7321 -0.4851

4 -0.6212 0.3739 0.4444 -0.5261

Visual Numerics, Inc.
Visual Numerics - Developers of IMSL and PV-WAVE
http://www.vni.com/
PHONE: 713.784.3131
FAX:713.781.9260