Solves a rectangular least-squares system of linear equations Ax ≅ b using singular value decomposition
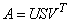
With optional arguments, any of several related computations can be performed. These extra tasks include computing the rank of A, the orthogonal m × m and n × n matrices U and V, and the m × n diagonal matrix of singular values, S.
Required Arguments
A — Array of size m × n containing the
matrix. (Input [/Output])
If the packaged option lin_sol_svd_overwrite_input
is used, this array is not saved on output.
B — Array of size m × nb containing the
right-hand side matrix. (Input [/Output]
If the packaged option lin_sol_svd_overwrite_input
is used, this array is not saved on output.
X— Array of size n × nb containing the solution matrix. (Output)
Optional Arguments
MROWS = m
(Input)
Uses array A(1:m, 1:n) for the input
matrix.
Default: m = size (A, 1)
NCOLS = n
(Input)
Uses array A(1:m, 1:n) for the input
matrix.
Default: n = size(A, 2)
NRHS = nb
(Input)
Uses the array b(1:, 1:nb) for the input
right-hand side matrix.
Default: nb = size(b, 2)
Note that
b must be a
rank-2 array.
RANK = k
(Output)
Number of singular values that are at least as large as the value
Small. It will satisfy k <= min(m, n).
u =
u(:,:) (Output)
Array of the same type and kind as A(1:m, 1:n). It contains the
m × m
orthogonal matrix U of the singular value decomposition.
s =
s(:) (Output)
Array of the same precision as A(1:m, 1:n). This array is
real even when the matrix data is complex. It contains the m × n diagonal matrix
S in a rank-1 array. The singular values are nonnegative and ordered
non-increasing.
v =
v(:,:) (Output)
Array of the same type and kind as A(1:m, 1:n). It contains the
n × n
orthogonal matrix V.
iopt =
iopt(:) (Input)
Derived type array with the same precision
as the input matrix. Used for passing optional data to the routine. The options
are as follows:
|
Packaged Options for lin_sol_svd |
| ||
|
Option Prefix = ? |
Option Name |
Option Value | |
|
s_, d_, c_, z_ |
lin_sol_svd_set_small |
1 | |
|
s_, d_, c_, z_ |
lin_sol_svd_overwrite_input |
2 | |
|
s_, d_, c_, z_ |
lin_sol_svd_safe_reciprocal |
3 | |
|
s_, d_, c_, z_ |
lin_sol_svd_scan_for_NaN |
4 | |
iopt(IO) =
?_options(?_lin_sol_svd_set_small, Small)
Replaces with
zero a diagonal term of the matrix S if it is smaller in magnitude than
the value Small. This determines the approximate rank of the matrix,
which is returned as the “rank=” optional argument. A
solution is approximated based on this replacement.
Default: the smallest
number that can be safely reciprocated
iopt(IO) =
?_options(?_lin_sol_svd_overwrite_input,?_dummy)
Does not save the
input arrays A(:,:) and b(:,:).
iopt(IO) =
?_options(?_lin_sol_svd_safe_reciprocal, safe)
Replaces a
denominator term with safe if it is smaller in magnitude than the value
safe.
Default: the smallest number that can be safely
reciprocated
iopt(IO) =
?_options(?_lin_sol_svd_scan_for_NaN, ?_dummy)
Examines each input
array entry to find the first value such that
isNaN(a(i,j)) .or. isNan(b(i,j)) ==.true.
See the isNaN() function, Chapter 10.
Default: Does not scan for NaNs
FORTRAN 90 Interface
Generic: CALL LIN_SOL_SVD (A, B, X [,…])
Specific: The specific interface names are S_LIN_SOL_SVD, D_LIN_SOL_SVD, C_LIN_SOL_SVD, and Z_LIN_SOL_SVD.
Description
Routine LIN_SOL_SVD solves a rectangular system of linear algebraic equations in a least-squares sense. It computes the factorization of A known as the singular value decomposition. This decomposition has the following form:
A = USVT
The matrices U and V are orthogonal. The matrix S is diagonal with the diagonal terms non-increasing. See Golub and Van Loan (1989, Chapters 5.4 and 5.5) for further details.
Fatal, Terminal, and Warning Error Messages
See the messages.gls file for error messages for LIN_SOL_SVD. These error messages are numbered 401-412; 421-432; 441-452; 461-472.
Example 1: Least-squares solution of a Rectangular System
The least-squares solution of a rectangular m × n system Ax ≅ b is obtained. The use of lin_sol_lsq is more efficient in this case since the matrix is of full rank. This example anticipates a problem where the matrix A is poorly conditioned or not of full rank; thus, lin_sol_svd is the appropriate routine. Also, see operator_ex13, Chapter 10.
use lin_sol_svd_int
use rand_gen_int
implicit none
! This is Example 1 for LIN_SOL_SVD.
integer, parameter :: m=128, n=32
real(kind(1d0)), parameter :: one=1d0
real(kind(1d0)) A(m,n), b(m,1), x(n,1), y(m*n), err
! Generate a random matrix and right-hand side.
call rand_gen(y)
A = reshape(y,(/m,n/))
call rand_gen(b(1:m,1))
! Compute the least-squares solution matrix of Ax=b.
call lin_sol_svd(A, b, x)
! Check that the residuals are orthogonal to the
! column vectors of A.
err = sum(abs(matmul(transpose(A),b-matmul(A,x))))/sum(abs(A))
if (err <= sqrt(epsilon(one))) then
write (*,*) 'Example 1 for LIN_SOL_SVD is correct.'
end if
end
Output
Example 1 for LIN_SOL_SVD is correct.
Additional Examples
.p>.F90CH1.DOC!EX2_LIN_SOL_SVD;Example 2: Polar Decomposition of a Square Matrix
A polar decomposition of an n × n random matrix is
obtained. This decomposition satisfies
A = PQ, where P
is orthogonal and Q is self-adjoint and positive definite.
Given the singular value decomposition
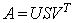
the polar decomposition follows from the matrix products
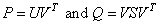
This example uses the optional arguments “u=”, “s=”, and “v=”, then array intrinsic functions to calculate P and Q. Also, see operator_ex14, Chapter 10.
use lin_sol_svd_int
use rand_gen_int
implicit none
! This is Example 2 for LIN_SOL_SVD.
integer i
integer, parameter :: n=32
real(kind(1d0)), parameter :: one=1.0d0, zero=0.0d0
real(kind(1d0)) a(n,n), b(n,0), ident(n,n), p(n,n), q(n,n), &
s_d(n), u_d(n,n), v_d(n,n), x(n,0), y(n*n)
! Generate a random matrix.
call rand_gen(y)
a = reshape(y,(/n,n/))
! Compute the singular value decomposition.
call lin_sol_svd(a, b, x, nrhs=0, s=s_d, &
u=u_d, v=v_d)
! Compute the (left) orthogonal factor.
p = matmul(u_d,transpose(v_d))
! Compute the (right) self-adjoint factor.
q = matmul(v_d*spread(s_d,1,n),transpose(v_d))
ident=zero
do i=1, n
ident(i,i) = one
end do
! Check the results.
if (sum(abs(matmul(p,transpose(p)) - ident))/sum(abs(p)) &
<= sqrt(epsilon(one))) then
if (sum(abs(a - matmul(p,q)))/sum(abs(a)) &
<= sqrt(epsilon(one))) then
write (*,*) 'Example 2 for LIN_SOL_SVD is correct.'
end if
end if
end
Output
Example 2 for LIN_SOL_SVD is correct.
.p>.F90CH1.DOC!EX3_LIN_SOL_SVD;Example 3: Reduction of an Array of Black and White
An n × n array A contains entries that are either 0 or 1. The entry is chosen so that as a two-dimensional object with origin at the point (1, 1), the array appears as a black circle of radius n/4 centered at the point (n/2, n/2).
A singular value decomposition
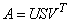
is computed, where S is of low rank. Approximations using fewer of these nonzero singular values and vectors suffice to reconstruct A. Also, see operator_ex15, supplied with the product examples.
use lin_sol_svd_int
use rand_gen_int
use error_option_packet
implicit none
! This is Example 3 for LIN_SOL_SVD.
integer i, j, k
integer, parameter :: n=32
real(kind(1e0)), parameter :: half=0.5e0, one=1e0, zero=0e0
real(kind(1e0)) a(n,n), b(n,0), x(n,0), s(n), u(n,n), &
v(n,n), c(n,n)
! Fill in value one for points inside the circle.
a = zero
do i=1, n
do j=1, n
if ((i-n/2)**2 + (j-n/2)**2 <= (n/4)**2) a(i,j) = one
end do
end do
! Compute the singular value decomposition.
call lin_sol_svd(a, b, x, nrhs=0,&
s=s, u=u, v=v)
! How many terms, to the nearest integer, exactly
! match the circle?
c = zero; k = count(s > half)
do i=1, k
c = c + spread(u(1:n,i),2,n)*spread(v(1:n,i),1,n)*s(i)
if (count(int(c-a) /= 0) == 0) exit
end do
if (i < k) then
write (*,*) 'Example 3 for LIN_SOL_SVD is correct.'
end if
end
Output
Example 3 for LIN_SOL_SVD is correct.
.p>.F90CH1.DOC!EX4_LIN_SOL_SVD;Example 4: Laplace Transform Solution
This example illustrates the solution of a linear least-squares system where the matrix is poorly conditioned. The problem comes from solving the integral equation:
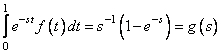
The unknown function f(t) = 1 is computed.
This problem is equivalent to the numerical inversion of the Laplace Transform
of the function g(s) using real values of t and s,
solving for a function that is nonzero only on the unit interval. The
evaluation of the integral uses the following
approximate integration
rule:
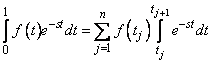
The points 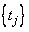 are chosen equally spaced by using the following:
are chosen equally spaced by using the following:
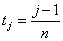
The points 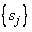 are computed so that the range of g(s) is
uniformly sampled. This requires the
are computed so that the range of g(s) is
uniformly sampled. This requires the
solution of m equations
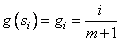
for j = 1, …, n and i = 1, …,
m. Fortran 90 array operations are used to solve for the collocation
points 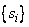 as a single
series of steps. Newton's method,
as a single
series of steps. Newton's method,
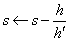
is applied to the array function
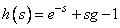
where the following is true:
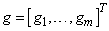
Note the coefficient matrix for the solution values
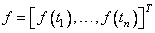
whose entry at the intersection of row i and column j is equal to the value
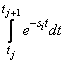
is explicitly integrated and evaluated as an array operation. The solution analysis of the resulting linear least-squares system
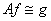
is obtained by computing the singular value decomposition
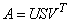
An approximate solution is computed with the transformed right-hand side
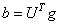
followed by using as few of the largest singular values as possible to minimize the following squared error residual:
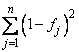
This determines an optimal value k to use in the approximate solution
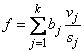
Also, see operator_ex16, supplied with the product examples.
use lin_sol_svd_int
use rand_gen_int
use error_option_packet
implicit none
! This is Example 4 for LIN_SOL_SVD.
integer i, j, k
integer, parameter :: m=64, n=16
real(kind(1e0)), parameter :: one=1e0, zero=0.0e0
real(kind(1e0)) :: g(m), s(m), t(n+1), a(m,n), b(m,1), &
f(n,1), U_S(m,m), V_S(n,n), S_S(n), &
rms, oldrms
real(kind(1e0)) :: delta_g, delta_t
delta_g = one/real(m+1,kind(one))
! Compute which collocation equations to solve.
do i=1,m
g(i)=i*delta_g
end do
! Compute equally spaced quadrature points.
delta_t =one/real(n,kind(one))
do j=1,n+1
t(j)=(j-1)*delta_t
end do
! Compute collocation points.
s=m
solve_equations: do
s=s-(exp(-s)-(one-s*g))/(g-exp(-s))
if (sum(abs((one-exp(-s))/s - g)) <= &
epsilon(one)*sum(g)) &
exit solve_equations
end do solve_equations
! Evaluate the integrals over the quadrature points.
a = (exp(-spread(t(1:n),1,m)*spread(s,2,n)) &
- exp(-spread(t(2:n+1),1,m)*spread(s,2,n))) / &
spread(s,2,n)
b(1:,1)=g
! Compute the singular value decomposition.
call lin_sol_svd(a, b, f, nrhs=0, &
rank=k, u=U_S, v=V_S, s=S_S)
! Singular values that are larger than epsilon determine
! the rank=k.
k = count(S_S > epsilon(one))
oldrms = huge(one)
g = matmul(transpose(U_S), b(1:m,1))
! Find the minimum number of singular values that gives a good
! approximation to f(t) = 1.
do i=1,k
f(1:n,1) = matmul(V_S(1:,1:i), g(1:i)/S_S(1:i))
f = f - one
rms = sum(f**2)/n
if (rms > oldrms) exit
oldrms = rms
end do
write (*,"( ' Using this number of singular values, ', &
&i4 / ' the approximate R.M.S. error is ', 1pe12.4)") &
i-1, oldrms
if (sqrt(oldrms) <= delta_t**2) then
write (*,*) 'Example 4 for LIN_SOL_SVD is correct.'
end if
end
Output
Example 4 for LIN_SOL_SVD is correct.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |