Computes the singular value decomposition (SVD) of a
rectangular matrix, A. This gives the
decomposition
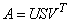
where V is an n × n orthogonal matrix, U is an m × m orthogonal matrix, and S is a real, rectangular diagonal matrix.
Required Arguments
A — Array of size m ×
n containing the matrix. (Input [/Output])
If the packaged option
lin_svd_overwrite_input
is used, this array is not saved on output.
S — Array of size min(m, n) containing the real singular values. These nonnegative values are in non-increasing order. (Output)
U — Array of size m × m containing the singular vectors, U. (Output)
V — Array of size n × n containing the singular vectors, V. (Output)
Optional Arguments
MROWS = m
(Input)
Uses array A(1:m, 1:n) for the input
matrix.
Default: m = size(A, 1)
NCOLS = n
(Input)
Uses array A(1:m, 1:n) for the input
matrix.
Default: n = size(A, 2)
RANK = k
(Output)
Number of singular values that exceed the value Small. RANK will satisfy
k <= min(m, n).
iopt =
iopt(:) (Input)
Derived type array with the same precision
as the input matrix. Used for passing optional data to the routine. The options
are as follows:
|
Packaged Options for LIN_SVD | ||
|
Option Prefix = ? |
Option Name |
Option Value |
|
S_, d_, c_, z_ |
lin_svd_set_small |
1 |
|
S_, d_, c_, z_ |
lin_svd_overwrite_input |
2 |
|
S_, d_, c_, z_ |
lin_svd_scan_for_NaN |
3 |
|
S_, d_, c_, z_ |
lin_svd_use_qr |
4 |
|
S_, d_, c_, z_ |
lin_svd_skip_orth |
5 |
|
S_, d_, c_, z_ |
lin_svd_use_gauss_elim |
6 |
|
S_, d_, c_, z_ |
lin_svd_set_perf_ratio |
7 |
iopt(IO) =
?_options(?_lin_svd_set_small, Small)
If a singular
value is smaller than Small, it is defined as zero for the purpose of
computing the rank of A.
Default: the smallest number that can be
reciprocated safely
iopt(IO) =
?_options(?_lin_svd_overwrite_input, ?_dummy)
Does not save the input
array A(:, :).
iopt(IO) =
?_options(?_lin_svd_scan_for_NaN, ?_dummy)
Examines each input array
entry to find the first value such that
isNaN(a(i,j)) == .true.
See the isNaN() function,
Chapter 10.
Default:
The array is not scanned for NaNs.
iopt(IO) =
?_options(?_lin_svd_use_qr, ?_dummy)
Uses a rational QR
algorithm to compute eigenvalues. Accumulate the singular vectors using this
algorithm.
Default: singular vectors computed using inverse iteration
iopt(IO) =
?_options(?_lin_svd_skip_Orth, ?_dummy)
If the eigenvalues are
computed using inverse iteration, skips the final orthogonalization of the
vectors. This method results in a more efficient computation. However, the
singular vectors, while a complete set, may not be orthogonal.
Default:
singular vectors are orthogonalized if obtained using inverse iteration
iopt(IO) =
?_options(?_lin_svd_use_gauss_elim, ?_dummy)
If the eigenvalues are
computed using inverse iteration, uses standard elimination with partial
pivoting to solve the inverse iteration problems.
Default: singular vectors
computed using cyclic reduction
iopt(IO) =
?_options(?_lin_svd_set_perf_ratio, perf_ratio)
Uses residuals
for approximate normalized singular vectors if they have a performance index no
larger than perf_ratio. Otherwise an alternate approach is taken and the
singular vectors are computed again: Standard elimination is used instead of
cyclic reduction, or the standard QR algorithm is used as a backup
procedure to inverse iteration. Larger values of perf_ratio are less
likely to cause these exceptions.
Default: perf_ratio = 4
FORTRAN 90 Interface
Generic: CALL LIN_SVD (A, S, U, V [,…])
Specific: The specific interface names are S_LIN_SVD, D_LIN_SVD, C_LIN_SVD, and Z_LIN_SVD.
Description
Routine lin_svd is an implementation of the QR algorithm for computing the SVD of rectangular matrices. An orthogonal reduction of the input matrix to upper bidiagonal form is performed. Then, the SVD of a real bidiagonal matrix is calculated. The orthogonal decomposition AV = US results from products of intermediate matrix factors. See Golub and Van Loan (1989, Chapter 8) for details.
Fatal, Terminal, and Warning Error Messages
See the messages.gls file for error messages for LIN_SVD. These error messages are numbered 1001-1010; 1021-1030; 1041-1050; 1061-1070.
.p>.F90CH2.DOC!EX1_LIN_SVD;Example 1: Computing the SVD
The SVD of a square, random matrix A is computed. The residuals R = AV - US are small with respect to working precision. Also, see operator_ex21, supplied with the product examples.
use lin_svd_int
use rand_gen_int
implicit none
! This is Example 1 for LIN_SVD.
integer, parameter :: n=32
real(kind(1d0)), parameter :: one=1d0
real(kind(1d0)) err
real(kind(1d0)), dimension(n,n) :: A, U, V, S(n), y(n*n)
! Generate a random n by n matrix.
call rand_gen(y)
A = reshape(y,(/n,n/))
! Compute the singular value decomposition.
call lin_svd(A, S, U, V)
! Check for small residuals of the expression A*V - U*S.
err = sum(abs(matmul(A,V) - U*spread(S,dim=1,ncopies=n))) &
/ sum(abs(S))
if (err <= sqrt(epsilon(one))) then
write (*,*) 'Example 1 for LIN_SVD is correct.'
end if
end
Output
Example 1 for LIN_SVD is correct.
Additional Examples
.p>.F90CH2.DOC!EX2_LIN_SVD;Example 2: Linear Least Squares with a Quadratic Constraint
An m × n matrix equation Ax ≅ b, m > n, is approximated in a least-squares sense. The matrix b is size m × k. Each of the k solution vectors of the matrix x is constrained to have Euclidean length of value αj > 0. The value of αi is chosen so that the constrained solution is 0.25 the length of the nonregularized or standard least-squares equation. See Golub and Van Loan (1989, Chapter 12) for more details. In the Example 2 code, Newton's method is used to solve for each regularizing parameter of the k systems. The solution is then computed and its length is checked. Also, see operator_ex22, supplied with the product examples.
use lin_svd_int
use rand_gen_int
implicit none
! This is Example 2 for LIN_SVD.
integer, parameter :: m=64, n=32, k=4
real(kind(1d0)), parameter :: one=1d0, zero=0d0
real(kind(1d0)) a(m,n), s(n), u(m,m), v(n,n), y(m*max(n,k)), &
b(m,k), x(n,k), g(m,k), alpha(k), lamda(k), &
delta_lamda(k), t_g(n,k), s_sq(n), phi(n,k), &
phi_dot(n,k), rand(k), err
! Generate a random matrix for both A and B.
call rand_gen(y)
a = reshape(y,(/m,n/))
call rand_gen(y)
b = reshape(y,(/m,k/))
! Compute the singular value decomposition.
call lin_svd(a, s, u, v)
! Choose alpha so that the lengths of the regularized solutions
! are 0.25 times lengths of the non-regularized solutions.
g = matmul(transpose(u),b)
x = matmul(v,spread(one/s,dim=2,ncopies=k)*g(1:n,1:k))
alpha = 0.25*sqrt(sum(x**2,dim=1))
t_g = g(1:n,1:k)*spread(s,dim=2,ncopies=k)
s_sq = s**2; lamda = zero
solve_for_lamda: do
x=one/(spread(s_sq,dim=2,ncopies=k)+ &
spread(lamda,dim=1,ncopies=n))
phi = (t_g*x)**2; phi_dot = -2*phi*x
delta_lamda = (sum(phi,dim=1)-alpha**2)/sum(phi_dot,dim=1)
! Make Newton method correction to solve the secular equations for
! lamda.
lamda = lamda - delta_lamda
if (sum(abs(delta_lamda)) <= &
sqrt(epsilon(one))*sum(lamda)) &
exit solve_for_lamda
! This is intended to fix up negative solution approximations.
call rand_gen(rand)
where (lamda < 0) lamda = s(1) * rand
end do solve_for_lamda
! Compute solutions and check lengths.
x = matmul(v,t_g/(spread(s_sq,dim=2,ncopies=k)+ &
spread(lamda,dim=1,ncopies=n)))
err = sum(abs(sum(x**2,dim=1) - alpha**2))/sum(abs(alpha**2))
if (err <= sqrt(epsilon(one))) then
write (*,*) 'Example 2 for LIN_SVD is correct.'
end if
end
Output
Example 2 for LIN_SVD is correct.
.p>.F90CH2.DOC!EX3_LIN_SVD;Example 3: Generalized Singular Value Decomposition
The n × n matrices A and B are expanded in a Generalized Singular Value Decomposition (GSVD). Two n × n orthogonal matrices, U and V, and a nonsingular matrix X are computed such that
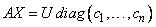
and
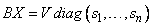
The values 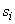 and
and 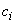 are normalized so that
are normalized so that
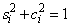
The 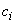 are nonincreasing, and the
are nonincreasing, and the 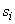 are nondecreasing. See Golub
and Van Loan (1989, Chapter 8) for more details. Our method is based on
computing three SVDs as opposed to the QR decomposition and two SVDs
outlined in Golub and Van Loan. As a bonus, an SVD of the matrix X is
obtained, and you can use this information to answer further questions about its
conditioning. This form of the decomposition assumes that the matrix
are nondecreasing. See Golub
and Van Loan (1989, Chapter 8) for more details. Our method is based on
computing three SVDs as opposed to the QR decomposition and two SVDs
outlined in Golub and Van Loan. As a bonus, an SVD of the matrix X is
obtained, and you can use this information to answer further questions about its
conditioning. This form of the decomposition assumes that the matrix
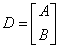
has all its singular values strictly positive. For alternate problems, where some singular values of D are zero, the GSVD becomes
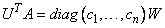
and
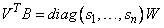
The matrix W has the same singular values as the matrix D. Also, see operator_ex23, supplied with the product examples.
use lin_svd_int
use rand_gen_int
implicit none
! This is Example 3 for LIN_SVD.
integer, parameter :: n=32
integer i
real(kind(1d0)), parameter :: one=1.0d0
real(kind(1d0)) a(n,n), b(n,n), d(2*n,n), x(n,n), u_d(2*n,2*n), &
v_d(n,n), v_c(n,n), u_c(n,n), v_s(n,n), u_s(n,n), &
y(n*n), s_d(n), c(n), s(n), sc_c(n), sc_s(n), &
err1, err2
! Generate random square matrices for both A and B.
call rand_gen(y)
a = reshape(y,(/n,n/))
call rand_gen(y)
b = reshape(y,(/n,n/))
! Construct D; A is on the top; B is on the bottom.
d(1:n,1:n) = a
d(n+1:2*n,1:n) = b
! Compute the singular value decompositions used for the GSVD.
call lin_svd(d, s_d, u_d, v_d)
call lin_svd(u_d(1:n,1:n), c, u_c, v_c)
call lin_svd(u_d(n+1:,1:n), s, u_s, v_s)
! Rearrange c(:) so it is non-increasing. Move singular
! vectors accordingly. (The use of temporary objects sc_c and
! x is required.)
sc_c = c(n:1:-1); c = sc_c
x = u_c(1:n,n:1:-1); u_c = x
x = v_c(1:n,n:1:-1); v_c = x
! The columns of v_c and v_s have the same span. They are
! equivalent by taking the signs of the largest magnitude values
! positive.
do i=1, n
sc_c(i) = sign(one,v_c(sum(maxloc(abs(v_c(1:n,i)))),i))
sc_s(i) = sign(one,v_s(sum(maxloc(abs(v_s(1:n,i)))),i))
end do
v_c = v_c*spread(sc_c,dim=1,ncopies=n)
u_c = u_c*spread(sc_c,dim=1,ncopies=n)
v_s = v_s*spread(sc_s,dim=1,ncopies=n)
u_s = u_s*spread(sc_s,dim=1,ncopies=n)
! In this form of the GSVD, the matrix X can be unstable if D
! is ill-conditioned.
x = matmul(v_d*spread(one/s_d,dim=1,ncopies=n),v_c)
! Check residuals for GSVD, A*X = u_c*diag(c_1, ..., c_n), and
! B*X = u_s*diag(s_1, ..., s_n).
err1 = sum(abs(matmul(a,x) - u_c*spread(c,dim=1,ncopies=n))) &
/ sum(s_d)
err2 = sum(abs(matmul(b,x) - u_s*spread(s,dim=1,ncopies=n))) &
/ sum(s_d)
if (err1 <= sqrt(epsilon(one)) .and. &
err2 <= sqrt(epsilon(one))) then
write (*,*) 'Example 3 for LIN_SVD is correct.'
end if
end
.p>.F90CH2.DOC!EX4_LIN_SVD;Example 4: Ridge Regression as Cross-Validation with Weighting
This example illustrates a particular choice for the ridge regression problem: The least-squares problem Ax ≅ b is modified by the addition of a regularizing term to become
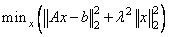
The solution to this problem, with row k deleted, is denoted by xk(l). Using nonnegative weights (w1, …, wm), the cross-validation squared error C(l) is given by:
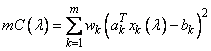
With the SVD A = USVT and product g = UTb, this quantity can be written as

This expression is minimized.
See Golub and Van Loan (1989, Chapter 12) for more details. In the Example 4
code, mC(l), at p = 10
grid points are evaluated using a log-scale with respect to l, 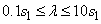 . Array operations and intrinsics are used to evaluate the
function and then to choose an approximate minimum. Following the computation of
the optimum l, the regularized
solutions are computed. Also, see
operator_ex24,
supplied with the product examples.
. Array operations and intrinsics are used to evaluate the
function and then to choose an approximate minimum. Following the computation of
the optimum l, the regularized
solutions are computed. Also, see
operator_ex24,
supplied with the product examples.
use lin_svd_int
use rand_gen_int
implicit none
! This is Example 4 for LIN_SVD.
integer i
integer, parameter :: m=32, n=16, p=10, k=4
real(kind(1d0)), parameter :: one=1d0
real(kind(1d0)) log_lamda, log_lamda_t, delta_log_lamda
real(kind(1d0)) a(m,n), b(m,k), w(m,k), g(m,k), t(n), s(n), &
s_sq(n), u(m,m), v(n,n), y(m*max(n,k)), &
c_lamda(p,k), lamda(k), x(n,k), res(n,k)
! Generate random rectangular matrices for A and right-hand
! sides, b.
call rand_gen(y)
a = reshape(y,(/m,n/))
call rand_gen(y)
b = reshape(y,(/m,k/))
! Generate random weights for each of the right-hand sides.
call rand_gen(y)
w = reshape(y,(/m,k/))
! Compute the singular value decomposition.
call lin_svd(a, s, u, v)
g = matmul(transpose(u),b)
s_sq = s**2
log_lamda = log(10.*s(1)); log_lamda_t=log_lamda
delta_log_lamda = (log_lamda - log(0.1*s(n))) / (p-1)
! Choose lamda to minimize the "cross-validation" weighted
! square error. First evaluate the error at a grid of points,
! uniform in log_scale.
cross_validation_error: do i=1, p
t = s_sq/(s_sq+exp(log_lamda))
c_lamda(i,:) = sum(w*((b-matmul(u(1:m,1:n),g(1:n,1:k)* &
spread(t,DIM=2,NCOPIES=k)))/ &
(one-matmul(u(1:m,1:n)**2, &
spread(t,DIM=2,NCOPIES=k))))**2,DIM=1)
log_lamda = log_lamda - delta_log_lamda
end do cross_validation_error
! Compute the grid value and lamda corresponding to the minimum.
do i=1, k
lamda(i) = exp(log_lamda_t - delta_log_lamda* &
(sum(minloc(c_lamda(1:p,i)))-1))
end do
! Compute the solution using the optimum "cross-validation"
! parameter.
x = matmul(v,g(1:n,1:k)*spread(s,DIM=2,NCOPIES=k)/ &
(spread(s_sq,DIM=2,NCOPIES=k)+ &
spread(lamda,DIM=1,NCOPIES=n)))
! Check the residuals, using normal equations.
res = matmul(transpose(a),b-matmul(a,x)) - &
spread(lamda,DIM=1,NCOPIES=n)*x
if (sum(abs(res))/sum(s_sq) <= &
sqrt(epsilon(one))) then
write (*,*) 'Example 4 for LIN_SVD is correct.'
end if
end
Output
Example 4 for LIN_SVD is correct.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |