Computes an updated QR factorization after the rank-one matrix axyT is added.
Required Arguments
ALPHA — Scalar determining the rank-one update to be added. (Input)
W — Vector of length NROW determining the
rank-one matrix to be added. (Input)
The updated matrix is
A + axyT. If I = 0 then W
contains the vector x. If I = 1 then W
contains the vector QTx.
Y — Vector of length NCOL determining the rank-one matrix to be added. (Input)
R — Matrix of order NROW by NCOL containing the
R matrix from the QR factorization. (Input)
Only
the upper trapezoidal part of R is referenced.
IPATH — Flag used to control the computation
of the QR update. (Input)
IPATH has the decimal
expansion IJ
such that: I = 0
means W contains the vector x.
I= 1 means W contains the vector
QTx.
J = 0 means do not update
the matrix Q.
J = 1 means
update the matrix Q. For example, if IPATH = 10 then, I = 1 and J = 0.
RNEW — Matrix of order NROW by NCOL containing the
updated R matrix
in the QR factorization. (Output)
Only the upper
trapezoidal part of RNEW is updated. R and RNEW may be the
same.
Optional Arguments
NROW — Number of rows in the matrix A =
Q *
R. (Input)
Default: NROW = size (W,1).
NCOL — Number of columns in the matrix
A = Q *
R. (Input)
Default: NCOL = size (Y,1).
Q — Matrix of order NROW containing the
Q matrix from the QR factorization. (Input)
Ignored if IPATH = 0.
Default:
Q is 1x1 and
un-initialized.
LDQ — Leading dimension of Q exactly as specified
in the dimension statement of the calling program. (Input)
Ignored if IPATH = 0.
Default:
LDQ = size
(Q,1).
LDR — Leading dimension of R exactly as specified
in the dimension statement of the calling program.
(Input)
Default: LDR = size (R,1).
QNEW — Matrix of order NROW containing the
updated Q matrix
in the QR factorization. (Output)
Ignored if J = 0, see IPATH for definition
of J.
LDQNEW — Leading dimension of QNEW exactly as
specified in the dimension statement of the calling program. (Input)
Ignored if J
= 0; see IPATH
for definition of J.
Default: LDQNEW = size
(QNEW,1).
LDRNEW — Leading dimension of RNEW exactly as
specified in the dimension statement of the calling program.
(Input)
Default: LDRNEW = size (RNEW,1).
FORTRAN 90 Interface
Generic: CALL LUPQR (ALPHA, W, Y, R, IPATH, RNEW [,…])
Specific: The specific interface names are S_LUPQR and D_LUPQR.
FORTRAN 77 Interface
Single: CALL LUPQR (NROW, NCOL, ALPHA, W, Y, Q, LDQ, R, LDR, IPATH, QNEW, LDQNEW, RNEW, LDRNEW)
Double: The double precision name is DLUPQR.
Description
Let A be an m × n matrix and let A = QR be its QR decomposition. (In the program, m is called NROW and n is called NCOL) Then
A + αxyT = QR + αxyT = Q(R + αQTxyT) = Q(R + αwyT)
where w = QT x. An orthogonal transformation J can be constructed, using a sequence of m − 1 Givens rotations, such that Jw = ωe1, where ω = ±||w||2 and e1 = (1, 0, …, 0)T. Then
A + αxyT = (QJT )(JR + αωe1yT)
Since JR is an upper Hessenberg matrix, H = JR + αωe1yT is also an upper Hessenberg matrix. Again using m − 1 Givens rotations, an orthogonal transformation G can be constructed such that GH is an upper triangular matrix. Then
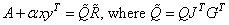
is orthogonal and
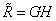
is upper triangular.
If the last k components of w are zero, then
the number of Givens rotations needed to construct
J or G is
m − k
− 1 instead of m
− 1.
For further information, see Dennis and Schnabel (1983, pages 55− 58 and 311−313), or Golub and Van Loan (1983, pages 437− 439).
Comments
1. Workspace may be explicitly provided, if desired, by use of L2PQR/DL2PQR. The reference is:
CALL L2PQR (NROW, NCOL, ALPHA, W, Y, Q, LDQ, R, LDR, IPATH, QNEW, LDQNEW, RNEW, LDRNEW, Z, WORK)
The additional arguments are as follows:
Z — Work vector of length NROW.
WORK — Work vector of length MIN(NROW − 1, NCOL).
Example
The QR factorization of A is found. It is then used to find the QR factorization of A + xyT. Since pivoting is used, the QR factorization routine finds AP = QR, where P is a permutation matrix determined by IPVT. We compute
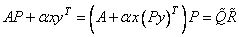
The IMSL routine PERMU (see Utilities) is used to compute Py. As a check
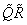
is computed and printed. It can also be obtained from A + xyT by permuting its columns using the order given by IPVT.
USE
IMSL_LIBRARIES
!
Declare variables
INTEGER LDA, LDAQR, LDQ, LDQNEW, LDQR, LDR, LDRNEW, NCOL, NROW
PARAMETER (NCOL=3, NROW=4, LDA=NROW, LDAQR=NROW, LDQ=NROW, &
LDQNEW=NROW, LDQR=NROW, LDR=NROW, LDRNEW=NROW)
!
INTEGER IPATH, IPVT(NCOL), J, MIN0
REAL A(LDA,NCOL), ALPHA, AQR(LDAQR,NCOL), CONORM(NCOL), &
Q(LDQ,NROW), QNEW(LDQNEW,NROW), QR(LDQR,NCOL), &
QRAUX(NCOL), R(LDR,NCOL), RNEW(LDRNEW,NCOL), W(NROW), &
Y(NCOL)
LOGICAL PIVOT
INTRINSIC MIN0
!
! Set values for A
!
! A = ( 1 2 4 )
! ( 1 4 16 )
! ( 1 6 36 )
! ( 1 8 64 )
!
DATA A/4*1.0, 2.0, 4.0, 6.0, 8.0, 4.0, 16.0, 36.0, 64.0/
! Set values for W and Y
DATA W/1., 2., 3., 4./
DATA Y/3., 2., 1./
!
! QR factorization
! Set IPVT = 0 (all columns free)
IPVT = 0
PIVOT = .TRUE.
CALL LQRRR (A, QR, QRAUX, IPVT=IPVT, PIVOT=PIVOT)
! Accumulate Q
CALL LQERR (QR, QRAUX, Q)
! Permute Y
CALL PERMU (Y, IPVT, Y)
! R is the upper trapezoidal part of QR
R = 0.0E0
DO 10 J=1, NCOL
CALL SCOPY (MIN0(J,NROW), QR(:,J), 1, R(:,J), 1)
10 CONTINUE
! Update Q and R
ALPHA =
1.0
IPATH = 01
CALL LUPQR (ALPHA, W, Y, R, IPATH, RNEW, Q=Q, QNEW=QNEW)
! Compute AQR = Q*R
CALL MRRRR (QNEW, RNEW, AQR)
! Print results
CALL WRIRN ('IPVT', IPVT, 1, NCOL,1)
CALL WRRRN ('QNEW', QNEW)
CALL WRRRN ('RNEW', RNEW)
CALL WRRRN ('QNEW*RNEW', AQR)
END
Output
IPVT
1 2
3
3 2
1
QNEW
1 2 3 4
1 -0.0620 -0.5412 0.8082 -0.2236
2 -0.2234 -0.6539 -0.2694 0.6708
3 -0.4840 -0.3379 -0.4490 -0.6708
4 -0.8438 0.4067 0.2694 0.2236
RNEW
1 2 3
1 -80.59 -21.34 -17.62
2 0.00 -4.94 -4.83
3 0.00 0.00 0.36
4 0.00 0.00 0.00
QNEW*RNEW
1 2 3
1 5.00 4.00 4.00
2 18.00 8.00 7.00
3 39.00 12.00 10.00
4 68.00 16.00 13.00
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |