
Computes the coordinate transformation, projection, and complete the solution of the least-squares problem Ax = b.
Required Arguments
KBASIS Number of columns of the submatrix
Ak
of A. (Input)
The value KBASIS must not exceed
min(NRA, NCA), where NCA is the number of
columns in matrix A. The value NCA is an argument to
routine LQRRR. The value of KBASIS is normally
NCA unless the
matrix is rank-deficient. The user must analyze the problem data and determine
the value of KBASIS. See Comments.
QR NRA by NCA array containing information about the QR factorization of A as output from routine LQRRR/DLQRRR. (Input)
QRAUX Vector of length NCA containing information about the QR factorization of A as output from routine LQRRR/DLQRRR. (Input)
B Vector b of length NRA to be manipulated. (Input)
IPATH Option parameter specifying what is to
be computed. (Input)
The value IPATH has the decimal
expansion IJKLM,
such that:
I
≠ 0 means compute
Qb;
J
≠ 0 means compute
QTb;
K ≠ 0 means compute QTb and
x;
L
≠ 0 means compute QTb and b
−
Ax;
M
≠ 0 means compute
QTb and Ax.
For example, if the decimal number IPATH = 01101, then
I = 0, J = 1, K = 1,
L= 0, and M= 1.
Optional Arguments
NRA Number of rows of matrix
A. (Input)
Default: NRA = size (QR,1).
LDQR Leading dimension of QR exactly
as specified in the dimension statement of the calling program.
(Input)
Default: LDQR = size (QR,1).
QB Vector of length NRA containing Qb if requested in the option IPATH. (Output)
QTB Vector of length NRA containing QTb if requested in the option IPATH. (Output)
X Vector of length KBASIS containing the
solution of the least-squares problem Akx = b, if this is requested
in the option IPATH.
(Output)
If pivoting was requested in routine LQRRR/DLQRRR, then the J-th entry of X will be associated
with column IPVT(J) of the original
matrix A. See Comments.
RES Vector of length NRA containing the
residuals (b − Ax) of the least-squares problem if requested in
the option IPATH.
(Output)
This vector is the orthogonal projection of b
onto the orthogonal complement of the column space of A.
AX Vector of length NRA containing the
least-squares approximation Ax if requested in the option IPATH.
(Output)
This vector is the orthogonal projection of b onto the
column space of A.
FORTRAN 90 Interface
Generic: CALL LQRSL (KBASIS, QR, QRAUX, B, IPATH [, ])
Specific: The specific interface names are S_LQRSL and D_LQRSL.
FORTRAN 77 Interface
Single: CALL LQRSL (NRA, KBASIS, QR, LDQR, QRAUX, B, IPATH, QB, QTB, X, RES, AX)
Double: The double precision name is DLQRSL.
ScaLAPACK Interface
Generic: CALL LQRSL (KBASIS, QR0, QRAUX0, B0, IPATH [, ])
Specific: The specific interface names are S_LQRSL and D_LQRSL.
See the ScaLAPACK Usage Notes below for a description of the arguments for distributed computing.
Description
The underlying code of routine LQRSL is based on either LINPACK , LAPACK, or ScaLAPACK code depending upon which supporting libraries are used during linking. For a detailed explanation see Using ScaLAPACK, LAPACK, LINPACK, and EISPACK in the Introduction section of this manual.
The most important use of LQRSL is for solving the least-squares problem Ax = b, with coefficient matrix A and data vector b. This problem can be formulated, using the normal equations method, as AT Ax = AT b. Using LQRRR the QR decomposition of A, AP = QR, is computed. Here P is a permutation matrix (P = P), Q is an orthogonal matrix (Q = QT) and R is an upper trapezoidal matrix. The normal equations can then be written as
(PRT)(QTQ)R(PTx) = (PRT)QT b
If ATA is
nonsingular, then R is also nonsingular and the normal equations can be
written as
R(PTx) =
QT b. LQRSL
can be used to compute QT b and then
solve for PT x. Note that
the permuted solution is returned.
The routine LQRSL can also be used to compute the least-squares residual, b − Ax. This is the projection of b onto the orthogonal complement of the column space of A. It can also compute Qb, QTb and Ax, the orthogonal projection of x onto the column space of A.
Comments
1. Informational error
Type Code
4 1 Computation of the least-squares solution of AK * X = B is requested, but the upper triangular matrix R from the QR factorization is singular.
2. This routine is designed to be used together with LQRRR. It assumes that LQRRR/DLQRR has been called to get QR, QRAUX and IPVT. The submatrix Ak mentioned above is actually equal to Ak = (A(IPVT(1)), A(IPVT(2)), , A(IPVT (KBASIS))), where A(IPVT(I)) is the IPVT(I)-th column of the original matrix.
ScaLAPACK Usage Notes
The arguments which differ from the standard version of this routine are:
QR0 MXLDA by MXCOL local matrix containing the local portions of the distributed matrix QR. QR contains the factored form of the matrix Q in the first min(NRQR, NCQR) columns of the strict lower trapezoidal part of QR as output from subroutine LQRRR/DLQRRR. (Input)
QRAUX0 Real vector of length MXCOL containing the local portions of the distributed matrix QRAUX. QRAUX contains the information about the orthogonal part of the decomposition in the first min(NRA, NCA) positions as output from subroutine LQRRR/DLQRRR. (Input)
B0 Real vector of length MXLDA containing the local portions of the distributed vector B. B contains the vector to be manipulated. (Input)
QB0 Real vector of length MXLDA containing the local portions of the distributed vector Qb if requested in the option IPATH. (Output)
QTB0 Real vector of length MXLDA containing the local portions of the distributed vector QTb if requested in the option IPATH. (Output)
X0 Real vector of length MXLDX containing the
local portions of the distributed vector X. X contains the
solution of the least-squares problem Akx = b, if this is requested
in the option IPATH.
(Output)
If pivoting was requested in routine LQRRR/DLQRRR, then the J-th entry of X will be associated
with column IPVT(J) of the original
matrix A. See Comments.
RES0 Real vector of length MXLDA containing the
local portions of the distributed vector RES. RES contains the
residuals (b − Ax) of the least-squares problem if requested in
the option IPATH.
(Output)
This vector is the orthogonal projection of b onto the
orthogonal complement of the column space of A.
AX0 Real vector of length MXLDA containing the
local portions of the distributed vector AX. AX contains the
least-squares approximation Ax if requested in the option IPATH.
(Output)
This vector is the orthogonal projection of b onto the
column space of A.
All other arguments are global and are the same as described for the standard version of the routine. In the argument descriptions above, MXLDA, MXLDX and MXCOL can be obtained through a call to SCALAPACK_GETDIM (see Utilities) after a call to SCALAPACK_SETUP (see Utilities) has been made. See the ScaLAPACK Example below.
Example
Consider the problem of finding the coefficients ci in
f(x) = c0 + c1x + c2x2
given data at xi = 2i,i = 1, 2, 3, 4, using the method of least squares. The row of the matrix A contains the value of 1, xi and
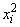
at the data points. The vector b contains the data. The routine LQRRR is used to compute the QR decomposition of A. Then LQRSL is then used to solve the least-squares problem and compute the residual vector.
USE IMSL_LIBRARIES
! Declare variables
PARAMETER (NRA=4, NCA=3, KBASIS=3, LDA=NRA, LDQR=NRA)
INTEGER IPVT(NCA)
REAL A(LDA,NCA), QR(LDQR,NCA), QRAUX(NCA), CONORM(NCA), &
X(KBASIS), QB(1), QTB(NRA), RES(NRA), &
AX(1), B(NRA)
LOGICAL PIVOT
!
! Set values for A
!
! A = ( 1 2 4 )
! ( 1 4 16 )
! ( 1 6 36 )
! ( 1 8 64 )
!
DATA A/4*1.0, 2.0, 4.0, 6.0, 8.0, 4.0, 16.0, 36.0, 64.0/
!
! Set values for B
!
! B = ( 16.99 57.01 120.99 209.01 )
DATA B/ 16.99, 57.01, 120.99, 209.01 /
!
! QR factorization
PIVOT = .TRUE.
IPVT = 0
CALL LQRRR (A, QR, QRAUX, PIVOT=PIVOT, IPVT=IPVT)
! Solve the least squares problem
IPATH = 00110
CALL LQRSL (KBASIS, QR, QRAUX, B, IPATH, X=X, RES=RES)
! Print results
CALL WRIRN ('IPVT', IPVT, 1, NCA, 1)
CALL WRRRN ('X', X, 1, KBASIS, 1)
CALL WRRRN ('RES', RES, 1, NRA, 1)
!
END
Output
IPVT
1 2
3
3 2 1
X
1 2 3
3.000 2.002 0.990
RES
1 2 3 4
-0.00400 0.01200 -0.01200 0.00400
Note that since
IPVT is (3,
2, 1) the array X contains the solution
coefficients ci in reverse
order.
ScaLAPACK Example
The previous example is repeated here as a distributed example. Consider the problem of finding the coefficients ci in
f(x) = c0 + c1x + c2x2
given data at xi = 2i, i = 1, 2, 3, 4, using the method of least squares. The row of the matrix A contains the value of 1, xi and
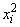
at the data points. The vector b contains the data.
The routine LQRRR
is used to compute the QR decomposition of A. Then LQRSL
is then used to solve the least-squares problem and compute the residual vector.
SCALAPACK_MAP
and SCALAPACK_UNMAP
are IMSL utility routines
(see Utilities) used
to map and unmap arrays to and from the processor grid. They are used here for
brevity. DESCINIT
is a ScaLAPACK tools routine which initializes the descriptors for the local
arrays.
USE
MPI_SETUP_INT
USE
LQRRR_INT
USE
LQRSL_INT
USE
WRIRN_INT
USE
WRRRN_INT
USE
SCALAPACK_SUPPORT
IMPLICIT
NONE
INCLUDE mpif.h'
! Declare variables
INTEGER KBASIS, LDA, LDQR, NCA, NRA,
DESCA(9), DESCL(9),
&
DESCX(9), DESCB(9)
INTEGER INFO, MXCOL, MXCOLX, MXLDA, MXLDX,
LDQ, IPATH
INTEGER, ALLOCATABLE
:: IPVT(:), IPVT0(:)
REAL, ALLOCATABLE :: A(:,:), B(:),
QR(:,:), QRAUX(:), X(:),
&
RES(:)
REAL, ALLOCATABLE :: A0(:,:),
QR0(:,:), QRAUX0(:), X0(:),
&
RES0(:), B0(:), QTB0(:)
LOGICAL PIVOT
PARAMETER (NRA=4, NCA=3, LDA=NRA, LDQR=NRA, KBASIS=3)
! Set up for MPI
MP_NPROCS =
MP_SETUP()
IF(MP_RANK .EQ. 0)
THEN
ALLOCATE
(A(LDA,NCA), B(NRA), QR(LDQR,NCA),
&
QRAUX(NCA),
IPVT(NCA), X(NCA), RES(NRA))
! Set values for A and the righthand sides
A(1,:)
= (/ 1.0, 2.0,
4.0/)
A(2,:) = (/
1.0, 4.0,
16.0/)
A(3,:) = (/
1.0, 6.0,
36.0/)
A(4,:) = (/
1.0, 8.0, 64.0/)
!
B = (/ 16.99, 57.01, 120.99, 209.01 /)
!
IPVT =
0
ENDIF
! Set up a 1D processor grid and define
! its context ID, MP_ICTXT
CALL SCALAPACK_SETUP(NRA, NCA, .TRUE., .TRUE.)
! Get the array descriptor entities MXLDA,
! and MXCOL
CALL SCALAPACK_GETDIM(NRA, NCA, MP_MB, MP_NB, MXLDA, MXCOL)
CALL SCALAPACK_GETDIM(KBASIS, 1, MP_NB, 1, MXLDX, MXCOLX)
! Set up the array descriptors
CALL DESCINIT(DESCA, NRA, NCA, MP_MB, MP_NB, 0, 0, MP_ICTXT, & MXLDA,INFO)
CALL DESCINIT(DESCL, 1, NCA, 1, MP_NB, 0, 0, MP_ICTXT, 1, INFO)
CALL DESCINIT(DESCX, KBASIS, 1,
MP_NB, 1, 0, 0, MP_ICTXT, MXLDX, INFO)
CALL
DESCINIT(DESCB, NRA, 1, MP_MB, 1, 0, 0, MP_ICTXT, MXLDA, INFO)
! Allocate space for the local arrays
ALLOCATE (A0(MXLDA,MXCOL), QR0(MXLDA,MXCOL), QRAUX0(MXCOL), & IPVT0(MXCOL), B0(MXLDA), X0(MXLDX), RES0(MXLDA), QTB0(MXLDA))
! Map input array to the processor grid
CALL SCALAPACK_MAP(A, DESCA, A0)
CALL SCALAPACK_MAP(B, DESCB,
B0)
PIVOT = .TRUE.
CALL SCALAPACK_MAP(IPVT, DESCL, IPVT0)
! QR factorization
CALL LQRRR (A0, QR0, QRAUX0, PIVOT=PIVOT, IPVT=IPVT0)
IPATH = 00110
CALL LQRSL (KBASIS, QR0, QRAUX0, B0, IPATH, QTB=QTB0, X=X0, RES=RES0)
! Unmap the results from the distributed
! array back to a non-distributed array.
! After the unmap, only Rank=0 has the full
! array.
CALL SCALAPACK_UNMAP(IPVT0, DESCL, IPVT, NCA, .FALSE.)
CALL SCALAPACK_UNMAP(X0, DESCX, X)
CALL SCALAPACK_UNMAP(RES0, DESCB, RES)
! Print results.
! Only Rank=0 has the solution, X.
IF(MP_RANK .EQ. 0) THEN
CALL WRIRN ('IPVT', IPVT, 1, NCA, 1)
CALL WRRRN ('X', X, 1, KBASIS, 1)
CALL WRRRN ('RES', RES, 1, NRA, 1)
ENDIF
! Exit ScaLAPACK usage
CALL SCALAPACK_EXIT(MP_ICTXT)
! Shut down MPI
MP_NPROCS =
MP_SETUP(FINAL')
END
Output
IPVT
1 2
3
3 2 1
X
1 2 3
3.000 2.002 0.990
RES
1 2 3 4
-0.00400 0.01200 -0.01200 0.00400
Note that since
IPVT is (3,
2, 1) the array X contains the solution
coefficients ci in reverse
order.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |