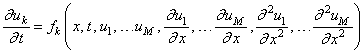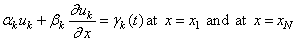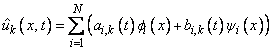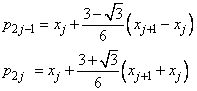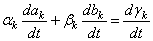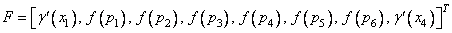Solves a system of partial differential equations of the form ut = f(x, t, u, ux, uxx) using the method of lines. The solution is represented with cubic Hermite polynomials.
Required Arguments
IDO Flag indicating the state of the computation. (Input/Output)
IDO State
1 Initial entry
2 Normal reentry
3 Final call, release workspace
Normally, the initial call is made with IDO = 1. The routine then sets IDO = 2, and this value is then used for all but the last call that is made with IDO = 3.
FCNUT
User-supplied SUBROUTINE to evaluate
the function ut. The usage is
CALL FCNUT (NPDES,
X, T, U, UX, UXX, UT),
where
NPDES Number
of equations.
(Input)
X Space
variable, x.
(Input)
T Time
variable, t.
(Input)
U Array of
length NPDES
containing the dependent variable values,
u.
(Input)
UX Array of
length NPDES
containing the first derivatives ux.
(Input)
UXX Array of
length NPDES
containing the second derivative uxx.
(Input)
UT Array of
length NPDES
containing the computed derivatives, ut.
(Output)
The name FCNUT must be declared EXTERNAL in the calling program.
FCNBC
User-supplied SUBROUTINE to evaluate
the boundary conditions. The boundary conditions accepted by MOLCH are αk uk + βk ux Ξ γk. Note: Users
must supply the values αk and βk, which
determine the values γk. Since the γk can depend on
t, values of γʹk are also
required. Users must supply these values. The usage is
CALL FCNBC (NPDES,
X, T, ALPHA, BTA, GAMMAP), where
NPDES Number
of equations. (Input)
X Space variable,
x. This value directs which boundary condition to compute.
(Input)
T
Time variable, t. (Input)
ALPHA Array of
length NPDES
containing the αk
values. (Output)
BTA Array of length
NPDES containing the βk
values. (Output)
GAMMAP Array of
length NPDES containing the values of the
derivatives, 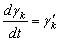
(Output)
The name FCNBC must be declared EXTERNAL in the calling program.
T Independent
variable, t. (Input/Output)
On input, T supplies the initial
time, t0. On output, T is set to the value
to which the integration has been updated. Normally, this new value is TEND.
TEND Value of t = tend at which the solution is desired. (Input)
XBREAK Array of
length NX
containing the break points for the cubic Hermite splines used in the x
discretization. (Input)
The points in the array XBREAK must be
strictly increasing. The values XBREAK(1) and XBREAK(NX) are the endpoints
of the interval.
Y Array of size
NPDES by NX containing the
solution. (Input/Output)
The array Y contains the
solution as Y(k, i)
= uk(x, tend) at x =
XBREAK(i). On
input, Y
contains the initial values. It MUST satisfy the boundary
conditions. On output, Y contains the
computed solution.
There is an optional application of MOLCH that uses
derivative values, ux(x, t0). The user
allocates twice the space for Y to pass this
information. The optional derivative information is input as
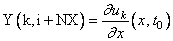
at x = X(i). The array Y contains the optional derivative values as output:

at x = X(i). To signal that this information is provided, use an options manager call as outlined in Comment 3 and illustrated in Examples 3 and 4.
Optional Arguments
NPDES Number of
differential equations. (Input)
Default: NPDES = size
(Y,1).
NX Number of
mesh points or lines. (Input)
Default: NX = size (Y,2).
TOL
Differential equation error tolerance. (Input)
An attempt is
made to control the local error in such a way that the global relative error is
proportional to TOL.
Default: TOL = 100. *
machine precision.
HINIT Initial
step size in the t integration. (Input)
This value must
be nonnegative. If HINIT is zero, an
initial step size of 0.001|tend t0| will be arbitrarily used. The step will
be applied in the direction of integration.
Default: HINIT = 0.0.
LDY Leading
dimension of Y
exactly as specified in the dimension statement of the calling
program. (Input)
Default: LDY = size (Y,1).
FORTRAN 90 Interface
Generic: CALL MOLCH (IDO, FCNUT, FCNBC, T, TEND, XBREAK, Y [, ])
Specific: The specific interface names are S_MOLCH and D_MOLCH.
FORTRAN 77 Interface
Single: CALL MOLCH (IDO, FCNUT, FCNBC, NPDES, T, TEND, NX, XBREAK, TOL, HINIT, Y, LDY)
Double: The double precision name is DMOLCH.
Description
Let M = NPDES, N = NX and xi = XBREAK(I). The routine MOLCH uses the method of lines to solve the partial differential equation system
Cubic Hermite polynomials are used in the x variable approximation so that the trial solution is expanded in the series
where ɸi(x) and Ψi(x) are the standard basis functions for the cubic Hermite polynomials with the knots x1 < x2 < < xN. These are piecewise cubic polynomials with continuous first derivatives. At the breakpoints, they satisfy
According to the collocation method, the coefficients of the approximation are obtained so that the trial solution satisfies the differential equation at the two Gaussian points in each subinterval,
for j = 1, , N. The collocation approximation to the differential equation is
for k = 1, , M and j = 1, , 2(N − 1).
This is a system of 2M(N − 1) ordinary differential equations in 2M N unknown coefficient functions, ai, k and bi, k. This system can be written in the matrix−vector form as A dc/dt = F (t, y) with c(t0) = c0 where c is a vector of coefficients of length 2M N and c0 holds the initial values of the coefficients. The last 2M equations are obtained by differentiating the boundary conditions
The initial conditions uk(x, t0) must satisfy the boundary conditions. Also, the γk(t) must be continuous and have a smooth derivative, or the boundary conditions will not be properly imposed for t > t0.
If αk = βk = 0, it is assumed that no boundary condition is desired for the k-th unknown at the left endpoint. A similar comment holds for the right endpoint. Thus, collocation is done at the endpoint. This is generally a useful feature for systems of first-order partial differential equations.
If the number of partial differential equations is M = 1 and the number of breakpoints is N = 4, then
c = [a1, b1, a2, b2, a3, b3, a4, b4]T
If M > 1, then each entry in the above matrix is replaced by an M Χ M diagonal matrix. The element α1 is replaced by diag(α1,1, , α1,M). The elements αN, β1 and βN are handled in the same manner. The ɸi(pj) and Ψi(pj) elements are replaced by ɸi(pj)IM and Ψi(pj)IM where IM is the identity matrix of order M. See Madsen and Sincovec (1979) for further details about discretization errors and Jacobian matrix structure.
The input/output array Y contains the values of the ak, i. The initial values of the bk, i are obtained by using the IMSL cubic spline routine CSINT (see Chapter 3, Interpolation and Approximation) to construct functions
The IMSL routine CSDER, see Chapter 3, Interpolation and Approximation, is used to approximate the values
There is an optional usage of MOLCH that allows the user to provide the initial values of bk, i.
The order of matrix A is 2M N and its maximum bandwidth is 6M 1. The band structure of the Jacobian of F with respect to c is the same as the band structure of A. This system is solved using a modified version of IVPAG. Some of the linear solvers were removed. Numerical Jacobians are used exclusively. The algorithm is unchanged. Gear's BDF method is used as the default because the system is typically stiff.
We now present four examples of PDEs that illustrate how users can interface their problems with IMSL PDE solving software. The examples are small and not indicative of the complexities that most practitioners will face in their applications. A set of seven sample application problems, some of them with more than one equation, is given in Sincovec and Madsen (1975). Two further examples are given in Madsen and Sincovec (1979).
Comments
1. Workspace may be explicitly provided, if desired, by use of M2LCH/DM2LCH. The reference is:
CALL M2LCH (IDO, FCNUT, FCNBC, NPDES, T, TEND, NX, XBREAK, TOL, HINIT, Y, LDY, WK, IWK)
The additional arguments are as follows:
WK Work array of length 2NX * NPDES(12 * NPDES2 + 21 * NPDES + 9). WK should not be changed between calls to M2LCH.
IWK Work array of length 2NX * NPDES. IWK should not be changed between calls to M2LCH.
4 1 After some initial success, the integration was halted by repeated error test failures.
4 2 On the next step, X + H will equal X. Either TOL is too small or the problem is stiff.
4 3 After some initial success, the integration was halted by a test on TOL.
4 4 Integration was halted after failing to pass the error test even after reducing the step size by a factor of 1.0E + 10. TOL may be too small.
4 5 Integration was halted after failing to achieve corrector convergence even after reducing the step size by a factor of 1.0E + 10. TOL may be too small.
3. Optional usage with Chapter 11 Option Manager
11 This
option consists of the parameter PARAM, an array with
50 components. See IVPAG for a more
complete documentation of the contents of this array. To reset this option, use
the subprogram SUMAG for single precision, and DUMAG (see Chapter 11, Utilities) for double precision. The
entry PARAM(1) is assigned
the initial step, HINIT. The entries PARAM(15) and PARAM(16) are assigned
the values equal to the number of lower and upper diagonals that will occur in
the Newton method for solving the BDF corrector equations. The value
PARAM(17) = 1 is used
to signal that the x derivatives of the initial data are provided in the
the array Y. The output values
PARAM(31)-PARAM(36) , showing
technical data about the ODE integration, are available with another option
manager subroutine call. This call is made after the storage for MOLCH is released. The
default values for the first 20 entries of PARAM are (0, 0, amach(2), 500., 0.,
5., 0, 0, 1., 3., 1., 2., 2., 1., amach(6), amach(6), 0, sqrt(amach(4)), 1., 0.).
Entries 2150 are defaulted to amach(6).
Example 1
The normalized linear diffusion PDE, ut = uxx, 0 x
1,
t > t0, is solved. The
initial values are
t0 = 0,
u(x, t0) = u0 = 1. There is a
zero-flux boundary condition at x = 1, namely ux(1, t) = 0,
(t > t0). The boundary value
of u(0, t) is abruptly changed from u0 to the value
u1 = 0.1. This transition
is completed by t = tδ = 0.09.
Due to restrictions in the type of boundary conditions sucessfully processed by MOLCH, it is necessary to provide the derivative boundary value function ʹ at x = 0 and at x = 1. The function at x = 0 makes a smooth transition from the value u0 at t = t0 to the value u1 at t = tδ. We compute the transition phase for ʹ by evaluating a cubic interpolating polynomial. For this purpose, the function subprogram CSDER, see Chapter 3, Interpolation and Approximation, is used. The interpolation is performed as a first step in the user-supplied routine FCNBC. The function and derivative values ( t0) = u0, ʹ (t0) = 0, ( tδ) = u1, and ʹ (tδ) = 0, are used as input to routine C2HER, to obtain the coefficients evaluated by CSDER. Notice that ʹ (t) = 0, t > tδ. The evaluation routine CSDER will not yield this value so logic in the routine FCNBC assigns ʹ (t) = 0, t > tδ.
! SPECIFICATIONS FOR LOCAL VARIABLES
PARAMETER (NPDES=1, NX=8, LDY=NPDES)
! SPECIFICATIONS FOR LOCAL VARIABLES
INTEGER I, IDO, J, NOUT, NSTEP
REAL HINIT, PREC, T, TEND, TOL, XBREAK(NX), Y(LDY,NX), U0
! SPECIFICATIONS FOR INTRINSICS
! SPECIFICATIONS FOR SUBROUTINES
! SPECIFICATIONS FOR FUNCTIONS
! This puts more output for small
! t values where action is fastest.
CALL MOLCH (IDO, FCNUT, FCNBC,
T, TEND, XBREAK, Y, TOL=TOL,
&
HINIT=HINIT)
WRITE (TITLE,'(A,F4.2)') 'Solution at T =', T
! Final call to release workspace
SUBROUTINE FCNUT (NPDES, X, T, U, UX, UXX, UT)
! SPECIFICATIONS FOR ARGUMENTS
REAL X, T, U(*), UX(*), UXX(*), UT(*)
SUBROUTINE FCNBC (NPDES, X, T, ALPHA, BTA, GAMP)
! SPECIFICATIONS FOR ARGUMENTS
REAL X, T, ALPHA(*), BTA(*), GAMP(*)
! SPECIFICATIONS FOR PARAMETERS
PARAMETER (TDELTA=0.09, U0=1.0, U1=0.1)
! SPECIFICATIONS FOR LOCAL VARIABLES
REAL DFDATA(2), FDATA(2), XDATA(2)
! SPECIFICATIONS FOR SAVE VARIABLES
! SPECIFICATIONS FOR SUBROUTINES
! Define the boundary conditions
! compute nonzero gamma prime.
IF (T .LE. TDELTA) GAMP(1) = CSDER(1,T,BREAK,CSCOEF)
! Compute the boundary layer data.
! Do Hermite cubic interpolation.
CALL C2HER (NDATA, XDATA, FDATA, DFDATA, BREAK, CSCOEF, IWK)
Output
Solution at T =0.01
1
2 3
4
5 6
7 8
0.969 0.997
1.000 1.000 1.000 1.000
1.000
1.000
Solution at T =0.04
1
2 3
4 5
6 7
8
0.625 0.871 0.963 0.991
0.998 1.000 1.000
1.000
Solution at T =0.09
1
2
3
4
5
6
7 8
0.0998
0.4603 0.7171 0.8673 0.9437
0.9781 0.9917
0.9951
Solution at T =0.16
1
2
3
4
5
6
7 8
0.0994
0.3127 0.5069 0.6680 0.7893
0.8708 0.9168
0.9316
Solution at T =0.25
1
2
3
4
5
6
7 8
0.0994
0.2564 0.4043 0.5352 0.6428
0.7223 0.7709
0.7873
Solution at T =0.36
1
2
3
4
5
6
7 8
0.0994
0.2172 0.3289 0.4289 0.5123
0.5749 0.6137
0.6268
Solution at T =0.49
1
2
3
4
5
6
7 8
0.0994
0.1847 0.2657 0.3383 0.3989
0.4445 0.4728
0.4824
Solution at T =0.64
1
2
3
4
5
6
7 8
0.0994
0.1583 0.2143 0.2644 0.3063
0.3379 0.3574
0.3641
Solution at T =0.81
1
2
3
4
5
6
7 8
0.0994
0.1382 0.1750 0.2080 0.2356
0.2563 0.2692
0.2736
Solution at T =1.00
1
2
3
4
5
6
7 8
0.0994
0.1237 0.1468 0.1674 0.1847
0.1977 0.2058 0.2085
Additonal Examples
Example 2
In this example, using MOLCH, we solve the linear normalized diffusion PDE ut = uxx but with an optional usage that provides values of the derivatives, ux, of the initial data. Due to errors in the numerical derivatives computed by spline interpolation, more precise derivative values are required when the initial data is u(x, 0) = 1 + cos[(2n 1)x], n > 1. The boundary conditions are zero flux conditions ux(0, t) = ux(1, t) = 0 for t > 0. Note that the initial data is compatible with these end conditions since the derivative function
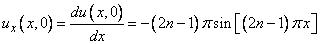
vanishes at x = 0 and x = 1.
The example illustrates the use of the IMSL options manager subprograms SUMAG or, for double precision, DUMAG, see Chapter 11, Utilities, to reset the array PARAM used for control of the specialized version of IVPAG that integrates the system of ODEs. This optional usage signals that the derivative of the initial data is passed by the user. The values u(x, tend) and ux(x, tend) are output at the breakpoints with the optional usage.
USE IMSL_LIBRARIES
IMPLICIT NONE
! SPECIFICATIONS FOR LOCAL VARIABLES
INTEGER LDY, NPDES, NX, IAC
PARAMETER (NPDES=1, NX=10, LDY=NPDES)
! SPECIFICATIONS FOR PARAMETERS
INTEGER ICHAP, IGET, IPUT, KPARAM
PARAMETER (ICHAP=5, IGET=1, IPUT=2, KPARAM=11)
! SPECIFICATIONS FOR LOCAL VARIABLES
INTEGER I, IACT, IDO, IOPT(1), J, JGO, N, NOUT, NSTEP
REAL ARG1, HINIT, PREC, PARAM(50), PI, T, TEND, TOL, &
XBREAK(NX), Y(LDY,2*NX)
CHARACTER TITLE*36
! SPECIFICATIONS FOR INTRINSICS
INTRINSIC COS, FLOAT, SIN, SQRT
REAL COS, FLOAT, SIN, SQRT
! SPECIFICATIONS FOR FUNCTIONS
EXTERNAL FCNBC, FCNUT
! Set breakpoints and initial
! conditions.
N = 5
PI = CONST('pi')
IOPT(1) = KPARAM
DO 10 I=1, NX
XBREAK(I) = FLOAT(I-1)/(NX-1)
ARG1 = (2.*N-1)*PI
! Set function values.
Y(1,I) = 1. + COS(ARG1*XBREAK(I))
! Set first derivative values.
Y(1,I+NX) = -ARG1*SIN(ARG1*XBREAK(I))
10 CONTINUE
! Set parameters for MOLCH
PREC = AMACH(4)
TOL = SQRT(PREC)
HINIT = 0.01*TOL
T = 0.0
IDO = 1
NSTEP = 10
CALL UMACH (2, NOUT)
J = 0
! Get and reset the PARAM array
! so that user-provided derivatives
! of the initial data are used.
JGO = 1
IACT = IGET
GO TO 70
20 CONTINUE
! This flag signals that
! derivatives are passed.
PARAM(17) = 1.
JGO = 2
IACT = IPUT
GO TO 70
30 CONTINUE
! Look at output at steps
! of 0.001.
TEND = 0.
40 CONTINUE
J = J + 1
TEND = TEND + 0.001
! Solve the problem
CALL MOLCH (IDO, FCNUT, FCNBC, T, TEND, XBREAK, Y, NPDES=NPDES, &
NX=NX, HINIT=HINIT, TOL=TOL)
IF (J .LE. NSTEP) THEN
! Print results
WRITE (TITLE,'(A,F5.3)') 'Solution and derivatives at T =', T
CALL WRRRN (TITLE, Y)
! Final call to release workspace
IF (J .EQ. NSTEP) IDO = 3
GO TO 40
END IF
! Show, for example, the maximum
! step size used.
JGO = 3
IACT = IGET
GO TO 70
50 CONTINUE
WRITE (NOUT,*) ' Maximum step size used is: ', PARAM(33)
! Reset option to defaults
JGO = 4
IAC = IPUT
IOPT(1) = -IOPT(1)
GO TO 70
60 CONTINUE
! RETURN
! Internal routine to work options
70 CONTINUE
CALL SUMAG ('math', ICHAP, IACT, IOPT, PARAM, numopt=1)
GO TO (20, 30, 50, 60), JGO
END
SUBROUTINE FCNUT (NPDES, X, T, U, UX, UXX, UT)
! SPECIFICATIONS FOR ARGUMENTS
INTEGER NPDES
REAL X, T, U(*), UX(*), UXX(*), UT(*)
!
! Define the PDE
UT(1) = UXX(1)
! RETURN
END
SUBROUTINE FCNBC (NPDES, X, T, ALPHA, BTA, GAMP)
! SPECIFICATIONS FOR ARGUMENTS
INTEGER NPDES
REAL X, T, ALPHA(*), BTA(*), GAMP(*)
!
ALPHA(1) = 0.0
BTA(1) = 1.0
GAMP(1) = 0.0
! RETURN
END
Output
Solution and derivatives at T =0.001
1 2
3 4
5 6
7
8 9
10
1.483 0.517 1.483 0.517
1.483 0.517 1.483 0.517 1.483
0.517
11
12 13
14 15
16 17
18 19
20
0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000
0.000
Solution
and derivatives at T =0.002
1 2
3 4
5 6
7 8
9 10
1.233 0.767 1.233
0.767 1.233 0.767 1.233 0.767
1.233 0.767
11
12 13
14 15
16 17
18 19
20
0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000
0.000
Solution and derivatives at T =0.003
1 2
3 4
5 6
7 8
9 10
1.113 0.887 1.113
0.887 1.113 0.887 1.113 0.887
1.113 0.887
11
12 13
14 15
16 17
18 19
20
0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000
0.000
Solution and derivatives at T =0.004
1 2
3
4 5
6 7
8 9
10
1.054 0.946 1.054 0.946
1.054 0.946 1.054 0.946 1.054
0.946
11
12 13
14 15
16 17
18 19
20
0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000
0.000
Solution and derivatives at T =0.005
1 2
3 4
5 6
7 8
9 10
1.026 0.974 1.026
0.974 1.026 0.974 1.026 0.974
1.026 0.974
11
12 13 14
15
16 17
18 19
20
0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000
0.000
Solution and derivatives at T =0.006
1 2
3 4
5 6
7 8
9 10
1.012 0.988 1.012
0.988 1.012 0.988 1.012 0.988
1.012 0.988
11
12 13
14 15
16 17
18 19
20
0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000
0.000
Solution and derivatives at T =0.007
1 2
3 4
5 6
7 8
9 10
1.006 0.994 1.006
0.994 1.006 0.994 1.006 0.994
1.006 0.994
11
12 13
14 15
16 17
18 19
20
0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000
0.000
Solution and derivatives at T =0.008
1 2
3 4
5 6
7 8
9 10
1.003 0.997 1.003
0.997 1.003 0.997 1.003 0.997
1.003 0.997
11
12 13
14 15
16 17
18 19
20
0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000
0.000
Solution and derivatives at T =0.009
1 2
3 4
5 6 7
8
9 10
1.001 0.999 1.001
0.999 1.001 0.999 1.001 0.999
1.001 0.999
11
12 13
14 15
16 17
18 19
20
0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000
0.000
Solution and derivatives at T
=0.010
1
2 3
4 5
6 7
8 9
10
1.001 0.999 1.001 0.999
1.001 0.999 1.001 0.999 1.001
0.999
11
12 13
14 15
16 17
18 19
20
0.000 0.000 0.000 0.000
0.000 0.000 0.000 0.000 0.000
0.000
Maximum step size used is:
1.00000E-02
Example 3
In this example, we consider the linear normalized
hyperbolic PDE, utt = uxx, the vibrating
string equation. This naturally leads to a system of first order PDEs. Define a
new dependent variable
ut = v. Then,
vt = uxx is the second
equation in the system. We take as initial data u(x, 0) =
sin(x) and ut(x, 0) =
v(x, 0) = 0. The ends of the string are fixed so u(0,
t) = u(1, t) = v(0, t) =
v(1, t) = 0. The exact solution to this problem is
u(x, t) = sin(x) cos(t). Residuals are
computed at the output values of t for 0 < t 2. Output is
obtained at 200 steps in increments of 0.01.
Even though the sample code MOLCH gives satisfactory results for this PDE, users should be aware that for nonlinear problems, shocks can develop in the solution. The appearance of shocks may cause the code to fail in unpredictable ways. See Courant and Hilbert (1962), pages 488-490, for an introductory discussion of shocks in hyperbolic systems.
USE IMSL_LIBRARIES
IMPLICIT NONE
! SPECIFICATIONS FOR LOCAL VARIABLES
INTEGER LDY, NPDES, NX
PARAMETER (NPDES=2, NX=10, LDY=NPDES)
! SPECIFICATIONS FOR PARAMETERS
INTEGER ICHAP, IGET, IPUT, KPARAM
PARAMETER (ICHAP=5, IGET=1, IPUT=2, KPARAM=11)
! SPECIFICATIONS FOR LOCAL VARIABLES
INTEGER I, IACT, IDO, IOPT(1), J, JGO, NOUT, NSTEP
REAL HINIT, PREC, PARAM(50), PI, T, TEND, TOL, XBREAK(NX), &
Y(LDY,2*NX), ERROR(NX), ERRU
! SPECIFICATIONS FOR INTRINSICS
INTRINSIC COS, FLOAT, SIN, SQRT
REAL COS, FLOAT, SIN, SQRT
! SPECIFICATIONS FOR SUBROUTINES
! SPECIFICATIONS FOR FUNCTIONS
EXTERNAL FCNBC, FCNUT
! Set breakpoints and initial
! conditions.
PI = CONST('pi')
IOPT(1) = KPARAM
DO 10 I=1, NX
XBREAK(I) = FLOAT(I-1)/(NX-1)
! Set function values.
Y(1,I) = SIN(PI*XBREAK(I))
Y(2,I) = 0.
! Set first derivative values.
Y(1,I+NX) = PI*COS(PI*XBREAK(I))
Y(2,I+NX) = 0.0
10 CONTINUE
! Set parameters for MOLCH
PREC = AMACH(4)
TOL = 0.1*SQRT(PREC)
HINIT = 0.01*TOL
T = 0.0
IDO = 1
NSTEP = 200
CALL UMACH (2, NOUT)
J = 0
! Get and reset the PARAM array
! so that user-provided derivatives
! of the initial data are used.
JGO = 1
IACT = IGET
GO TO 90
20 CONTINUE
! This flag signals that
! derivatives are passed.
PARAM(17) = 1.
JGO = 2
IACT = IPUT
GO TO 90
30 CONTINUE
! Look at output at steps
! of 0.01 and compute errors.
ERRU = 0.
TEND = 0.
40 CONTINUE
J = J + 1
TEND = TEND + 0.01
! Solve the problem
CALL MOLCH (IDO, FCNUT, FCNBC, T, TEND, XBREAK, Y, NX=NX, &
HINIT=HINIT, TOL=TOL)
DO 50 I=1, NX
ERROR(I) = Y(1,I) - SIN(PI*XBREAK(I))*COS(PI*TEND)
50 CONTINUE
IF (J .LE. NSTEP) THEN
DO 60 I=1, NX
ERRU = AMAX1(ERRU,ABS(ERROR(I)))
60 CONTINUE
! Final call to release workspace
IF (J .EQ. NSTEP) IDO = 3
GO TO 40
END IF
! Show, for example, the maximum
! step size used.
JGO = 3
IACT = IGET
GO TO 90
70 CONTINUE
WRITE (NOUT,*) ' Maximum error in u(x,t) divided by TOL: ', &
ERRU/TOL
WRITE (NOUT,*) ' Maximum step size used is: ', PARAM(33)
! Reset option to defaults
JGO = 4
IACT = IPUT
IOPT(1) = -IOPT(1)
GO TO 90
80 CONTINUE
! RETURN
! Internal routine to work options
90 CONTINUE
CALL SUMAG ('math', ICHAP, IACT, IOPT, PARAM)
GO TO (20, 30, 70, 80), JGO
END
SUBROUTINE FCNUT (NPDES, X, T, U, UX, UXX, UT)
! SPECIFICATIONS FOR ARGUMENTS
INTEGER NPDES
REAL X, T, U(*), UX(*), UXX(*), UT(*)
!
! Define the PDE
UT(1) = U(2)
UT(2) = UXX(1)
! RETURN
END
SUBROUTINE FCNBC (NPDES, X, T, ALPHA, BTA, GAMP)
! SPECIFICATIONS FOR ARGUMENTS
INTEGER NPDES
REAL X, T, ALPHA(*), BTA(*), GAMP(*)
!
ALPHA(1) = 1.0
BTA(1) = 0.0
GAMP(1) = 0.0
ALPHA(2) = 1.0
BTA(2) = 0.0
GAMP(2) = 0.0
! RETURN
END
Output
Maximum error in u(x,t) divided by
TOL: 1.28094
Maximum step size used
is: 9.99999E-02
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |