Invokes a module, with the statement USE PDE_1D_MG, near the second line of the program unit. The integrator is provided with single or double precision arithmetic, and a generic named interface is provided. We do not recommend using 32-bit floating point arithmetic here. The routine is called within the following loop, and is entered with each value of IDO. The loop continues until a value of IDO results in an exit.
IDO=1
DO
CASE(IDO == 1) {Do required initialization steps}
CASE(IDO == 2) {Save solution, update T0 and TOUT }
IF{Finished with integration} IDO=3
CASE(IDO == 3) EXIT {Normal}
CASE(IDO == 4) EXIT {Due to errors}
CASE(IDO == 5) {Evaluate initial data}
CASE(IDO == 6) {Evaluate differential equations}
CASE(IDO == 7) {Evaluate boundary conditions}
CASE(IDO == 8) {Prepare to solve banded system}
CASE(IDO == 9) {Solve banded system}
CALL PDE_1D_MG (T0,
TOUT, IDO, U, &
initial_conditions,&
pde_system_definition,&
boundary_conditions,
IOPT)
END DO
The arguments to PDE_1D_MG are required or optional.
Required Arguments
T0—(Input/Output)
This
is the value of the independent variable t where the integration of
ut begins. It is set to the value TOUT on return.
TOUT—(Input)
This
is the value of the independent variable t where the integration of
ut ends. Note: Values of T0 < TOUT imply
integration in the forward direction, while values of
T0 > TOUT imply
integration in the backward direction. Either direction is permitted.
IDO—(Input/Output)
This
in an integer flag that directs program control and user action. Its value
is used for initialization, termination, and for directing user response during
reverse communication:
IDO=1 This value is assigned by the user for the start of a new problem. Internally it causes allocated storage to be reallocated, conforming to the problem size. Various initialization steps are performed.
IDO=2 This value is assigned by the routine when the integrator has successfully reached the end point, TOUT.
IDO=3 This value is assigned by the user at the end of a problem. The routine is called by the user with this value. Internally it causes termination steps to be performed.
IDO=4 This value is assigned by the integrator when a type FATAL or TERMINAL error condition has occurred, and error processing is set NOT to STOP for these types of errors. It is not necessary to make a final call to the integrator with IDO=3 in this case.
Values of IDO = 5,6,7,8,9 are reserved for applications that provide problem information or linear algebra computations using reverse communication. When problem information is provided using reverse communication, the differential equations, boundary conditions and initial data must all be given. The absence of optional subroutine names in the calling sequence directs the routine to use reverse communication. In the module PDE_1D_MG_INT, scalars and arrays for evaluating results are named below. The names are preceded by the prefix “s_pde_1d_mg_” or “d_pde_1d_mg_”, depending on the precision. We use the prefix “?_pde_1d_mg_”, for the appropriate choice.
IDO=5 This value is assigned by the integrator, requesting data for the initial conditions. Following this evaluation the integrator is re-entered.
(Optional) Update the grid of values in array locations U(NPDE +1, j) j = 2, ¼, N. This grid is returned to the user equally spaced, but can be updated as desired, provided the values are increasing.
(Required) Provide initial values for all components of the system at the grid of values U(NPDE +1, j) j = 1, ¼, N. If the optional step of updating the initial grid is performed, then the initial values are evaluated at the updated grid.
IDO=6 This value is assigned by the integrator, requesting data
for the differential equations. Following this evaluation the integrator
is re-entered. Evaluate the terms of the system of Equation 2. A
default value of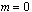 
is assumed, but this can be changed to one of the other
choices 
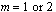. Use the
optional argument IOPT(:) for that
purpose. Put the values in the arrays as indicated[1].
If any of the functions cannot be evaluated, set pde_1d_mg_ires=3. Otherwise do not change its value.
IDO=7 This value is assigned by the integrator, requesting data for the boundary conditions, as expressed in Equation 3. Following the evaluation the integrator is re-entered.
The value xÎ{xL, xR}, and the logical flag pde_1d_mg_LEFT=.TRUE. for x = xL. It has the value pde_1d_mg_LEFT=.FALSE. for x = xR. If any of the functions cannot be evaluated, set pde_1d_mg_ires=3. Otherwise do not change its value.
IDO=8 This value is assigned by the integrator, requesting the calling program to prepare for solving a banded linear system of algebraic equations. This value will occur only when the option for “reverse communication solving” is set in the array IOPT(:), with option PDE_1D_MG_REV_COMM_FACTOR_SOLVE. The matrix data for this system is in Band Storage Mode, described in the section: Reference Material for the IMSL Fortran Numerical Libraries.
|
PDE_1D_MG_IBAND |
Half band-width of linear system |
|
PDE_1D_MG_LDA |
The value 3*PDE_1D_MG_IBAND+1, with NEQ = (NPDE+1)N |
|
?_PDE_1D_MG_A |
Array of size PDE_1D_MG_LDA by NEQ holding the problem matrix in Band Storage Mode |
|
PDE_1D_MG_PANIC_FLAG |
Integer set to a non-zero value only if the linear system is detected as singular |
IDO=9 This value is assigned by the integrator , requesting the calling program to solve a linear system with the matrix defined as noted with IDO=8.
|
?_PDE_1D_MG_RHS |
Array of size NEQ holding the linear system problem right-hand side |
|
PDE_1D_MG_PANIC_FLAG |
Integer set to a non-zero value only if the linear system is singular |
|
?_PDE_1D_MG_SOL |
Array of size NEQ to receive the solution, after the solving step |
U(1:NPDE+1,1:N)—(Input/Output)
This
assumed-shape array specifies Input information about the problem size
and boundaries. The dimension of the problem is obtained from NPDE
+1 = size(U,1). The number of grid points is obtained by N
= size(U,2). Limits for the variable x are assigned as input
in array locations, U(NPDE +1, 1) = xL, U(NPDE +1, N)
=xR. It is not required to define U(NPDE +1,
j), j=2, ¼,
N-1. At completion, the array U(1:NPDE,1:N)contains
the approximate solution value
Ui(xj(TOUT),TOUT) in location U(I,J). The grid
value xj(TOUT) is in location U(NPDE+1,J).
Normally the grid values are equally spaced as the integration starts.
Variable spaced grid values can be provided by defining them as Output
from the subroutine initial_conditions or
during reverse communication, IDO=5.
Optional Arguments
initial_conditions—(Input)
The
name of an external subroutine, written by the user, when using forward
communication. If this argument is not used, then reverse communication is
used to provide the problem information. The routine gives the initial
values for the system at the starting independent variable value T0. This routine
can also provide a non-uniform grid at the initial value.
SUBROUTINE initial_conditions (NPDE,N,U)
Integer NPDE,N
REAL(kind(T0)) U(:,)
END SUBROUTINE
(Optional)
Update the grid of values in array locations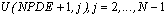 
. This grid is input equally
spaced, but can be updated as desired, provided the values are increasing.
(Required)
Provide initial values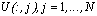 
for all components of the system at the grid of values
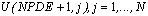. If the optional
step of updating the initial grid is performed, then the initial values are
evaluated at the updated grid.
pde_system_definition—(Input)
The name of an
external subroutine, written by the user, when using forward
communication. It gives the differential equation, as expressed in
Equation 2.
Evaluate the terms of the system of . A
default value of 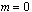is assumed, but this can be changed to one of the other
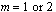choices . Use the
optional argument IOPT(:)
for that purpose. Put the values in the arrays as indicated.
If any of the functions cannot be evaluated, set ires=3. Otherwise do not change its value.
boundary_conditions—(Input)
The
name of an external subroutine, written by the user when using forward
communication. It gives the boundary conditions, as expressed in Equation
2.
SUBROUTINE BOUNDARY_CONDITIONS(T,BETA,GAMMA,U,DUDX,NPDE,LEFT,IRES)
real(kind(1d0)),intent(in)::t
real(kind(1d0)),intent(out),dimension(:)::BETA, GAMMA
real(kind(1d0)),intent(in),dimension(:)::U,DUDX
integer,intent(in)::NPDE
logical,intent(in)::LEFT
integer,intent(out)::IRES
END SUBROUTINE
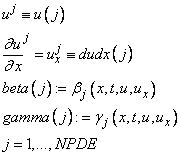
The value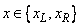 
, and the logical flag LEFT=.TRUE.
for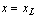 
. The flag has
the value LEFT=.FALSE.
for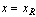 
.
IOPT—(Input)
Derived type
array s_options
or d_options,
used for passing optional data to PDE_1D_MG. See
the section Optional Data in the Introduction for
an explanation of the derived type and its use. It is necessary to invoke
a module, with the statement USE
ERROR_OPTION_PACKET, near the second line of the program unit.
Examples 2-8 use this optional argument. The choices are as follows:
|
Packaged Options for PDE_1D_MG | ||
|
Option Prefix = ? |
Option Name |
Option Value |
|
S_, d_ |
PDE_1D_MG_CART_COORDINATES |
1 |
|
S_, d_ |
PDE_1D_MG_CYL_COORDINATES |
2 |
|
S_, d_ |
PDE_1D_MG_SPH_COORDINATES |
3 |
|
S_, d_ |
PDE_1D_MG_TIME_SMOOTHING |
4 |
|
S_, d_ |
PDE_1D_MG_SPATIAL_SMOOTHING |
5 |
|
S_, d_ |
PDE_1D_MG_MONITOR_REGULARIZING |
6 |
|
S_, d_ |
PDE_1D_MG_RELATIVE_TOLERANCE |
7 |
|
S_, d_ |
PDE_1D_MG_ABSOLUTE_TOLERANCE |
8 |
|
S_, d_ |
PDE_1D_MG_MAX_BDF_ORDER |
9 |
|
S_, d_ |
PDE_1D_MG_REV_COMM_FACTOR_SOLVE |
10 |
|
s_, d_ |
PDE_1D_MG_NO_NULLIFY_STACK |
11 |
IOPT(IO) =
PDE_1D_MG_CART_COORDINATES
Use the value 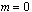in Equation 2. This is the
default.
IOPT(IO) =
PDE_1D_MG_CYL_COORDINATES
Use the value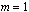 
in Equation 2. The default
value is .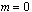
IOPT(IO) =
PDE_1D_MG_SPH_COORDINATES
Use the value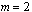 
in Equation 2. The default
value is .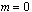
IOPT(IO) =
?_OPTIONS(PDE_1D_MG_TIME_SMOOTHING,TAU)
This option resets the
value of the parameter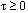 
, described
above.
The default value is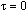 
.
IOPT(IO) =
?_OPTIONS(PDE_1D_MG_SPATIAL_SMOOTHING,KAP)
This option resets the
value of the parameter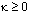 
, described
above.
The default value is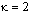 
.
IOPT(IO) =
?_OPTIONS(PDE_1D_MG_MONITOR_REGULARIZING,ALPH)
This option resets
the value of the parameter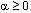 
,
described above.
The default value is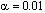 
.
IOPT(IO) =
?_OPTIONS
(PDE_1D_MG_RELATIVE_TOLERANCE,RTOL)
This option resets
the value of the relative accuracy parameter used in DASPG. The
default value is RTOL=1E-2 for single
precision and
RTOL=1D-4 for double
precision.
IOPT(IO) =
?_OPTIONS
(PDE_1D_MG_ABSOLUTE_TOLERANCE,ATOL)
This option resets
the value of the absolute accuracy parameter used in DASPG. The
default value is ATOL=1E-2 for single
precision and
ATOL=1D-4 for double
precision.
IOPT(IO) =
PDE_1D_MG_MAX_BDF_ORDER
IOPT(IO+1) = MAXBDF
Reset the maximum order
for the BDF
formulas used in DASPG. The
default value is MAXBDF=2. The
new value can be any integer between 1 and 5. Some problems will benefit
by making this change. We used the default value due to the fact that
DASPG may cycle
on its selection of order and step-size with orders higher than value 2.
IOPT(IO) =
PDE_1D_MG_REV_COMM_FACTOR_SOLVE
The calling program unit will solve
the banded linear systems required in the stiff differential-algebraic equation
integrator. Values of IDO=8, 9 will occur only when this optional
value is used.
IOPT(IO) =
PDE_1D_MG_NO_NULLIFY_STACK
To maintain an efficient interface, the
routine PDE_1D_MG collapses
the subroutine call stack with CALL_E1PSH(“NULLIFY_STACK”).
This implies that the overhead of maintaining the stack will be eliminated,
which may be important with reverse communication. It does not eliminate
error processing. However, precise information of which routines have
errors will not be displayed. To see the full call chain, this option
should be used. Following completion of the integration, stacking is
turned back on with CALL_E1POP(“NULLIFY_STACK”).
FORTRAN 90 Interface
Generic: CALL PDE_1D_MG (T0, TOUT, IDO, [,…])
Specific: The specific interface names are S_PDE_1D_MG and D_PDE_1D_MG.
Description
The equation
,
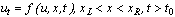is approximated at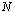 
time-dependent grid values
.
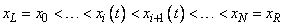Using the total differential
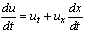
transforms the differential equation to
.
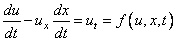Using central divided differences for the factor ux leads to the system of ordinary differential equations in implicit form
.
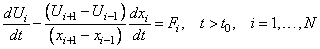The terms Ui, Fi respectively represent the approximate solution to the partial differential equation and the value of f(u,x,t) at the point (x,t) = (xi,(t),t). The truncation error is second-order in the space variable, x. The above ordinary differential equations are underdetermined, so additional equations are added for the variation of the time-dependent grid points. It is necessary to discuss these equations, since they contain parameters that can be adjusted by the user. Often it will be necessary to modify these parameters to solve a difficult problem. For this purpose the following quantities are defined[2]:
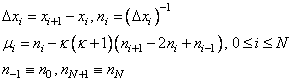
The values ni are the
so-called point concentration of the grid, and 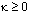denotes a spatial smoothing
parameter. Now the grid points are defined implicitly so that
,
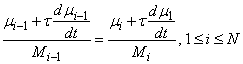where τ ≥ 1 is a time-smoothing parameter. Choosing τ very large results in a fixed grid. Increasing the value of τ from its default avoids the error condition where grid lines cross. The divisors are
.
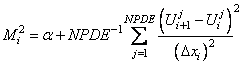The value κ determines the level of clustering or spatial smoothing of the grid points. Decreasing κ from its default decrease the amount of spatial smoothing. The parameters Mi approximate arc length and help determine the shape of the grid or xi-distribution. The parameter τ prevents the grid movement from adjusting immediately to new values of the Mi, thereby avoiding oscillations in the grid that cause large relative errors. This is important when applied to solutions with steep gradients.
The discrete form of the differential equation and the smoothing equations are combined to yield the implicit system of differential equations. κ
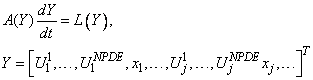
This is frequently a stiff differential-algebraic system. It is solved using the integrator DASPG and its subroutines, including D2SPG. These are documented in this chapter. Note that DASPG is restricted to use within PDE_1D_MG until the routine exits with the flag IDO = 3. If DASPG is needed during the evaluations of the differential equations or boundary conditions, use of a second processor and inter-process communication is required. The only options for DASPG set by PDE_1D_MG are the Maximum BDF Order, and the absolute and relative error values, ATOL and RTOL. Users may set other options using the Options Manager. This is described in routine DASPG and generally in Chapter 11 of this manual.
Remarks on the Examples
Due to its importance and the complexity of its interface, this subroutine is presented with several examples. Many of the program features are exercised. The problems complete without any change to the optional arguments, except where these changes are required to describe or to solve the problem.
In many applications the solution to a PDE is used as an auxiliary variable, perhaps as part of a larger design or simulation process. The truncation error of the approximate solution is commensurate with piece-wise linear interpolation on the grid of values, at each output point. To show that the solution is reasonable, a graphical display is revealing and helpful. We have not provided graphical output as part of our documentation, but users may already have the Visual Numerics, Inc. product, PV-WAVE, not included with Fortran Numerical Library. Examples 1-8 write results in files “PDE_ex0?.out” that can be visualized with PV-WAVE. We provide a script of commands, “pde_1d_mg_plot.pro”, for viewing the solutions (see example below). The grid of values and each consecutive solution component is displayed in separate plotting windows. The script and data files written by examples 1-8 on a SUN-SPARC system are in the directory for Fortran Numerical Library examples. When inside PV_WAVE, execute the command line “pde_1d_mg_plot,filename='PDE_ex0?.out'” to view the output of a particular example.
Code for PV-WAVE Plotting (Examples Directory)
PRO PDE_1d_mg_plot, FILENAME = filename, PAUSE = pause
;
if keyword_set(FILENAME) then file = filename else file = "res.dat"
if keyword_set(PAUSE) then twait = pause else twait = .1
;
; Define floating point variables that will be read
; from the first line of the data file.
xl = 0D0
xr = 0D0
t0 = 0D0
tlast = 0D0
;
; Open the data file and read in the problem parameters.
openr, lun, filename, /get_lun
readf, lun, npde, np, nt, xl, xr, t0, tlast
; Define the arrays for the solutions and grid.
u = dblarr(nt, npde, np)
g = dblarr(nt, np)
times = dblarr(nt)
;
; Define a temporary array for reading in the data.
tmp = dblarr(np)
t_tmp = 0D0
;
; Read in the data.
for i = 0, nt-1 do begin ; For each step in time
readf, lun, t_tmp
times(i) = t_tmp
for k = 0, npde-1 do begin ; For each PDE:
rmf, lun, tmp
u(i,k,*) = tmp ; Read in the components.
end
rmf, lun, tmp
g(i,*) = tmp ; Read in the grid.
end
;
; Close the data file and free the unit.
close, lun
free_lun, lun
;
; We now have all of the solutions and grids.
;
; Delete any window that is currently open.
while (!d.window NE -1) do WDELETE
;
; Open two windows for plotting the solutions
; and grid.
window, 0, xsize = 550, ysize = 420
window, 1, xsize = 550, ysize = 420
;
; Plot the grid.
wset, 0
plot, [xl, xr], [t0, tlast], /nodata, ystyle = 1, $
title = "Grid Points", xtitle = "X", ytitle = "Time"
for i = 0, np-1 do begin
oplot, g(*, i), times, psym = -1
end
;
; Plot the solution(s):
wset, 1
for k = 0, npde-1 do begin
umin = min(u(*,k,*))
umax = max(u(*,k,*))
for i = 0, nt-1 do begin
title = strcompress("U_"+string(k+1), /remove_all)+ $
" at time "+string(times(i))
plot, g(i, *), u(i,k,*), ystyle = 1, $
title = title, xtitle = "X", $
ytitle = strcompress("U_"+string(k+1), /remove_all), $
xr = [xl, xr], yr = [umin, umax], $
psym = -4
wait, twait
end
end
end
Example 1 - Electrodynamics Model
This example is from Blom and Zegeling (1994). The system is
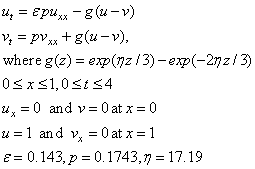
We make the connection between the model problem statement and the example:
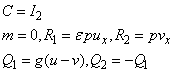
The boundary conditions are
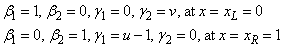
Rationale: Example 1
This is a non-linear problem with sharply changing
conditions near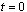 
.
The default settings of integration parameters allow the problem to be
solved. The use of PDE_1D_MG
with forward communication requires three subroutines provided by the user to
describe the initial conditions, differential equations, and boundary
conditions.
program PDE_EX1
! Electrodynamics Model:
USE PDE_1d_mg_int
IMPLICIT NONE
INTEGER, PARAMETER :: NPDE=2, N=51, NFRAMES=5
INTEGER I, IDO
! Define array space for the solution.
real(kind(1d0)) U(NPDE+1,N), T0, TOUT
real(kind(1d0)) :: ZERO=0D0, ONE=1D0, &
DELTA_T=10D0, TEND=4D0
EXTERNAL IC_01, PDE_01, BC_01
! Start loop to integrate and write solution values.
IDO=1
DO
SELECT CASE (IDO)
! Define values that determine limits.
CASE (1)
T0=ZERO
TOUT=1D-3
U(NPDE+1,1)=ZERO;U(NPDE+1,N)=ONE
OPEN(FILE='PDE_ex01.out',UNIT=7)
WRITE(7, "(3I5, 4F10.5)") NPDE, N, NFRAMES,&
U(NPDE+1,1), U(NPDE+1,N), T0, TEND
! Update to the next output point.
! Write solution and check for final point.
CASE (2)
WRITE(7,"(F10.5)")TOUT
DO I=1,NPDE+1
WRITE(7,"(4E15.5)")U(I,:)
END DO
T0=TOUT;TOUT=TOUT*DELTA_T
IF(T0 >= TEND) IDO=3
TOUT=MIN(TOUT, TEND)
! All completed. Solver is shut down.
CASE (3)
CLOSE(UNIT=7)
EXIT
END SELECT
! Forward communication is used for the problem data.
CALL PDE_1D_MG (T0, TOUT, IDO, U,&
initial_conditions= IC_01,&
PDE_system_definition= PDE_01,&
boundary_conditions= BC_01)
END DO
END
SUBROUTINE IC_01(NPDE, NPTS, U)
! This is the initial data for Example 1.
IMPLICIT NONE
INTEGER NPDE, NPTS
REAL(KIND(1D0)) U(NPDE+1,NPTS)
U(1,:)=1D0;U(2,:)=0D0
END SUBROUTINE
SUBROUTINE PDE_01(T, X, NPDE, U, DUDX, C, Q, R, IRES)
! This is the differential equation for Example 1.
IMPLICIT NONE
INTEGER NPDE, IRES
REAL(KIND(1D0)) T, X, U(NPDE), DUDX(NPDE),&
C(NPDE,NPDE), Q(NPDE), R(NPDE)
REAL(KIND(1D0)) :: EPS=0.143D0, P=0.1743D0,&
ETA=17.19D0, Z, TWO=2D0, THREE=3D0
C=0D0;C(1,1)=1D0;C(2,2)=1D0
R=P*DUDX;R(1)=R(1)*EPS
Z=ETA*(U(1)-U(2))/THREE
Q(1)=EXP(Z)-EXP(-TWO*Z)
Q(2)=-Q(1)
END SUBROUTINE
SUBROUTINE BC_01(T, BTA, GAMA, U, DUDX, NPDE, LEFT, IRES)
! These are the boundary conditions for Example 1.
IMPLICIT NONE
INTEGER NPDE, IRES
LOGICAL LEFT
REAL(KIND(1D0)) T, BTA(NPDE), GAMA(NPDE),&
U(NPDE), DUDX(NPDE)
IF(LEFT) THEN
BTA(1)=1D0;BTA(2)=0D0
GAMA(1)=0D0;GAMA(2)=U(2)
ELSE
BTA(1)=0D0;BTA(2)=1D0
GAMA(1)=U(1)-1D0;GAMA(2)=0D0
END IF
END SUBROUTINE
Additional Examples
Example 2 - Inviscid Flow on a Plate
This example is a first order system from Pennington and Berzins, (1994). The equations are
Following elimination of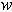 
, there remain
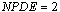differential equations. The
variable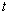 
is not time,
but a second space variable. The integration goes from 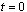to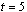 
. It is necessary to
truncate the variable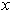 
at
a finite value, say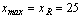
. In terms of the integrator, the system is defined by
letting 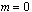and
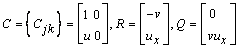
The boundary conditions are satisfied by
We use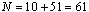 
grid points and output the solution at steps of 
.
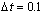Rationale: Example 2
This is a non-linear boundary layer problem with sharply
changing condition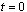s near . The problem statement was modified so that boundary
conditions are continuous near 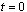. Without this change the underlying integration software,
DASPG,
cannot solve the problem. The continuous blending function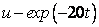 
is arbitrary and artfully
chosen. This is a mathematical change to the problem, required because of
the stated discontinuity at 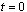. Reverse communication is used for the problem data.
No additional user-written subroutines are required when using reverse
communication. We also have chosen 10 of the initial grid points to be
concentrated near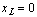 
,
anticipating rapid change in the solution near that point. Optional
changes are made to use a pure absolute error tolerance and non-zero
time-smoothing.
program PDE_1D_MG_EX02
! Inviscid Flow Over a Plate
USE PDE_1d_mg_int
USE ERROR_OPTION_PACKET
IMPLICIT NONE
INTEGER, PARAMETER :: NPDE=2, N1=10, N2=51, N=N1+N2
INTEGER I, IDO, NFRAMES
! Define array space for the solution.
real(kind(1d0)) U(NPDE+1,N), T0, TOUT, DX1, DX2, DIF
real(kind(1d0)) :: ZERO=0D0, ONE=1D0, DELTA_T=1D-1,&
TEND=5D0, XMAX=25D0
real(kind(1d0)) :: U0=1D0, U1=0D0, TDELTA=1D-1, TOL=1D-2
TYPE(D_OPTIONS) IOPT(3)
! Start loop to integrate and record solution values.
IDO=1
DO
SELECT CASE (IDO)
! Define values that determine limits and options.
CASE (1)
T0=ZERO
TOUT=DELTA_T
U(NPDE+1,1)=ZERO;U(NPDE+1,N)=XMAX
OPEN(FILE='PDE_ex02.out',UNIT=7)
NFRAMES=NINT((TEND+DELTA_T)/DELTA_T)
WRITE(7, "(3I5, 4D14.5)") NPDE, N, NFRAMES,&
U(NPDE+1,1), U(NPDE+1,N), T0, TEND
DX1=XMAX/N2;DX2=DX1/N1
IOPT(1)=D_OPTIONS(PDE_1D_MG_RELATIVE_TOLERANCE,ZERO)
IOPT(2)=D_OPTIONS(PDE_1D_MG_ABSOLUTE_TOLERANCE,TOL)
IOPT(3)=D_OPTIONS(PDE_1D_MG_TIME_SMOOTHING,1D-3)
! Update to the next output point.
! Write solution and check for final point.
CASE (2)
T0=TOUT
IF(T0 <= TEND) THEN
WRITE(7,"(F10.5)")TOUT
DO I=1,NPDE+1
WRITE(7,"(4E15.5)")U(I,:)
END DO
TOUT=MIN(TOUT+DELTA_T,TEND)
IF(T0 == TEND)IDO=3
END IF
! All completed. Solver is shut down.
CASE (3)
CLOSE(UNIT=7)
EXIT
! Define initial data values.
CASE (5)
U(:NPDE,:)=ZERO;U(1,:)=ONE
DO I=1,N1
U(NPDE+1,I)=(I-1)*DX2
END DO
DO I=N1+1,N
U(NPDE+1,I)=(I-N1)*DX1
END DO
WRITE(7,"(F10.5)")T0
DO I=1,NPDE+1
WRITE(7,"(4E15.5)")U(I,:)
END DO
! Define differential equations.
CASE (6)
D_PDE_1D_MG_C=ZERO
D_PDE_1D_MG_C(1,1)=ONE
D_PDE_1D_MG_C(2,1)=D_PDE_1D_MG_U(1)
D_PDE_1D_MG_R(1)=-D_PDE_1D_MG_U(2)
D_PDE_1D_MG_R(2)= D_PDE_1D_MG_DUDX(1)
D_PDE_1D_MG_Q(1)= ZERO
D_PDE_1D_MG_Q(2)= &
D_PDE_1D_MG_U(2)*D_PDE_1D_MG_DUDX(1)
! Define boundary conditions.
CASE (7)
D_PDE_1D_MG_BETA=ZERO
IF(PDE_1D_MG_LEFT) THEN
DIF=EXP(-20D0*D_PDE_1D_MG_T)
! Blend the left boundary value down to zero.
D_PDE_1D_MG_GAMMA=(/D_PDE_1D_MG_U(1)-DIF,D_PDE_1D_MG_U(2)/)
ELSE
D_PDE_1D_MG_GAMMA=(/D_PDE_1D_MG_U(1)-ONE,D_PDE_1D_MG_DUDX(2)/)
END IF
END SELECT
! Reverse communication is used for the problem data.
CALL PDE_1D_MG (T0, TOUT, IDO, U, IOPT=IOPT)
END DO
end program
Example 3 - Population Dynamics
This example is from Pennington and Berzins (1994). The system is
This is a notable problem because it involves the unknown
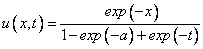across the entire
domain. The software can solve the problem by introducing two dependent
algebraic equations:
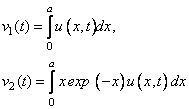
This leads to the modified system
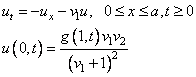
In the interface to the evaluation of the differential
equation and boundary conditions, it is necessary to evaluate the integrals,
which are computed with the values of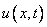 
on the grid. The integrals are approximated using the
trapezoid rule, commensurate with the truncation error in the integrator.
Rationale: Example 3
This is a non-linear integro-differential problem involving
non-local conditions for the differential equation and boundary
conditions. Access to evaluation of these conditions is provided using
reverse communication. It is not possible to solve this problem with
forward communication, given the current subroutine interface. Optional
changes are made to use an absolute error tolerance and non-zero
time-smoothing. The time-smoothing value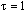
prevents grid lines from
crossing.
program PDE_1D_MG_EX03
! Population Dynamics Model.
USE PDE_1d_mg_int
USE ERROR_OPTION_PACKET
IMPLICIT NONE
INTEGER, PARAMETER :: NPDE=1, N=101
INTEGER IDO, I, NFRAMES
! Define array space for the solution.
real(kind(1d0)) U(NPDE+1,N), MID(N-1), T0, TOUT, V_1, V_2
real(kind(1d0)) :: ZERO=0D0, HALF=5D-1, ONE=1D0,&
TWO=2D0, FOUR=4D0, DELTA_T=1D-1,TEND=5D0, A=5D0
TYPE(D_OPTIONS) IOPT(3)
! Start loop to integrate and record solution values.
IDO=1
DO
SELECT CASE (IDO)
! Define values that determine limits.
CASE (1)
T0=ZERO
TOUT=DELTA_T
U(NPDE+1,1)=ZERO;U(NPDE+1,N)=A
OPEN(FILE='PDE_ex03.out',UNIT=7)
NFRAMES=NINT((TEND+DELTA_T)/DELTA_T)
WRITE(7, "(3I5, 4D14.5)") NPDE, N, NFRAMES,&
U(NPDE+1,1), U(NPDE+1,N), T0, TEND
IOPT(1)=D_OPTIONS(PDE_1D_MG_RELATIVE_TOLERANCE,ZERO)
IOPT(2)=D_OPTIONS(PDE_1D_MG_ABSOLUTE_TOLERANCE,1D-2)
IOPT(3)=D_OPTIONS(PDE_1D_MG_TIME_SMOOTHING,1D0)
! Update to the next output point.
! Write solution and check for final point.
CASE (2)
T0=TOUT
IF(T0 <= TEND) THEN
WRITE(7,"(F10.5)")TOUT
DO I=1,NPDE+1
WRITE(7,"(4E15.5)")U(I,:)
END DO
TOUT=MIN(TOUT+DELTA_T,TEND)
IF(T0 == TEND)IDO=3
END IF
! All completed. Solver is shut down.
CASE (3)
CLOSE(UNIT=7)
EXIT
! Define initial data values.
CASE (5)
U(1,:)=EXP(-U(2,:))/(TWO-EXP(-A))
WRITE(7,"(F10.5)")T0
DO I=1,NPDE+1
WRITE(7,"(4E15.5)")U(I,:)
END DO
! Define differential equations.
CASE (6)
D_PDE_1D_MG_C(1,1)=ONE
D_PDE_1D_MG_R(1)=-D_PDE_1D_MG_U(1)
! Evaluate the approximate integral, for this t.
V_1=HALF*SUM((U(1,1:N-1)+U(1,2:N))*&
(U(2,2:N) - U(2,1:N-1)))
D_PDE_1D_MG_Q(1)=V_1*D_PDE_1D_MG_U(1)
! Define boundary conditions.
CASE (7)
IF(PDE_1D_MG_LEFT) THEN
! Evaluate the approximate integral, for this t.
! A second integral is needed at the edge.
V_1=HALF*SUM((U(1,1:N-1)+U(1,2:N))*&
(U(2,2:N) - U(2,1:N-1)))
MID=HALF*(U(2,2:N)+U(2,1:N-1))
V_2=HALF*SUM(MID*EXP(-MID)*&
(U(1,1:N-1)+U(1,2:N))*(U(2,2:N)-U(2,1:N-1)))
D_PDE_1D_MG_BETA=ZERO
D_PDE_1D_MG_GAMMA=G(ONE,D_PDE_1D_MG_T)*V_1*V_2/(V_1+ONE)**2-&
D_PDE_1D_MG_U
ELSE
D_PDE_1D_MG_BETA=ZERO
D_PDE_1D_MG_GAMMA=D_PDE_1D_MG_DUDX(1)
END IF
END SELECT
! Reverse communication is used for the problem data.
CALL PDE_1D_MG (T0, TOUT, IDO, U, IOPT=IOPT)
END DO
CONTAINS
FUNCTION G(z,t)
IMPLICIT NONE
REAL(KIND(1d0)) Z, T, G
G=FOUR*Z*(TWO-TWO*EXP(-A)+EXP(-T))**2
G=G/((ONE-EXP(-A))*(ONE-(ONE+TWO*A)*&
EXP(-TWO*A))*(1-EXP(-A)+EXP(-T)))
END FUNCTION
end program
Example 4 - A Model in Cylindrical Coordinates
This example is from Blom and Zegeling (1994). The system models a reactor-diffusion problem:
The axial direction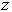 
is treated as a time coordinate. The radius 
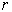is treated as the single
space variable.
Rationale: Example 4
This is a non-linear problem in cylindrical coordinates.
Our example illustrates assigning 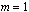in Equation 2. We provide an optional argument that
resets this value from its default, 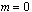. Reverse communication is used to interface with the
problem data.
! Reactor-Diffusion problem in cylindrical coordinates.
INTEGER, PARAMETER :: NPDE=1, N=41
! Define array space for the solution.
real(kind(1d0)) T(NPDE+1,N), Z0, ZOUT
real(kind(1d0)) :: ZERO=0D0, ONE=1D0, DELTA_Z=1D-1,&
ZEND=1D0, ZMAX=1D0, BTA=1D-4, GAMA=1D0, EPS=1D-1
! Start loop to integrate and record solution values.
! Define values that determine limits.
T(NPDE+1,1)=ZERO;T(NPDE+1,N)=ZMAX
OPEN(FILE='PDE_ex04.out',UNIT=7)
NFRAMES=NINT((ZEND+DELTA_Z)/DELTA_Z)
WRITE(7, "(3I5, 4D14.5)") NPDE, N, NFRAMES,&
T(NPDE+1,1), T(NPDE+1,N), Z0, ZEND
IOPT(1)=PDE_1D_MG_CYL_COORDINATES
! Update to the next output point.
! Write solution and check for final point.
! All completed. Solver is shut down.
! Define differential equations.
D_PDE_1D_MG_R(1)=BTA*D_PDE_1D_MG_DUDX(1)
D_PDE_1D_MG_Q(1)= -GAMA*EXP(D_PDE_1D_MG_U(1)/&
D_PDE_1D_MG_BETA=ONE; D_PDE_1D_MG_GAMMA=ZERO
D_PDE_1D_MG_BETA=ZERO; D_PDE_1D_MG_GAMMA=D_PDE_1D_MG_U(1)
! Reverse communication is used for the problem data.
! The optional derived type changes the internal model
! to use cylindrical coordinates.
CALL PDE_1D_MG (Z0, ZOUT, IDO, T, IOPT=IOPT)
Example 5 - A Flame Propagation Model
This example is presented more fully in Verwer, et
al., (1989). The system is a normalized problem relating mass density
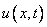and temperature
:
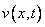Rationale: Example 5
This is a non-linear problem. The example shows the model steps for replacing the banded solver in the software with one of the user's choice. Reverse communication is used for the interface to the problem data and the linear solver. Following the computation of the matrix factorization in DL2CRB, we declare the system to be singular when the reciprocal of the condition number is smaller than the working precision. This choice is not suitable for all problems. Attention must be given to detecting a singularity when this option is used.
USE Numerical_Libraries, ONLY :&
INTEGER, PARAMETER :: NPDE=2, N=40, NEQ=(NPDE+1)*N
INTEGER I, IDO, NFRAMES, IPVT(NEQ)
! Define array space for the solution.
real(kind(1d0)) U(NPDE+1,N), T0, TOUT
! Define work space for the banded solver.
real(kind(1d0)) WORK(NEQ), RCOND
real(kind(1d0)) :: ZERO=0D0, ONE=1D0, DELTA_T=1D-4,&
TEND=6D-3, XMAX=1D0, BTA=4D0, GAMA=3.52D6
! Start loop to integrate and record solution values.
! Define values that determine limits.
U(NPDE+1,1)=ZERO; U(NPDE+1,N)=XMAX
OPEN(FILE='PDE_ex05.out',UNIT=7)
NFRAMES=NINT((TEND+DELTA_T)/DELTA_T)
WRITE(7, "(3I5, 4D14.5)") NPDE, N, NFRAMES,&
U(NPDE+1,1), U(NPDE+1,N), T0, TEND
IOPT(1)=PDE_1D_MG_REV_COMM_FACTOR_SOLVE
! Update to the next output point.
! Write solution and check for final point.
! All completed. Solver is shut down.
! Define differential equations.
D_PDE_1D_MG_C(1,1)=ONE; D_PDE_1D_MG_C(2,2)=ONE
D_PDE_1D_MG_R=D_PDE_1D_MG_DUDX
D_PDE_1D_MG_Q(1)= D_PDE_1D_MG_U(1)*F(D_PDE_1D_MG_U(2))
D_PDE_1D_MG_Q(2)= -D_PDE_1D_MG_Q(1)
D_PDE_1D_MG_BETA=ZERO;D_PDE_1D_MG_GAMMA=D_PDE_1D_MG_DUDX
IF(D_PDE_1D_MG_T >= 2D-4) THEN
D_PDE_1D_MG_GAMMA(2)=2D-1+5D3*D_PDE_1D_MG_T
D_PDE_1D_MG_GAMMA(2)=D_PDE_1D_MG_GAMMA(2)-&
! Factor the banded matrix. This is the same solver used
! internally but that is not required. A user can substitute
call dl2crb (neq, d_pde_1d_mg_a, pde_1d_mg_lda,
&
pde_1d_mg_iband, pde_1d_mg_iband, d_pde_1d_mg_a,
&
pde_1d_mg_lda, ipvt, rcond, work)
IF(rcond <= EPSILON(ONE)) pde_1d_mg_panic_flag = 1
! Solve using the factored banded matrix.
call dlfsrb(neq, d_pde_1d_mg_a, pde_1d_mg_lda,
&
pde_1d_mg_iband, pde_1d_mg_iband, ipvt,
&
d_pde_1d_mg_rhs, 1, d_pde_1d_mg_sol)
! Reverse communication is used for the problem data.
CALL PDE_1D_MG (T0, TOUT, IDO, U, IOPT=IOPT)
Example 6 - A ‘Hot Spot' Model
This example is presented more fully in Verwer, et
al., (1989). The system is a normalized problem relating the
temperature 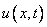, of a
reactant in a chemical system. The formula for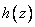 
is equivalent to their
example.
Rationale: Example 6
This is a non-linear problem. The output shows a case where a rapidly changing front, or hot-spot, develops after a considerable way into the integration. This causes rapid change to the grid. An option sets the maximum order BDF formula from its default value of 2 to the theoretical stable maximum value of 5.
INTEGER, PARAMETER :: NPDE=1, N=80
! Define array space for the solution.
real(kind(1d0)) U(NPDE+1,N), T0, TOUT
real(kind(1d0)) :: ZERO=0D0, ONE=1D0, DELTA_T=1D-2,&
TEND=29D-2, XMAX=1D0, A=1D0, DELTA=2D1, R=5D0
! Start loop to integrate and record solution values.
! Define values that determine limits.
U(NPDE+1,1)=ZERO; U(NPDE+1,N)=XMAX
OPEN(FILE='PDE_ex06.out',UNIT=7)
NFRAMES=(TEND+DELTA_T)/DELTA_T
WRITE(7, "(3I5, 4D14.5)") NPDE, N, NFRAMES,&
U(NPDE+1,1), U(NPDE+1,N), T0, TEND
! Illustrate allowing the BDF order to increase
! to its maximum allowed value.
IOPT(1)=PDE_1D_MG_MAX_BDF_ORDER
! Update to the next output point.
! Write solution and check for final point.
! All completed. Solver is shut down.
! Define differential equations.
D_PDE_1D_MG_R=D_PDE_1D_MG_DUDX
D_PDE_1D_MG_Q= - H(D_PDE_1D_MG_U(1))
D_PDE_1D_MG_GAMMA=D_PDE_1D_MG_DUDX
D_PDE_1D_MG_GAMMA=D_PDE_1D_MG_U(1)-ONE
! Reverse communication is used for the problem data.
CALL PDE_1D_MG (T0, TOUT, IDO, U, IOPT=IOPT)
H=(R/(A*DELTA))*(ONE+A-Z)*EXP(-DELTA*(ONE/Z-ONE))
Example 7 - Traveling Waves
This example is presented more fully in Verwer, et
al., (1989). The system is a normalized problem relating the
interaction of two waves, 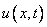and 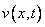moving in opposite directions. The waves meet and
reduce in amplitude, due to the non-linear terms in the equation. Then
they separate and travel onward, with reduced amplitude.
Rationale: Example 7
This is a non-linear system of first order equations.
INTEGER, PARAMETER :: NPDE=2, N=50
! Define array space for the solution.
real(kind(1d0)) U(NPDE+1,N), TEMP(N), T0, TOUT
real(kind(1d0)) :: ZERO=0D0, HALF=5D-1, &
ONE=1D0, DELTA_T=5D-2,TEND=5D-1, PI
! Start loop to integrate and record solution values.
! Define values that determine limits.
U(NPDE+1,1)=-HALF; U(NPDE+1,N)=HALF
OPEN(FILE='PDE_ex07.out',UNIT=7)
NFRAMES=(TEND+DELTA_T)/DELTA_T
WRITE(7, "(3I5, 4D14.5)") NPDE, N, NFRAMES,&
U(NPDE+1,1), U(NPDE+1,N), T0, TEND
IOPT(1)=D_OPTIONS(PDE_1D_MG_TIME_SMOOTHING,1D-3)
IOPT(2)=D_OPTIONS(PDE_1D_MG_RELATIVE_TOLERANCE,ZERO)
IOPT(3)=D_OPTIONS(PDE_1D_MG_ABSOLUTE_TOLERANCE,1D-3)
IOPT(4)=PDE_1D_MG_MAX_BDF_ORDER
! Update to the next output point.
! Write solution and check for final point.
! All completed. Solver is shut down.
U(1,:)=PULSE(TEMP); U(2,:)=U(1,:)
WHERE (TEMP < -3D-1 .or. TEMP > -1D-1) U(1,:)=ZERO
WHERE (TEMP < 1D-1 .or. TEMP > 3D-1) U(2,:)=ZERO
! Define differential equations.
D_PDE_1D_MG_C(1,1)=ONE; D_PDE_1D_MG_C(2,2)=ONE
D_PDE_1D_MG_R(1)=-D_PDE_1D_MG_R(1)
D_PDE_1D_MG_Q(1)= 100D0*D_PDE_1D_MG_U(1)*D_PDE_1D_MG_U(2)
D_PDE_1D_MG_Q(2)= D_PDE_1D_MG_Q(1)
D_PDE_1D_MG_BETA=ZERO;D_PDE_1D_MG_GAMMA=D_PDE_1D_MG_U
! Reverse communication is used for the problem data.
CALL PDE_1D_MG (T0, TOUT, IDO, U, IOPT=IOPT)
real(kind(1d0)) Z(:), PULSE(SIZE(Z))
PULSE=HALF*(ONE+COS(10D0*PI*Z))
Example 8 - Black-Scholes
The value of a European “call option,”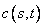 
, with exercise price 
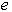and expiration date 
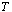, satisfies the “asset-or-nothing
payoff ”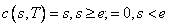 
. Prior
to expiration 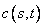is
estimated by the Black-Scholes differential equation
.
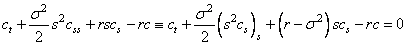The parameters in the model are the risk-free interest
rate, 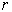, and the stock
volatility,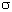
. The
boundary conditions are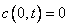 
and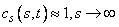 
. This development is described in Wilmott, et al.
(1995), pages 41-57. There are explicit solutions for this equation based
on the Normal Curve of Probability. The normal curve, and the solution
itself, can be efficiently computed with the IMSL function ANORDF,
IMSL (1994), page 186. With numerical integrationthe equation itself or
the payoff can be readily changed to include other formulas,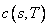 
, and corresponding boundary
conditions. We use
.
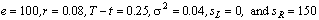Rationale: Example 8
This is a linear problem but with initial conditions that
are discontinuous. It is necessary to use a positive time-smoothing value
to prevent grid lines from crossing. We have used an absolute tolerance of
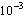. In $US, this is
one-tenth of a cent.
program PDE_1D_MG_EX08
! Black-Scholes call price
USE pde_1d_mg_int
USE error_option_packet
IMPLICIT NONE
INTEGER, PARAMETER :: NPDE=1, N=100
INTEGER I, IDO, NFRAMES
! Define array space for the solution.
real(kind(1d0)) U(NPDE+1,N), T0, TOUT, SIGSQ, XVAL
real(kind(1d0)) :: ZERO=0D0, HALF=5D-1, ONE=1D0, &
DELTA_T=25D-3, TEND=25D-2, XMAX=150, SIGMA=2D-1, &
R=8D-2, E=100D0
TYPE(D_OPTIONS) IOPT(5)
! Start loop to integrate and record solution values.
IDO=1
DO
SELECT CASE (IDO)
! Define values that determine limits.
CASE (1)
T0=ZERO
TOUT=DELTA_T
U(NPDE+1,1)=ZERO; U(NPDE+1,N)=XMAX
OPEN(FILE='PDE_ex08.out',UNIT=7)
NFRAMES=NINT((TEND+DELTA_T)/DELTA_T)
WRITE(7, "(3I5, 4D14.5)") NPDE, N, NFRAMES,&
U(NPDE+1,1), U(NPDE+1,N), T0, TEND
SIGSQ=SIGMA**2
! Illustrate allowing the BDF order to increase
! to its maximum allowed value.
IOPT(1)=PDE_1D_MG_MAX_BDF_ORDER
IOPT(2)=5
IOPT(3)=D_OPTIONS(PDE_1D_MG_TIME_SMOOTHING,5D-3)
IOPT(4)=D_OPTIONS(PDE_1D_MG_RELATIVE_TOLERANCE,ZERO)
IOPT(5)=D_OPTIONS(PDE_1D_MG_ABSOLUTE_TOLERANCE,1D-2)
! Update to the next output point.
! Write solution and check for final point.
CASE (2)
T0=TOUT
IF(T0 <= TEND) THEN
WRITE(7,"(F10.5)")TOUT
DO I=1,NPDE+1
WRITE(7,"(4E15.5)")U(I,:)
END DO
TOUT=MIN(TOUT+DELTA_T,TEND)
IF(T0 == TEND)IDO=3
END IF
! All completed. Solver is shut down.
CASE (3)
CLOSE(UNIT=7)
EXIT
! Define initial data values.
CASE (5)
U(1,:)=MAX(U(NPDE+1,:)-E,ZERO) ! Vanilla European Call
U(1,:)=U(NPDE+1,:) ! Asset-or-nothing Call
WHERE(U(1,:) <= E) U(1,:)=ZERO ! on these two lines
WRITE(7,"(F10.5)")T0
DO I=1,NPDE+1
WRITE(7,"(4E15.5)")U(I,:)
END DO
! Define differential equations.
CASE (6)
XVAL=D_PDE_1D_MG_X
D_PDE_1D_MG_C=ONE
D_PDE_1D_MG_R=D_PDE_1D_MG_DUDX*XVAL**2*SIGSQ*HALF
D_PDE_1D_MG_Q=-(R-SIGSQ)*XVAL*D_PDE_1D_MG_DUDX+R*D_PDE_1D_MG_U
! Define boundary conditions.
CASE (7)
IF(PDE_1D_MG_LEFT) THEN
D_PDE_1D_MG_BETA=ZERO
D_PDE_1D_MG_GAMMA=D_PDE_1D_MG_U
ELSE
D_PDE_1D_MG_BETA=ZERO
D_PDE_1D_MG_GAMMA=D_PDE_1D_MG_DUDX(1)-ONE
END IF
END SELECT
! Reverse communication is used for the problem data.
CALL PDE_1D_MG (T0, TOUT, IDO, U, IOPT=IOPT)
END DO
end program
Example 9 - Electrodynamics, Parameters Studied with MPI
For a detailed description of MPI Requirements see “Dense Matrix Parallelism Using MPI” in Chapter 10 of this manual.
This example, described above in Example 1, is from Blom
and Zegeling (1994). The system parameters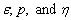 
, are varied, using uniform
random numbers. The intervals studied are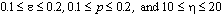 
. Using 
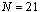grid values and other
program options, the elapsed time, parameter values, and the value 
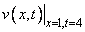are sent to the root
node. This information is written on a file. The final summary
includes the minimum value of
,
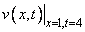and the maximum and average time per integration, per node.
Rationale: Example 9
This is a non-linear simulation problem. Using at least two integrating processors and MPI allows more values of the parameters to be studied in a given time than with a single processor. This code is valuable as a study guide when an application needs to estimate timing and other output parameters. The simulation time is controlled at the root node. An integration is started, after receiving results, within the first SIM_TIME seconds. The elapsed time will be longer than SIM_TIME by the slowest processor's time for its last integration.
program PDE_1D_MG_EX09
! Electrodynamics Model, parameter study.
USE PDE_1d_mg_int
USE MPI_SETUP_INT
USE RAND_INT
USE SHOW_INT
IMPLICIT NONE
INCLUDE "mpif.h"
INTEGER, PARAMETER :: NPDE=2, N=21
INTEGER I, IDO, IERROR, CONTINUE, STATUS(MPI_STATUS_SIZE)
INTEGER, ALLOCATABLE :: COUNTS(:)
! Define array space for the solution.
real(kind(1d0)) :: U(NPDE+1,N), T0, TOUT
real(kind(1d0)) :: ZERO=0D0, ONE=1D0,DELTA_T=10D0, TEND=4D0
! SIM_TIME is the number of seconds to run the simulation.
real(kind(1d0)) :: EPS, P, ETA, Z, TWO=2D0, THREE=3D0, SIM_TIME=60D0
real(kind(1d0)) ::
TIMES, TIMEE, TIMEL, TIME, TIME_SIM, V_MIN,
&
DATA(5)
real(kind(1d0)), ALLOCATABLE :: AV_TIME(:), MAX_TIME(:)
TYPE(D_OPTIONS) IOPT(4), SHOW_IOPT(2)
TYPE(S_OPTIONS) SHOW_INTOPT(2)
MP_NPROCS=MP_SETUP(1)
MPI_NODE_PRIORITY=(/(I-1,I=1,MP_NPROCS)/)
! If NP_NPROCS=1, the program stops. Change
! MPI_ROOT_WORKS=.TRUE. if MP_NPROCS=1.
MPI_ROOT_WORKS=.FALSE.
IF(.NOT. MPI_ROOT_WORKS .and. MP_NPROCS == 1) STOP
ALLOCATE(AV_TIME(MP_NPROCS), MAX_TIME(MP_NPROCS), COUNTS(MP_NPROCS))
! Get time start for simulation timing.
TIME=MPI_WTIME()
IF(MP_RANK == 0) OPEN(FILE='PDE_ex09.out',UNIT=7)
SIMULATE: DO
! Pick random parameter values.
EPS=1D-1*(ONE+rand(EPS))
P=1D-1*(ONE+rand(P))
ETA=10D0*(ONE+rand(ETA))
! Start loop to integrate and communicate solution times.
IDO=1
! Get time start for each new problem.
DO
IF(.NOT. MPI_ROOT_WORKS .and. MP_RANK == 0) EXIT
SELECT CASE (IDO)
! Define values that determine limits.
CASE (1)
T0=ZERO
TOUT=1D-3
U(NPDE+1,1)=ZERO;U(NPDE+1,N)=ONE
IOPT(1)=PDE_1D_MG_MAX_BDF_ORDER
IOPT(2)=5
IOPT(3)=D_OPTIONS(PDE_1D_MG_RELATIVE_TOLERANCE,1D-2)
IOPT(4)=D_OPTIONS(PDE_1D_MG_ABSOLUTE_TOLERANCE,1D-2)
TIMES=MPI_WTIME()
! Update to the next output point.
! Write solution and check for final point.
CASE (2)
T0=TOUT;TOUT=TOUT*DELTA_T
IF(T0 >= TEND) IDO=3
TOUT=MIN(TOUT, TEND)
! All completed. Solver is shut down.
CASE (3)
TIMEE=MPI_WTIME()
EXIT
! Define initial data values.
CASE (5)
U(1,:)=1D0;U(2,:)=0D0
! Define differential equations.
CASE (6)
D_PDE_1D_MG_C=0D0;D_PDE_1D_MG_C(1,1)=1D0;D_PDE_1D_MG_C(2,2)=1D0
D_PDE_1D_MG_R=P*D_PDE_1D_MG_DUDX
D_PDE_1D_MG_R(1)=D_PDE_1D_MG_R(1)*EPS
Z=ETA*(D_PDE_1D_MG_U(1)-D_PDE_1D_MG_U(2))/THREE
D_PDE_1D_MG_Q(1)=EXP(Z)-EXP(-TWO*Z)
D_PDE_1D_MG_Q(2)=-D_PDE_1D_MG_Q(1)
! Define boundary conditions.
CASE (7)
IF(PDE_1D_MG_LEFT) THEN
D_PDE_1D_MG_BETA(1)=1D0;D_PDE_1D_MG_BETA(2)=0D0
D_PDE_1D_MG_GAMMA(1)=0D0;D_PDE_1D_MG_GAMMA(2)=D_PDE_1D_MG_U(2)
ELSE
D_PDE_1D_MG_BETA(1)=0D0;D_PDE_1D_MG_BETA(2)=1D0
D_PDE_1D_MG_GAMMA(1)=D_PDE_1D_MG_U(1)-
&
1D0;D_PDE_1D_MG_GAMMA(2)=0D0
END IF
END SELECT
! Reverse communication is used for the problem data.
CALL PDE_1D_MG (T0, TOUT, IDO, U)
END DO
TIMEL=TIMEE-TIMES
DATA=(/EPS, P, ETA, U(2,N), TIMEL/)
IF(MP_RANK > 0) THEN
! Send parameters and time to the root.
CALL MPI_SEND(DATA,
5, MPI_DOUBLE_PRECISION,0, MP_RANK,
&
MP_LIBRARY_WORLD, IERROR)
! Receive back a "go/stop" flag.
CALL MPI_RECV(CONTINUE, 1, MPI_INTEGER, 0, MPI_ANY_TAG,
&
MP_LIBRARY_WORLD, STATUS, IERROR)
! If root notes that time is up, it sends node a quit flag.
IF(CONTINUE == 0) EXIT SIMULATE
ELSE
! If root is working, record its result and then stand ready
! for other nodes to send.
IF(MPI_ROOT_WORKS) WRITE(7,*) MP_RANK, DATA
! If all nodes have reported, then quit.
IF(COUNT(MPI_NODE_PRIORITY >= 0) == 0) EXIT SIMULATE
! See if time is up. Some nodes still must report.
IF(MPI_WTIME()-TIME >= SIM_TIME) THEN
CONTINUE=0
ELSE
CONTINUE=1
END IF
! Root receives simulation data and finds which node sent it.
IF(MP_NPROCS > 1) THEN
CALL MPI_RECV(DATA, 5, MPI_DOUBLE_PRECISION,
&
MPI_ANY_SOURCE, MPI_ANY_TAG, MP_LIBRARY_WORLD,
&
STATUS, IERROR)
WRITE(7,*) STATUS(MPI_SOURCE), DATA
! If time at the root has elapsed, nodes receive signal to stop.
! Send the reporting node the "go/stop" flag.
! Mark if a node has been stopped.
CALL MPI_SEND(CONTINUE, 1, MPI_INTEGER,
&
STATUS(MPI_SOURCE), &0, MP_LIBRARY_WORLD, IERROR)
IF (CONTINUE == 0)
MPI_NODE_PRIORITY(STATUS(MPI_SOURCE)+1)&
=- MPI_NODE_PRIORITY(STATUS(MPI_SOURCE)+1)-1
END IF
IF (CONTINUE == 0) MPI_NODE_PRIORITY(1)=-1
END IF
END DO SIMULATE
IF(MP_RANK == 0) THEN
ENDFILE(UNIT=7);REWIND(UNIT=7)
! Read the data. Find extremes and averages.
MAX_TIME=ZERO;AV_TIME=ZERO;COUNTS=0;V_MIN=HUGE(ONE)
DO
READ(7,*, END=10) I, DATA
COUNTS(I+1)=COUNTS(I+1)+1
AV_TIME(I+1)=AV_TIME(I+1)+DATA(5)
IF(MAX_TIME(I+1) < DATA(5)) MAX_TIME(I+1)=DATA(5)
V_MIN=MIN(V_MIN, DATA(4))
END DO
10 CONTINUE
CLOSE(UNIT=7)
! Set printing Index to match node numbering.
SHOW_IOPT(1)= SHOW_STARTING_INDEX_IS
SHOW_IOPT(2)=0
SHOW_INTOPT(1)=SHOW_STARTING_INDEX_IS
SHOW_INTOPT(2)=0
CALL SHOW(MAX_TIME,"Maximum Integration Time, per process:",IOPT=SHOW_IOPT)
AV_TIME=AV_TIME/MAX(1,COUNTS)
CALL SHOW(AV_TIME,"Average Integration Time, per process:",IOPT=SHOW_IOPT)
CALL SHOW(COUNTS,"Number of Integrations",IOPT=SHOW_INTOPT)
WRITE(*,"(1x,A,F6.3)") "Minimum value for v(x,t),at x=1,t=4: ",V_MIN
END IF
MP_NPROCS=MP_SETUP("Final")
end program
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |