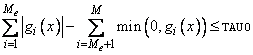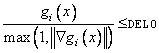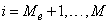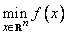Solves a general nonlinear programming problem using a sequential equality constrained quadratic programming method with user supplied gradients.
Required Arguments
FCN
User-supplied subroutine to evaluate the objective function and constraints at a
given point. The internal usage is CALL FCN (X, IACT, RESULT, IERR),
where
X The point at which the objective function or constraint is evaluated. (Input)
IACT Integer indicating whether evaluation of the objective function is requested or evaluation of a constraint is requested. If IACT is zero, then an objective function evaluation is requested. If IACT is nonzero then the value if IACT indicates the index of the constraint to evaluate. (Input)
RESULT If IACT is zero, then RESULT is the computed objective function value at the point X. If IACT is nonzero, then RESULT is the computed constraint value at the point X. (Output)
IERR Logical variable. On input IERR is set to .FALSE. If an error or other undesirable condition occurs during evaluation, then IERR should be set to .TRUE. Setting IERR to .TRUE. will result in the step size being reduced and the step being tried again. (If IERR is set to .TRUE. for XGUESS, then an error is issued.)
The routine FCN must be use-associated in a user module that uses NNLPG_INT, or else declared EXTERNAL in the calling program. If FCN is a separately compiled routine, not in a module, then it must be declared EXTERNAL.
GRAD User-supplied subroutine to evaluate the gradients at a given point. The usage is CALL GRAD (X, IACT, RESULT), where
X The point at which the gradient of the objective function or gradient of a constraint is evaluated. (Input)
IACT Integer indicating whether evaluation of the function gradient is requested or evaluation of a constraint gradient is requested. If IACT is zero, then an objective function gradient evaluation is requested. If IACT is nonzero then the value if IACT indicates the index of the constraint gradient to evaluate. (Input)RESULT If IACT is zero, then RESULT is the computed gradient of the objective function at the point X. If IACT is nonzero, then RESULT is the computed gradient of the requested constraint value at the point X. (Output)
The routine GRAD must be use-associated in a user module that uses NNLPG_INT, or else declared EXTERNAL in the calling program. If GRAD is a separately compiled routine, not in a module, then is must be declared EXTERNAL
M Total number of constraints. (Input)
ME Number of equality constraints. (Input)
IBTYPE Scalar indicating the types of bounds on variables. (Input)
0 User will supply all the bounds.
1 All variables are nonnegative.
2 All variables are nonpositive.
3 User supplies only the bounds on 1st variable, all other variables will have the same bounds.
XLB Vector of
length N containing the lower
bounds on the variables. (Input, if
IBTYPE = 0; output, if
IBTYPE = 1 or 2;
input/output, if IBTYPE = 3) If there
is no lower bound on a variable, then the corresponding XLB value should be
set to
-huge(x(1)).
XUB Vector of
length N containing the upper
bounds on the variables. (Input, if
IBTYPE = 0; output, if
IBTYPE = 1 or 2;
input/output, if IBTYPE = 3) If there
is no upper bound on a variable, then the corresponding XUB value should be
set to huge(x(1)).
X Vector of length N containing the computed solution. (Output)
Optional Arguments
N Number of
variables. (Input)
Default: N = size(X).
IPRINT Parameter indicating the desired output level. (Input)
1 One line of intermediate results is printed in each iteration.
2 Lines of intermediate results summarizing the most important data for each step are printed.
3 Lines of detailed intermediate results showing all primal and dual variables, the relevant values from the working set, progress in the backtracking and etc are printed
4 Lines of detailed intermediate results showing all primal and dual variables, the relevant values from the working set, progress in the backtracking, the gradients in the working set, the quasi-Newton updated and etc are printed.
MAXITN Maximum
number of iterations allowed. (Input)
Default: MAXITN = 200.
XGUESS Vector
of length N containing an
initial guess of the solution. (Input)
Default: XGUESS = x, (with the
smallest value of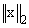 
)
that satisfies the bounds.
TAU0 A
universal bound describing how much the unscaled penalty-term may deviate from
zero. (Input)
NNLPG assumes that
within the region described by
all functions may be evaluated
safely. The initial guess however, may violate these requirements. In that case
an initial feasibility improvement phase is run by NNLPG until such a
point is found. A small TAU0 diminishes the
efficiency of NNLPG, because the
iterates then will follow the boundary of the feasible set closely. Conversely,
a large TAU0 may degrade the
reliability of the code.
Default: TAU0 = 1.E0
DEL0 In the initial phase of minimization a constraint is considered binding if
Good values are between .01 and
1.0. If DEL0 is chosen too small then
identification of the correct set of binding constraints may be delayed.
Contrary, if DEL0 is too large, then the method
will often escape to the full regularized SQP method, using individual slack
variables for any active constraint, which is quite costly. For well-scaled
problems DEL0=1.0 is reasonable.
(Input)
Default: DEL0 = .5*TAU0
SMALLW Scalar
containing the error allowed in the multipliers. For example, a negative
multiplier of an inequality constraint is accepted (as zero) if its absolute
value is less than SMALLW.
(Input)
Default: SMALLW =
exp(2*log(epsilon(x(1)/3)))
DELMIN Scalar
which defines allowable constraint violations of the final accepted
result. Constraints are satisfied if |gi(x)|
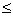DELMIN , and gj(x)
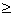(-DELMIN ) respectively. (Input)
Default:
DELMIN
= min(DEL0/10, max(1.E-6*DEL0, SMALLW))
SCFMAX Scalar
containing the bound for the internal automatic scaling of the objective
function. (Intput)
Default: SCFMAX = 1.0E4
FVALUE Scalar containing the value of the objective function at the computed solution. (Output)
FORTRAN 90 Interface
Generic: CALL NNLPG (FCN, GRAD, M, ME, IBTYPE, XLB, XUB, X [, ])
Specific: The specific interface names are S_NNLPG and D_NNLPG.
Description
The routine NNLPG provides an interface to a licensed version of subroutine DONLP2, a FORTRAN code developed by Peter Spellucci (1998). It uses a sequential equality constrained quadratic programming method with an active set technique, and an alternative usage of a fully regularized mixed constrained subproblem in case of nonregular constraints (i.e. linear dependent gradients in the working sets). It uses a slightly modified version of the Pantoja-Mayne update for the Hessian of the Lagrangian, variable dual scaling and an improved Armjijo-type stepsize algorithm. Bounds on the variables are treated in a gradient-projection like fashion. Details may be found in the following two papers:
P. Spellucci: An SQP method for general nonlinear programs using only equality constrained subproblems. Math. Prog. 82, (1998), 413-448.
P. Spellucci: A new technique for inconsistent problems in the SQP method. Math. Meth. of Oper. Res. 47, (1998), 355-500. (published by Physica Verlag, Heidelberg, Germany).
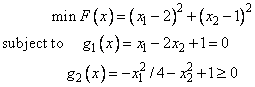
The problem is stated as follows:
Although default values are provided for optional input arguments, it may be necessary to adjust these values for some problems. Through the use of optional arguments, NNLPG allows for several parameters of the algorithm to be adjusted to account for specific characteristics of problems. The DONLP2 Users Guide provides detailed descriptions of these parameters as well as strategies for maximizing the perfomance of the algorithm. The DONLP2 Users Guide is available in the help subdirectory of the main IMSL product installation directory. In addition, the following are a number of guidelines to consider when using NNLPG.
A good initial starting point is very problem specific and should be provided by the calling program whenever possible. See optional argument XGUESS.
If a
two sided constraint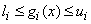 
is
transformed into two constraints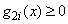 
and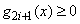 
, then choose 
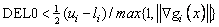, or at least try to provide an estimate for that value.
This will increase the efficiency of the algorithm. See optional
argument DEL0.
The parameter IERR provided in the interface to the user supplied function FCN can be very useful in cases when evaluation is requested at a point that is not possible or reasonable. For example, if evaluation at the requested point would result in a floating point exception, then setting IERR to .TRUE. and returning without performing the evaluation will avoid the exception. NNLPG will then reduce the stepsize and try the step again. Note, if IERR is set to .TRUE. for the initial guess, then an error is issued.
Comments
4 1 Constraint evaluation returns an error with current point.
4 2 Objective evaluation returns an error with current point.
4 3 Working set is singular in dual extended QP.
4 4 QP problem is seemingly infeasible.
4 5 A stationary point located.
4 6 A stationary point located or termination criteria too strong.
4 7 Maximum number of iterations exceeded.
4 8 Stationary point not feasible.
4 9 Very slow primal progress.
4 11 Matrix of gradients of binding constraints is singular or very ill-conditioned.
4 12 Small changes in the penalty function.
Example 1
PARAMETER (IBTYPE=0, M=2, ME=1)
REAL(KIND(1E0)) FVALUE, X(2), XGUESS(2), XLB(2), XUB(2)
CALL NNLPG (FCN, GRAD, M, ME, IBTYPE, XLB, XUB, X)
CALL WRRRN ('The solution is', X)
SUBROUTINE FCN (X, IACT, RESULT, IERR)
RESULT = (X(1)-2.0E0)**2 + (X(2)-1.0E0)**2
RESULT = X(1) - 2.0E0*X(2) + 1.0E0
RESULT = -(X(1)**2)/4.0E0 - X(2)**2 + 1.0E0
SUBROUTINE GRAD (X, IACT, RESULT)
REAL(KIND(1E0)) X(*),RESULT(*)
RESULT (1) = 2.0E0*(X(1)-2.0E0)
RESULT (2) = 2.0E0*(X(2)-1.0E0)
Output
The solution is
1
0.8229
2 0.9114
Additional Examples
Example 2
The same problem from Example 1 is solved, but here we use central differences to compute the gradient of the first constraint. This example demonstrates how NNLPG can be used in cases when analytic gradients are known for only a portion of the constraints and/or objective function. The subroutine CDGRD is used to compute an approximation to the gradient of the first constraint.
PARAMETER (IBTYPE=0, M=2, ME=1)
REAL(KIND(1E0)) FVALUE, X(2), XGUESS(2), XLB(2), XUB(2)
CALL NNLPG (FCN, GRAD, M, ME, IBTYPE, XLB, XUB, X)
CALL WRRRN ('The solution is', X)
SUBROUTINE FCN (X, IACT, RESULT, IERR)
RESULT = (X(1)-2.0E0)**2 + (X(2)-1.0E0)**2
RESULT = -(X(1)**2)/4.0E0 - X(2)**2 + 1.0E0
SUBROUTINE GRAD (X, IACT, RESULT)
REAL(KIND(1E0)) X(2),RESULT(2)
RESULT (1) = 2.0E0*(X(1)-2.0E0)
RESULT (2) = 2.0E0*(X(2)-1.0E0)
CALL CDGRD(CONSTR1, X, RESULT)
SUBROUTINE CONSTR1 (N, X, RESULT)
RESULT = X(1) - 2.0E0*X(2) + 1.0E0
Output
The solution is
1
0.8229
2 0.9114
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |