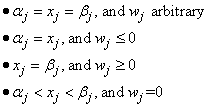For a detailed description of MPI Requirements see Dense Matrix Parallelism Using MPI in Chapter 10 of this manual.
Solves a linear least-squares system with bounds on the unknowns.
Usage Notes
CALL PARALLEL_BOUNDED_LSQ & (A, B, BND, X, RNORM, W, INDEX, IPART, & NSETP, NSETZ, IOPT=IOPT)
Required Arguments
A(1:M,:) (Input/Output) Columns of the
matrix with limits given by entries in the array IPART(1:2,1:max(1,MP_NPROCS)).
On output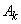 
is
replaced by the product 
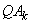, where 
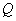is an orthogonal matrix. The value SIZE(A,1) defines the
value of M. Each
processor starts and exits with its piece of the partitioned matrix.
B(1:M) (Input/Output) Assumed-size
array of length M containing the
right-hand side vector,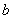 
. On output 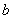is replaced by the product 
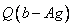, where 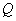is the orthogonal matrix applied
to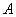
and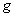 
is a set of active bounds
for the solution. All processors in the communicator start and exit with
the same vector.
BND(1:2,1:N) (Input) Assumed-size
array containing the bounds for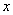 
. The lower bound 
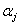is in BND(1,J), and the
upper bound 
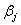is in
BND(2,J).
X(1:N) (Output) Assumed-size array of
length N containing the
solution,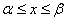 
. The
value SIZE(X) defines the
value of N. All
processors exit with the same vector.
RNORM (Output) Scalar that contains the
Euclidean or least-squares length of the residual vector,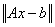 
. All processors exit with
the same value.
W(1:N) (Output) Assumed-size array of
length N containing the dual
vector,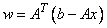 
. At a
solution exactly one of the following is true for each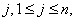 
All processors exit with the same vector.
INDEX(1:N) (Output) Assumed-size array of length N containing the NSETP indices of columns in the solution interior to bounds, and the remainder that are at a constraint. All processors exit with the same array.
IPART(1:2,1:max(1,MP_NPROCS)) (Input)
Assumed-size array containing the partitioning describing the matrix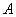. The value MP_NPROCS is the
number of processors in the communicator, except when MPI has been finalized
with a call to the routine MP_SETUP(Final').
This causes MP_NPROCS to be
assigned 0. Normally users will give the partitioning to processor
of rank = MP_RANK by setting IPART(1,MP_RANK+1)=
first column index, and IPART(2,MP_RANK+1)=
last column index. The number of columns per node is
typically based on their relative computing power. To avoid a node with
rank MP_RANK doing any work
except communication, set IPART(1,MP_RANK+1) = 0
and IPART(2,MP_RANK+1)=
-1. In this exceptional case there is no reference to the array
A(:,:) at that node.
NSETP (Output) An INTEGER indicating the number of solution components not at constraints. The column indices are output in the array INDEX(:).
NSETZ (Output) An INTEGER indicating the solution components held at fixed values. The column indices are output in the array INDEX(:).
Optional Argument
IOPT(:) (Input) Assumed-size array of derived type S_OPTIONS or D_OPTIONS. This argument is used to change internal parameters of the algorithm. Normally users will not be concerned about this argument, so they would not include it in the argument list for the routine.
IOPT(IO)=?_OPTIONS(PBLSQ_SET_TOLERANCE, TOLERANCE) Replaces the default rank tolerance for using a column, from EPSILON(TOLERANCE) to TOLERANCE. Increasing the value of TOLERANCE will cause fewer columns to be increased from their constraints, and may cause the minimum residual RNORM to increase.
IOPT(IO)=?_OPTIONS(PBLSQ_SET_MIN_RESIDUAL, RESID) Replaces the default target for the minimum residual vector length from 0 to RESID. Increasing the value of RESID can result in fewer iterations and thus increased efficiency. The descent in the optimization will stop at the first point where the minimum residual RNORM is smaller than RESID. Using this option may result in the dual vector not satisfying its optimality conditions, as noted above.
IOPT(IO)= PBLSQ_SET_MAX_ITERATIONS
IOPT(IO+1)= NEW_MAX_ITERATIONS Replaces the default maximum number of iterations from 3*N to NEW_MAX_ITERATIONS. Note that this option requires two entries in the derived type array.
FORTRAN 90 Interface
Generic: CALL PARALLEL_BOUNDED_LSQ (A, B, X [, ])
Specific: The specific interface names are S_PARALLEL_BOUNDED_LSQ and D_PARALLEL_BOUNDED_LSQ.
Description
Subroutine PARALLEL_BOUNDED_LSQ
solves the least-squares linear system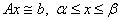 
, using the algorithm BVLS
found in Lawson and Hanson, (1995), pages 279-283. The new steps involve
updating the dual vector and exchange of required data, using MPI. The
optional changes to default tolerances, minimum residual, and the number of
iterations are new features.
Example 1: Distributed Equality and Inequality Constraint Solver
The program PBLSQ_EX1
illustrates the computation of the minimum Euclidean length
solution of an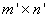 
system of linear inequality constraints , 
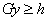. Additionally the first
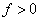of the
constraints are equalities. The solution algorithm is based on Algorithm
LDP, page 165-166, loc. cit. By allowing the dual variables
to be free, the constraints become equalities. The rows of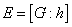 
are partitioned and assigned
random values. When the minimum Euclidean length solution to the
inequalities has been calculated, the residuals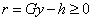 
are computed, with the dual
variables to the BVLS problem indicating the entries of
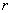that are exactly
zero.
! Use Parallel_bounded_LSQ to solve an inequality
! constraint problem, Gy >= h. Force F of the constraints
! to be equalities. This algorithm uses LDP of
! Solving Least Squares Problems, page 165.
! Forcing equality constraints by freeing the dual is
! new here. The constraints are allocated to the
! processors, by rows, in columns of the array A(:,:).
INTEGER, PARAMETER :: MP=500, NP=400, M=NP+1, &
REAL(KIND(1D0)), PARAMETER :: ZERO=0D0, ONE=1D0
REAL(KIND(1D0)), ALLOCATABLE :: &
A(:,:), B(:), BND(:,:), X(:), Y(:), &
INTEGER, ALLOCATABLE :: INDEX(:), IPART(:,:)
INTEGER K, L, DN, J, JSHIFT, IERROR, NSETP, NSETZ
DN=N/max(1,max(1,MP_NPROCS))-1
ALLOCATE(IPART(2,max(1,MP_NPROCS)))
! Spread constraint rows evenly to the processors.
! Define the constraints using random data.
K=max(0,IPART(2,MP_RANK+1)-IPART(1,MP_RANK+1)+1)
ALLOCATE(A(M,K), ASAVE(M,K), BND(2,N), &
X(N), W(N), B(M), Y(M), INDEX(N))
! The use of ASAVE can be replaced by regenerating the
! data for A(:,:) after the return from
IF(MP_RANK == 0 .and. PRINT) &
"Partition of the constraints to be solved")
! Set the right-hand side to be one in the last
! Solve the dual problem. Letting the dual variable
! have no constraint forces an equality constraint
BND(1,1:F)=-HUGE(ONE); BND(1,F+1:)=ZERO
(A, B, BND, X, RNORM, W, INDEX, IPART, &
! Each processor multiplies its block times the part
! of the dual corresponding to that partition.
DO J=IPART(1,MP_RANK+1),IPART(2,MP_RANK+1)
! Accumulate the pieces from all the processors.
! Put sum into B(:) on rank 0 processor.
CALL MPI_REDUCE(Y, B, M, MPI_DOUBLE_PRECISION,&
MPI_SUM, 0, MP_LIBRARY_WORLD, IERROR)
! Compute constraint solution at the root.
! The constraints will have no solution if B(M) = ONE.
! All of these example problems have solutions.
! Send the inequality constraint or primal solution to all nodes.
CALL MPI_BCAST(B, M, MPI_DOUBLE_PRECISION, 0, &
! For large problems this printing may need to be removed.
IF(MP_RANK == 0 .and. PRINT) &
"Minimal length solution of the constraints")
! Compute residuals of the individual constraints.
DO J=IPART(1,MP_RANK+1),IPART(2,MP_RANK+1)
X(J)=dot_product(B,ASAVE(:,JSHIFT))
! This cleans up residuals that are about rounding error
! unit (times) the size of the constraint equation and
! right-hand side. They are replaced by exact zero.
! Each group of residuals is disjoint, per processor.
! We add all the pieces together for the total set of
CALL MPI_REDUCE(X, W, N, MPI_DOUBLE_PRECISION, &
MPI_SUM, 0, MP_LIBRARY_WORLD, IERROR)
IF(MP_RANK == 0 .and. PRINT) &
call show(W, "Residuals for the constraints")
! See to any errors and shut down MPI.
IF(COUNT(W < ZERO) == 0 .and.&
COUNT(W == ZERO) >= F) WRITE(*,*)&
" Example 1 for PARALLEL_BOUNDED_LSQ is correct."
Output
Example 1 for PARALLEL_BOUNDED_LSQ is correct.
Additional Examples
Example 2: Distributed Newton-Raphson Method with Step Control
The program PBLSQ_EX2
illustrates the
computation of the solution of a non-linear system of equations. We use a
constrained Newton-Raphson method.
This algorithm works with the
problem chosen for illustration. The step-size control used here,
employing only simple bounds, may not work on other non-linear systems of
equations. Therefore we do not recommend the simple non-linear solving
technique illustrated here for an arbitrary problem. The test case
is Brown's Almost Linear Problem, Morι, et al. (1982). The
components are given by:
The functions are zero at the point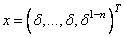
, where 
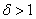is a particular root of the
polynomial equation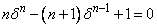 
. To avoid convergence to the local minimum 
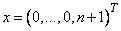, we start at the standard point
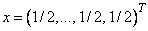and develop the Newton
method using the linear terms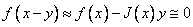 
, where 
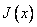is the Jacobian matrix. The update is constrained so that
the first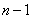 
components satisfy 
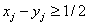, or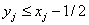 
. The last component is
bounded from both sides,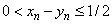 
, or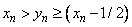 
. These bounds avoid the local minimum and allow us to
replace the last equation by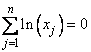 
, which is better scaled than the original. The
positive lower bound for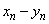 
is replaced by the strict bound, EPSILON(1D0),
the arithmetic precision, which restricts the relative accuracy of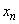 
. The input for routine PARALLEL_BOUNDED_LSQ
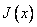expects each processor to obtain that part of it owns. Those
columns of the Jacobian matrix correspond to the partition given in the array IPART(:,:).
Here the columns of the matrix are evaluated, in parallel, on the nodes where
they are required.
! Use Parallel_bounded_LSQ to solve a non-linear system
! of equations. The example is an ACM-TOMS test problem,
! except for the larger size. It is "Brown's Almost Linear
USE Numerical_Libraries, ONLY : N1RTY
INTEGER, PARAMETER :: N=200, MAXIT=5
REAL(KIND(1D0)), PARAMETER :: ZERO=0D0, ONE=1D0,&
REAL(KIND(1D0)), ALLOCATABLE :: &
A(:,:), B(:), BND(:,:), X(:), Y(:), W(:)
INTEGER, ALLOCATABLE :: INDEX(:), IPART(:,:)
INTEGER K, L, DN, J, JSHIFT, IERROR, NSETP, &
DN=N/max(1,max(1,MP_NPROCS))-1
ALLOCATE(IPART(2,max(1,MP_NPROCS)))
! Spread Jacobian matrix columns evenly to the processors.
K=max(0,IPART(2,MP_RANK+1)-IPART(1,MP_RANK+1)+1)
X(N), W(N), B(N), Y(N), INDEX(N))
! This is Newton's method on "Brown's almost
! Turn off messages and stopping for FATAL class errors.
! Set bounds for the values after the step is taken.
! All variables are positive and bounded below by HALF,
! except for variable N, which has an upper bound of HALF.
! Compute the residual function.
B(1:N-1)=SUM(X)+X(1:N-1)-(N+1)
if(mp_rank == 0 .and. PRINT) THEN
"Developing non-linear function residual")
IF (MAXVAL(ABS(B(1:N-1))) <= SQRT(EPSILON(ONE)))&
! Compute the derivatives local to each processor.
IF(J < IPART(1,MP_RANK+1)) CYCLE
IF(J > IPART(2,MP_RANK+1)) CYCLE
A(N,:)=ONE/X(IPART(1,MP_RANK+1):IPART(2,MP_RANK+1))
! Reset the linear independence tolerance.
IOPT(1)=D_OPTIONS(PBLSQ_SET_TOLERANCE,&
IOPT(2)=PBLSQ_SET_MAX_ITERATIONS
! If N iterations was not enough on a previous iteration, reset to 2*N.
(A, B, BND, Y, RNORM, W, INDEX, IPART, NSETP, &
! The array Y(:) contains the constrained Newton step.
IF(mp_rank == 0 .and. PRINT) THEN
CALL show(BND, "Bounds for the moves")
CALL SHOW(X, "Developing Solution")
"Linear problem residual norm")
! This is a safety measure for not taking too many steps.
IF(ITER > MAXIT) EXIT NEWTON_METHOD
" Example 2 for PARALLEL_BOUNDED_LSQ is correct."
! See to any errors and shut down MPI.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |