This function evaluates a function defined on a rectangular three-dimensional grid using quadratic interpolation.

Function Return Value

QD3VL — Value of the function at (X, Y, Z).   (Output)

Required Arguments

X — x-coordinate of the point at which the function is to be evaluated.   (Input)

Y — y-coordinate of the point at which the function is to be evaluated.   (Input)

Z — z-coordinate of the point at which the function is to be evaluated.   (Input)

XDATA — Array of length NXDATA containing the location of the data points in the
x-direction.   (Input)
XDATA must be increasing.

YDATA — Array of length NYDATA containing the location of the data points in the
y-direction.   (Input)
YDATA must be increasing.

ZDATA — Array of length NZDATA containing the location of the data points in the
z-direction.   (Input)
ZDATA must be increasing.

FDATA — Array of size NXDATA by NYDATA by NZDATA containing function values.   (Input)
FDATA(I, J, K) is the value of the function at (XDATA(I), YDATA(J), ZDATA(K)).

Optional Arguments

NXDATA — Number of data points in the x-direction.   (Input)
NXDATA must be at least three.
Default: NXDATA = size (XDATA,1).

NYDATA — Number of data points in the y-direction.   (Input)
NYDATA must be at least three.
Default: NYDATA = size (YDATA,1).

NZDATA — Number of data points in the z-direction.   (Input)
NZDATA must be at least three.
Default: NZDATA = size (ZDATA,1).

LDF — Leading dimension of FDATA exactly as specified in the dimension statement of the calling program.   (Input)
LDF must be at least as large as NXDATA.
Default: LDF = size (FDATA,1).

MDF — Middle (second) dimension of FDATA exactly as specified in the dimension statement of the calling program.   (Input)
MDF must be at least as large as NYDATA.
Default: MDF = size (FDATA,2).

CHECK — Logical variable that is .TRUE. if checking of XDATA, YDATA, and ZDATA is required or .FALSE. if checking is not required.   (Input)
Default: CHECK = .TRUE.

FORTRAN 90 Interface

Generic:          QD3VL (X, Y, Z, XDATA, YDATA, ZDATA, FDATA [,…])

Specific:         The specific interface names are S_QD3VL and D_QD3VL.

FORTRAN 77 Interface

Single:     QD3VL(X, Y, Z, NXDATA, XDATA, NYDATA, YDATA, NZDATA, ZDATA, FDATA, LDF, MDF, CHECK)

Double:          The double precision function name is DQD3VL.

Description

The function QD3VL interpolates a table of values, using quadratic polynomials, returning an approximation to the tabulated function. Let (xi, yj, zk, fijk) for i = 1, …, nx, j = 1, …, ny, and
k = 1, …, nz be the tabular data. Given a point (x, y, z) at which an interpolated value is desired, we first find the nearest interior grid point (xi, yj, zk,). A trivariate quadratic interpolant q is then formed. Ten points are needed for this purpose. Seven points have the form

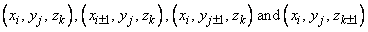
The last three points are drawn from the vertices of the octant containing (x, y, z). There are four of these vertices remaining, and we choose to exclude the vertex farthest from the center. This has the slightly deleterious effect of not reproducing the tabular data at the eight exterior corners of the table. The value q(x, y, z) is returned by QD3VL.

Comments

Informational errors

Type   Code

4           9                  The XDATA values must be strictly increasing.

4           10                The YDATA values must be strictly increasing.

4           11                The ZDATA values must be strictly increasing.

Example

In this example, the value of sin(x + y + z) at x = y = z = π/3 is approximated by using QD3VL on a grid of size 21 × 42 × 18 equally spaced values on the cube [0, 2]3.

 

      USE IMSL_LIBRARIES

 

      IMPLICIT   NONE

      INTEGER    LDF, MDF, NXDATA, NYDATA, NZDATA

      PARAMETER  (NXDATA=21, NYDATA=42, NZDATA=18, LDF=NXDATA,&

                 MDF=NYDATA)

!

      INTEGER    I, J, K, NOUT

      REAL       F, FDATA(LDF,MDF,NZDATA), FLOAT, PI, Q, &

                 SIN, X, XDATA(NXDATA), Y, YDATA(NYDATA), Z,&

                 ZDATA(NZDATA)

      INTRINSIC  FLOAT, SIN

!                                  Define function

      F(X,Y,Z) = SIN(X+Y+Z)

!                                  Set up X-grid

      DO 10  I=1, NXDATA

         XDATA(I) = 2.0*(FLOAT(I-1)/FLOAT(NXDATA-1))

   10 CONTINUE

!                                  Set up Y-grid

      DO 20  J=1, NYDATA

         YDATA(J) = 2.0*(FLOAT(J-1)/FLOAT(NYDATA-1))

   20 CONTINUE

!                                  Set up Z-grid

      DO 30  K=1, NZDATA

         ZDATA(K) = 2.0*(FLOAT(K-1)/FLOAT(NZDATA-1))

   30 CONTINUE

!                                  Evaluate function on grid

      DO 40  I=1, NXDATA

         DO 40  J=1, NYDATA

            DO 40  K=1, NZDATA

               FDATA(I,J,K) = F(XDATA(I),YDATA(J),ZDATA(K))

   40 CONTINUE

!                                  Get output unit number

      CALL UMACH (2, NOUT)

!                                  Write heading

      WRITE (NOUT,99999)

!                                  Get value for PI and set values

!                                  for X, Y, and Z

      PI = CONST('PI')

      X  = PI/3.0

      Y  = PI/3.0

      Z  = PI/3.0

!                                  Evaluate quadratic at (X,Y,Z)

      Q = QD3VL(X,Y,Z,XDATA,YDATA,ZDATA,FDATA)

!                                  Print results

      WRITE (NOUT,'(6F11.4)') X, Y, Z, F(X,Y,Z), Q, (Q-F(X,Y,Z))

99999 FORMAT (10X, 'X', 10X, 'Y', 10X, 'Z', 5X, 'F(X,Y,Z)', 4X,&

             'QD3VL', 6X, 'ERROR')

      END

Output

 

      X          Y          Z     F(X,Y,Z)    QD3VL      ERROR
1.0472     1.0472     1.0472     0.0000     0.0001     0.0001

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260