Integrates a function using a globally adaptive scheme based on Gauss-Kronrod rules.

Required Arguments

F — User-supplied FUNCTION to be integrated. The form is F(X), where
                                X − Independent variable.   (Input)
                                F − The function value.   (Output)
F must be declared EXTERNAL in the calling program.

A — Lower limit of integration.   (Input)

B — Upper limit of integration.   (Input)

RESULT — Estimate of the integral from A to B of F.   (Output)

Optional Arguments

ERRABS — Absolute accuracy desired.   (Input)
Default: ERRABS = 1.e-3 for single precision and 1.d-8 for double precision.

ERRREL — Relative accuracy desired.   (Input)
Default: ERRREL = 1.e-3 for single precision and 1.d-8 for double precision.

IRULE — Choice of quadrature rule.   (Input)
Default: IRULE = 2.
The Gauss-Kronrod rule is used with the following points:

                          IRULE   Points

1                                      7-15

2                                      10-21

3                                      15-31

4                                      20-41

5                                      25-51

6                                      30-61

IRULE = 2 is recommended for most functions. If the function has a peak singularity, use IRULE = 1. If the function is oscillatory, use IRULE = 6.

ERREST — Estimate of the absolute value of the error.   (Output)

FORTRAN 90 Interface

Generic:          CALL QDAG (F, A, B, RESULT [,…])

Specific:         The specific interface names are S_QDAG and D_QDAG.

FORTRAN 77 Interface

Single:            CALL QDAG (F, A, B, ERRABS, ERRREL, IRULE, RESULT, ERREST)

Double:          The double precision name is DQDAG.

Description

The routine QDAG is a general-purpose integrator that uses a globally adaptive scheme in order to reduce the absolute error. It subdivides the interval [A, B] and uses a (2k + 1)-point Gauss-Kronrod rule to estimate the integral over each subinterval. The error for each subinterval is estimated by comparison with the k-point Gauss quadrature rule. The subinterval with the largest estimated error is then bisected and the same procedure is applied to both halves. The bisection process is continued until either the error criterion is satisfied, roundoff error is detected, the subintervals become too small, or the maximum number of subintervals allowed is reached. The routine QDAG is based on the subroutine QAG by Piessens et al. (1983).

Should QDAG fail to produce acceptable results, then one of the IMSL routines QDAG* may be appropriate. These routines are documented in this chapter.

Comments

1.         Workspace may be explicitly provided, if desired, by use of Q2AG/DQ2AG. The reference is:

CALL Q2AG (F, A, B, ERRABS, ERRREL, IRULE, RESULT, ERREST, MAXSUB, NEVAL, NSUBIN, ALIST, BLIST, RLIST, ELIST, IORD)

The additional arguments are as follows:

MAXSUB — Number of subintervals allowed.   (Input)
A value of 500 is used by QDAG.

NEVAL — Number of evaluations of F.   (Output)

NSUBIN — Number of subintervals generated.   (Output)

ALIST — Array of length MAXSUB containing a list of the NSUBIN left endpoints.   (Output)

BLIST — Array of length MAXSUB containing a list of the NSUBIN right endpoints.   (Output)

RLIST — Array of length MAXSUB containing approximations to the NSUBIN integrals over the intervals defined by ALIST, BLIST.   (Output)

ELIST — Array of length MAXSUB containing the error estimates of the NSUBIN values in RLIST.   (Output)

IORD — Array of length MAXSUB.   (Output)
Let K be NSUBIN if NSUBIN.LE.(MAXSUB/2 + 2), MAXSUB + 1 − NSUBIN otherwise. The first K locations contain pointers to the error estimates over the corresponding subintervals, such that ELIST(IORD(1)), …, ELIST(IORD(K)) form a decreasing sequence.

2.         Informational errors
Type                                   Code

   4                  1       The maximum number of subintervals allowed has been reached.

   3                  2       Roundoff error, preventing the requested tolerance from being achieved, has been detected.

   3                  3       A degradation in precision has been detected.

3.         If EXACT is the exact value, QDAG attempts to find RESULT such that
ABS(EXACT − RESULT).LE.MAX(ERRABS, ERRREL * ABS(EXACT)). To specify only a relative error, set ERRABS to zero. Similarly, to specify only an absolute error, set ERRREL to zero.

Example

The value of

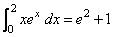
is estimated. Since the integrand is not oscillatory, IRULE = 1 is used. The values of the actual and estimated error are machine dependent.

 

      USE QDAG_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

      INTEGER    IRULE, NOUT

      REAL       A, ABS, B, ERRABS, ERREST, ERROR, EXACT, EXP, &

                 F, RESULT

      INTRINSIC  ABS, EXP

      EXTERNAL   F

!                                 Get output unit number

      CALL UMACH (2, NOUT)

!                                 Set limits of integration

      A = 0.0

      B = 2.0

!                                 Set error tolerances

      ERRABS = 0.0

!                                 Parameter for non-oscillatory

!                                 function

      IRULE = 1

      CALL QDAG (F, A, B, RESULT, ERRABS=ERRABS, IRULE=IRULE, ERREST=ERREST)

!                                 Print results

      EXACT = 1.0 + EXP(2.0)

      ERROR = ABS(RESULT-EXACT)

      WRITE (NOUT,99999) RESULT, EXACT, ERREST, ERROR

99999 FORMAT (' Computed =', F8.3, 13X, ' Exact =', F8.3, /, /, &

            ' Error estimate =', 1PE10.3, 6X, 'Error =', 1PE10.3)

      END

!

      REAL FUNCTION F (X)

      REAL       X

      REAL       EXP

      INTRINSIC  EXP

      F = X*EXP(X)

      RETURN

      END

Output

 

Computed =   8.389              Exact =   8.389

Error estimate = 5.000E-05      Error = 9.537E-07

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260