Integrates a function (which may have endpoint singularities).

Required Arguments

F — User-supplied FUNCTION to be integrated. The form is F(X), where
                                X −Independent variable.   (Input)
                                F − The function value.   (Output)
F must be declared EXTERNAL in the calling program.

A — Lower limit of integration.   (Input)

B — Upper limit of integration.   (Input)

RESULT — Estimate of the integral from A to B of F.   (Output)

Optional Required Arguments

ERRABS — Absolute accuracy desired.   (Input)
Default: ERRABS = 1.e-3 for single precision and 1.d-8 for double precision.

ERRREL — Relative accuracy desired.   (Input)
Default: ERRREL = 1.e-3 for single precision and 1.d-8 for double precision.

ERREST — Estimate of the absolute value of the error.   (Output)

FORTRAN 90 Interface

Generic:          CALL QDAGS (F, A, B, RESULT [,…])

Specific:         The specific interface names are S_QDAGS and D_QDAGS.

FORTRAN 77 Interface

Single:            CALL QDAGS (F, A, B, ERRABS, ERRREL, RESULT, ERREST)

Double:          The double precision name is DQDAGS.

Description

The routine QDAGS is a general-purpose integrator that uses a globally adaptive scheme to reduce the absolute error. It subdivides the interval [A, B] and uses a 21-point Gauss-Kronrod rule to estimate the integral over each subinterval. The error for each subinterval is estimated by comparison with the 10-point Gauss quadrature rule. This routine is designed to handle functions with endpoint singularities. However, the performance on functions, which are well-behaved at the endpoints, is quite good also. In addition to the general strategy described in QDAG, this routine uses an extrapolation procedure known as the ɛ-algorithm. The routine QDAGS is an implementation of the routine QAGS, which is fully documented by Piessens et al. (1983). Should QDAGS fail to produce acceptable results, then either IMSL routines QDAG or QDAG* may be appropriate. These routines are documented in this chapter.

Comments

1.         Workspace may be explicitly provided, if desired, by use of Q2AGS/DQ2AGS. The reference is

CALL Q2AGS (F, A, B, ERRABS, ERRREL, RESULT, ERREST, MAXSUB, NEVAL, NSUBIN, ALIST, BLIST, RLIST, ELIST, IORD)

The additional arguments are as follows:

MAXSUB — Number of subintervals allowed.   (Input)
A value of 500 is used by QDAGS.

NEVAL — Number of evaluations of F.   (Output)

NSUBIN — Number of subintervals generated.   (Output)

ALIST — Array of length MAXSUB containing a list of the NSUBIN left endpoints.   (Output)

BLIST — Array of length MAXSUB containing a list of the NSUBIN right endpoints.   (Output)

RLIST — Array of length MAXSUB containing approximations to the NSUBIN integrals over the intervals defined by ALIST, BLIST.   (Output)

ELIST — Array of length MAXSUB containing the error estimates of the NSUBIN values in RLIST.   (Output)

IORD — Array of length MAXSUB.   (Output)
Let k be
NSUBIN                                  if NSUBIN ≤ (MAXSUB/2 + 2);
MAXSUB + 1 − NSUBIN       otherwise.
The first k locations contain pointers to the error estimates over the subintervals such that ELIST(IORD(1)), …, ELIST(IORD(k)) form a decreasing sequence.

2.         Informational errors

Type   Code

4           1                  The maximum number of subintervals allowed has been reached.

3           2                  Roundoff error, preventing the requested tolerance from being achieved, has been detected.

3           3                  A degradation in precision has been detected.

3           4                  Roundoff error in the extrapolation table, preventing the requested tolerance from being achieved, has been detected.

4           5                  Integral is probably divergent or slowly convergent.

3.         If EXACT is the exact value, QDAGS attempts to find RESULT such that
|EXACT − RESULT| ≤ max(ERRABS, ERRREL * |EXACT|). To specify only a relative error, set ERRABS to zero. Similarly, to specify only an absolute error, set ERRREL to zero.

Example

The value of

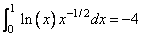
is estimated. The values of the actual and estimated error are machine dependent.

 

      USE QDAGS_INT

      USE UMACH_INT

 

      IMPLICIT NONE

      INTEGER    NOUT

      REAL       A, ABS, B, ERRABS, ERREST, ERROR, ERRREL, EXACT, F, &

                RESULT

      INTRINSIC  ABS

      EXTERNAL   F

!                                 Get output unit number

      CALL UMACH (2, NOUT)

!                                 Set limits of integration

      A = 0.0

      B = 1.0

!                                 Set error tolerances

      ERRABS = 0.0

      CALL QDAGS (F, A, B, RESULT, ERRABS=ERRABS, ERREST=ERREST)

!                                 Print results

      EXACT = -4.0

      ERROR = ABS(RESULT-EXACT)

      WRITE (NOUT,99999) RESULT, EXACT, ERREST, ERROR

99999 FORMAT (' Computed =', F8.3, 13X, ' Exact =', F8.3, /, /, &

            ' Error estimate =', 1PE10.3, 6X, 'Error =', 1PE10.3)

      END

!

      REAL FUNCTION F (X)

      REAL       X

      REAL       ALOG, SQRT

      INTRINSIC  ALOG, SQRT

      F = ALOG(X)/SQRT(X)

      RETURN

      END

Output

 

Computed =  -4.000              Exact =  -4.000

Error estimate = 1.519E-04      Error = 2.098E-05

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260