Integrates a function with algebraic-logarithmic singularities.

Required Arguments

F — User-supplied FUNCTION to be integrated. The form is F(X), where
                                X − Independent variable.   (Input)
                                F − The function value.   (Output)
F must be declared EXTERNAL in the calling program.

A — Lower limit of integration.   (Input)

B — Upper limit of integration.   (Input)
B must be greater than A

IWEIGH — Type of weight function used.   (Input)

IWEIGH                  Weight

1                              (X − A)**ALPHA * (B − X)**BETAW

2                              (X − A)**ALPHA * (B − X)**BETAW * LOG(X − A)

3                              (X − A)**ALPHA * (B − X)**BETAW * LOG(B − X)

4                              (X − A)**ALPHA * (B − X)**BETAW * LOG (X− A) * LOG (B − X)

ALPHA — Parameter in the weight function.   (Input)
ALPHA must be greater than −1.0.

BETAW — Parameter in the weight function.   (Input)
BETAW must be greater than −1.0.

RESULT — Estimate of the integral from A to B of F * WEIGHT.   (Output)

Optional Arguments

ERRABS — Absolute accuracy desired.   (Input)
Default: ERRABS = 1.e-3 for single precision and 1.d-8 for double precision.

ERRREL — Relative accuracy desired.   (Input)
Default: ERRREL = 1.e-3 for single precision and 1.d-8 for double precision.

ERREST — Estimate of the absolute value of the error.   (Output)

FORTRAN 90 Interface

Generic:          CALL QDAWS (F, A, B, IWEIGH, ALPHA, BETAW, RESULT[,…] )

Specific:         The specific interface names are S_QDAWS and D_QDAWS.

FORTRAN 77 Interface

Single:            CALL QDAWS (F, A, B, IWEIGH, ALPHA, BETAW, ERRABS, ERRREL, RESULT, ERREST)

Double:          The double precision name is DQDAWS.

Description

The routine QDAWS uses a globally adaptive scheme in an attempt to reduce the absolute error. This routine computes integrals whose integrands have the special form w(x) f(x), where w(x) is a weight function described above. A combination of modified Clenshaw-Curtis and Gauss-Kronrod formulas is employed. In addition to the general strategy described for the IMSL routine QDAG, this routine uses an extrapolation procedure known as the ɛ-algorithm. The routine QDAWS is an implementation of the routine QAWS, which is fully documented by Piessens et al. (1983).

Comments

1.         Workspace may be explicitly provided, if desired, by use of Q2AWS/DQ2AWS. The reference is

CALL Q2AWS (F, A, B, IWEIGH, ALPHA, BETAW, ERRABS, ERRREL, RESULT, ERREST, MAXSUB, NEVAL, NSUBIN, ALIST, BLIST, RLIST, ELIST, IORD)

The additional arguments are as follows:

MAXSUB — Maximum number of subintervals allowed.   (Input)
A value of 500 is used by QDAWS.

NEVAL — Number of evaluations of F.   (Output)

NSUBIN — Number of subintervals generated.   (Output)

ALIST — Array of length MAXSUB containing a list of the NSUBIN left endpoints.   (Output)

BLIST — Array of length MAXSUB containing a list of the NSUBIN right endpoints.   (Output)

RLIST — Array of length MAXSUB containing approximations to the NSUBIN integrals over the intervals defined by ALIST, BLIST.   (Output)

ELIST — Array of length MAXSUB containing the error estimates of the NSUBIN values in RLIST.   (Output)

IORD — Array of length MAXSUB. Let k be NSUBIN if NSUBIN.LE.
(MAXSUB/2 + 2), MAXSUB + 1 − NSUBIN otherwise. The first k locations contain pointers to the error estimates over the subintervals, such that ELIST(IORD(1)), …, ELIST(IORD(k)) form a decreasing sequence.   (Output)

2.         Informational errors
Type                                   Code

   4                   1      The maximum number of subintervals allowed has been reached.

   3                   2      Roundoff error, preventing the requested tolerance from being achieved, has been detected.

   3                   3      A degradation in precision has been detected.

3.         If EXACT is the exact value, QDAWS attempts to find RESULT such that
ABS(EXACT − RESULT).LE.MAX(ERRABS, ERRREL * ABS(EXACT)). To specify only a relative error, set ERRABS to zero. Similarly, to specify only an absolute error, set ERRREL to zero.

Example

The value of

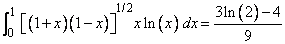
is estimated. The values of the actual and estimated error are machine dependent.

 

      USE QDAWS_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

      INTEGER    IWEIGH, NOUT

      REAL       A, ABS, ALOG, ALPHA, B, BETAW, ERRABS, ERREST, ERROR, &

                EXACT, F, RESULT

      INTRINSIC  ABS, ALOG

      EXTERNAL   F

!                                 Get output unit number

      CALL UMACH (2, NOUT)

!                                 Set limits of integration

      A = 0.0

      B = 1.0

!                                 Select weight

      ALPHA  = 1.0

      BETAW   = 0.5

      IWEIGH = 2

!                                 Set error tolerances

      ERRABS = 0.0

      CALL QDAWS (F, A, B, IWEIGH, ALPHA, BETAW, RESULT, &

                ERRABS=ERRABS, ERREST=ERREST)

!                                 Print results

      EXACT = (3.*ALOG(2.)-4.)/9.

      ERROR = ABS(RESULT-EXACT)

      WRITE (NOUT,99999) RESULT, EXACT, ERREST, ERROR

99999 FORMAT (' Computed =', F8.3, 13X, ' Exact =', F8.3, /, /, &

            ' Error estimate =', 1PE10.3, 6X, 'Error =', 1PE10.3)

      END

!

      REAL FUNCTION F (X)

      REAL       X

      REAL       SQRT

      INTRINSIC  SQRT

      F = SQRT(1.0+X)

      RETURN

      END

Output

 

Computed =  -0.213              Exact =  -0.213

Error estimate = 1.261E-08      Error = 2.980E-08

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260