Solves a quadratic programming problem subject to linear equality/inequality constraints.

Required Arguments

NEQ — The number of linear equality constraints.   (Input)

A — NCON by NVAR matrix.   (Input)
The matrix contains the equality contraints in the first NEQ rows followed by the inequality constraints.

B — Vector of length NCON containing right-hand sides of the linear constraints.   (Input)

G — Vector of length NVAR containing the coefficients of the linear term of the objective function.   (Input)

H — NVAR by NVAR matrix containing the Hessian matrix of the objective function.   (Input)
H should be symmetric positive definite; if H is not positive definite, the algorithm attempts to solve the QP problem with H replaced by a H + DIAGNL * I such that
H + DIAGNL * I is positive definite. See Comment 3.

SOL — Vector of length NVAR containing solution.   (Output)

Optional Arguments

NVAR — The number of variables.   (Input)
Default: NVAR = size (A,2).

NCON — The number of linear constraints.   (Input)
Default: NCON = size (A,1).

LDA — Leading dimension of A exactly as specified in the dimension statement of the calling program.   (Input)
Default: LDA = size (A,1).

LDH — Leading dimension of H exactly as specified in the dimension statement of the calling program.   (Input)
Default: LDH = size (H,1).

DIAGNL — Scalar equal to the multiple of the identity matrix added to H to give a positive definite matrix.   (Output)

NACT — Final number of active constraints.   (Output)

IACT — Vector of length NVAR containing the indices of the final active constraints in the first NACT positions.   (Output)

ALAMDA — Vector of length NVAR containing the Lagrange multiplier estimates of the final active constraints in the first NACT positions.   (Output)

FORTRAN 90 Interface

Generic:          CALL QPROG (NEQ, A, B, G, H, SOL [,…])

Specific:         The specific interface names are S_QPROG and D_QPROG.

FORTRAN 77 Interface

Single:            CALL QPROG (NVAR, NCON, NEQ, A, LDA, B, G, H, LDH, DIAGNL, SOL, NACT, IACT, ALAMDA)

Double:          The double precision name is DQPROG.

Description

The routine QPROG is based on M.J.D. Powell's implementation of the Goldfarb and Idnani (1983) dual quadratic programming (QP) algorithm for convex QP problems subject to general linear equality/inequality constraints, i.e., problems of the form

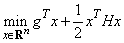
subject to         A1x = b1

                                           A1x ≥ b2

given the vectors b1, b2, and g and the matrices H, A1, and A2. H is required to be positive definite. In this case, a unique x solves the problem or the constraints are inconsistent. If H is not positive definite, a positive definite perturbation of H is used in place of H. For more details, see Powell (1983, 1985).

Comments

1.         Workspace may be explicitly provided, if desired, by use of Q2ROG/DQ2ROG. The reference is:

CALL Q2ROG (NVAR, NCON, NEQ, A, LDA, B, G, H, LDH, DIAGNL, SOL, NACT, IACT, ALAMDA, WK)

The additional argument is:

WK — Work vector of length (3 * NVAR**2 + 11 * NVAR)/2 + NCON.

2.         Informational errors

Type   Code

3           1                  Due to the effect of computer rounding error, a change in the variables fail to improve the objective function value; usually the solution is close to optimum.

4           2                  The system of equations is inconsistent. There is no solution.

3.         If a perturbation of H, H + DIAGNL * I, was used in the QP problem, then
H + DIAGNL * I should also be used in the definition of the Lagrange multipliers.

Example

The quadratic programming problem

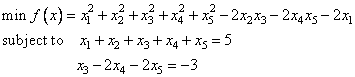
is solved.

 

      USE QPROG_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

!                                 Declare variables

      INTEGER    LDA, LDH, NCON, NEQ, NVAR

      PARAMETER  (NCON=2, NEQ=2, NVAR=5, LDA=NCON, LDH=NVAR)

!

      INTEGER    K, NACT, NOUT

      REAL       A(LDA,NVAR), ALAMDA(NVAR), B(NCON), G(NVAR), &

                H(LDH,LDH), SOL(NVAR)

!

!                                 Set values of A, B, G and H.

!                                 A = ( 1.0  1.0  1.0  1.0  1.0)

!                                     ( 0.0  0.0  1.0 -2.0 -2.0)

!

!                                 B = ( 5.0 -3.0)

!

!                                 G = (-2.0  0.0  0.0  0.0  0.0)

!

!                                 H = ( 2.0  0.0  0.0  0.0  0.0)

!                                     ( 0.0  2.0 -2.0  0.0  0.0)

!                                     ( 0.0 -2.0  2.0  0.0  0.0)

!                                     ( 0.0  0.0  0.0  2.0 -2.0)

!                                     ( 0.0  0.0  0.0 -2.0  2.0)

!

      DATA A/1.0, 0.0, 1.0, 0.0, 1.0, 1.0, 1.0, -2.0, 1.0, -2.0/

      DATA B/5.0, -3.0/

      DATA G/-2.0, 4*0.0/

      DATA H/2.0, 5*0.0, 2.0, -2.0, 3*0.0, -2.0, 2.0, 5*0.0, 2.0, &

          -2.0, 3*0.0, -2.0, 2.0/

!

      CALL QPROG (NEQ, A, B, G, H, SOL)

!

      CALL UMACH (2, NOUT)

      WRITE (NOUT,99999) (SOL(K),K=1,NVAR)

99999 FORMAT ('  The solution vector is', /, '  SOL = (', 5F6.1, &

            '  )')

!

      END

Output

 

The solution vector is
SOL = (   1.0   1.0   1.0   1.0   1.0  )

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260