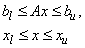Solves a sparse linear programming problem via the revised simplex algorithm.
Required Arguments
A Vector of length NZ containing the coefficients of the M constraints. (Input)
IROW Vector of length NZ containing the row numbers of the corresponding element in A. (Input)
JCOL Vector of length NZ containing the column numbers of the corresponding elements in A. (Input)
BL Vector of length M containing the lower limit of the general constraints; if there is no lower limit on the I-th constraint, then BL(I) is not referenced. (Input)
BU Vector of length M containing the upper lower limit of the general constraints; if there is no upper limit on the I-th constraint, then BU(I) is not referenced. (Input)
C Vector of length NVAR containing the coefficients of the objective function. (Input)
IRTYPE Vector
of length M indicating the types
of general constraints in the matrix A.
(Input)
Let R(I) = A(I, 1)*XSOL(1)
+
+ A(I, NVAR)*XSOL(NVAR)
IRTYPE(I)
I-th CONSTRAINT
0
BL(I) = R(I) = BU(I)
1
R(I) ≤ BU(I)
2
R(I) ≥ BL(I)
3
BL(I) ≤ R(I) ≤ BU(I)
OBJ Value of the objective function. (Output)
XSOL Vector of length NVAR containing the primal solution. (Output)
DSOL Vector of length M containing the dual solution. (Output)
Optional Arguments
M Number of
constraints. (Input)
Default: M = size
(IRTYPE,1).
NVAR Number of
variables. (Input)
Default: NVAR = size
(C,1).
NZ Number of
nonzero coefficients in the matrix A. (Input)
Default: NZ = size
(A,1).
XLB Vector of
length NVAR containing the
lower bound on the variables; if there is no lower bound on a variable, then
1.0E30 should be set as the lower bound. (Input)
Default: XLB = 0.0.
XUB Vector of
length NVAR containing the
upper bound on the variables; if there is no upper bound on a variable, then -1.0E30 should be
set as the upper bound. (Input)
Default: XLB = 3.4e38 for
single precision and 1.79d + 308 for double precision.
FORTRAN 90 Interface
Generic: CALL SLPRS (A, IROW, JCOL, BL, BU, C, IRTYPE, OBJ, XSOL, DSOL [, ])
Specific: The specific interface names are S_SLPRS and D_SLPRS.
FORTRAN 77 Interface
Single: CALL SLPRS (M, NVAR, NZ, A, IROW, JCOL, BL, BU, C, IRTYPE, XLB, XUB, OBJ, XSOL, DSOL)
Double: The double precision name is DSLPRS.
Description
This subroutine solves problems of the form
where c is the objective coefficient vector, A is the coefficient matrix, and the vectors bl, bu, xl, and xu are the lower and upper bounds on the constraints and the variables, respectively. SLPRS is designed to take advantage of sparsity in A. The routine is based on DPLO by Hanson and Hiebert.
Comments
Workspace may be explicitly
provided, if desired, by use of S2PRS/DS2PRS. The
reference is:
CALL S2PRS (M, NVAR, NZ, A, IROW, JCOL, BL, BU, C, IRTYPE, XLB, XUB, OBJ, XSOL, DSOL, IPARAM, RPARAM, COLSCL, ROWSCL, WORK, LW, IWORK, LIW)
The additional arguments are as follows:
IPARAM
Integer parameter vector of length 12. If the default parameters are desired for
SLPRS, then set IPARAM(1) to zero and call the routine SLPRS. Otherwise, if any nondefault
parameters are desired for IPARAM or RPARAM, then the following steps should be
taken before calling SLPRS:
CALL S5PRS (IPARAM, RPARAM)
Set nondefault values for IPARAM and RPARAM.
Note that the call to S5PRS will set IPARAM and RPARAM to their
default values so only nondefault values need to be set above.
IPARAM(1) = 0 indicates that a minimization problem is solved. If set to 1, a maximization problem is solved.
IPARAM(2) = switch indicating the maximum number of iterations to be taken before returning to the user. If set to zero, the maximum number of iterations taken is set to 3*(NVARS+M). If positive, that value is used as the iteration limit.
IPARAM(3) = indicator for choosing how columns are selected to enter the basis. If set to zero, the routine uses the steepest edge pricing strategy which is the best local move. If set to one, the minimum reduced cost pricing strategy is used. The steepest edge pricing strategy generally uses fewer iterations than the minimum reduced cost pricing, but each iteration costs more in terms of the amount of calculation performed. However, this is very problem-dependent.
IPARAM(4) = MXITBR, the number of iterations between recalculating the error in the primal solution is used to monitor the error in solving the linear system. This is an expensive calculation and every tenth iteration is generally enough.
IPARAM(5) = NPP, the number of
negative reduced costs (at most) to be found at each iteration of choosing a
variable to enter the basis. If set to zero,
NPP = NVARS will be used, implying that all of
the reduced costs are computed at each such step. This Partial pricing may
increase the total number of iterations required. However, it decreases the
number of calculation required at each iteration. The effect on overall
efficiency is very problem-dependent. If set to some positive number, that value
is used as NPP.
IPARAM(6) = IREDFQ, the number of steps between basis matrix redecompositions. Redecompositions also occur whenever the linear systems for the primal and dual systems have lost half their working precision.
IPARAM(7) = LAMAT, the length of the portion of WORK that is allocated to sparse matrix storage and decomposition. LAMAT must be greater than NZ + NVARS + 4.
Default: LAMAT = NZ + NVARS + 5
IPARAM(8) = LBM, then length of the portion of IWORK that is allocated to sparse matrix storage and decomposition. LBM must be positive.
IPARAM(9) = switch indicating that partial results should be saved after the maximum number of iterations, IPARAM(2), or at the optimum. If IPARAM(9) is not zero, data essential to continuing the calculation is saved to a file, attached to unit number IPARAM(9). The data saved includes all the information about the sparse matrix A and information about the current basis. If IPARAM(9) is set to zero, partial results are not saved. It is the responsibility of the calling program to open the output file.
IPARAM(10) = switch indicating that partial results have been computed and stored on unit number IPARAM(10), if greater than zero. If IPARAM(10) is zero, a new problem is started.
IPARAM(11) = switch indicating that the user supplies scale factors for the columns of the matrix A. If IPARAM(11) = 0, SLPRS computes the scale factors as the reciprocals of the max norm of each column. If IPARAM(11) is set to one, element I of the vector COLSCL is used as the scale factor for column I of the matrix A. The scaling is implicit, so no input data is actually changed.
IPARAM(12) = switch indicating that the user supplied scale factors for the rows of the matrix A. If IPARAM(12) is set to zero, no row scaling is one. If IPARAM(12) is set to 1, element I of the vector ROWSCL is used as the scale factor for row I of the matrix A. The scaling is implicit, so no input data is actually changed.
RPARAM Real parameter vector of length 7.
RPARAM(1) = COSTSC, a scale
factor for the vector of costs. Normally
SLPRS computes
this scale factor to be the reciprocal of the max norm if the vector costs after
the column scaling has been applied. If RPARAM(1) is zero,
SLPRS compute COSTSC.
RPARAM(2) = ASMALL, the smallest magnitude of nonzero entries in the matrix A. If RPARAM(2) is nonzero, checking is done to ensure that all elements of A are at least as large as RPARAM(2). Otherwise, no checking is done.
RPARAM(3) = ABIG, the largest magnitude of nonzero entries in the matrix A. If RPARAM(3) is nonzero, checking is done to ensure that all elements of A are no larger than RPARAM(3). Otherwise, no checking is done.
RPARAM(4) = TOLLS, the relative tolerance used in checking if the residuals are feasible. RPARAM(4) is nonzero, that value is used as TOLLS, otherwise the default value is used.
Default: TOLLS = 1000.0*amach(4)
RPARAM(5) = PHI, the scaling factor used to scale the reduced cost error estimates. In some environments, it may be necessary to reset PHI to the range [0.01, 0.1], particularly on machines with short word length and working precision when solving a large problem. If RPARAM(5) is nonzero, that value is used as PHI, otherwise the default value is used.
RPARAM(6) = TOLABS, an absolute error test on feasibility. Normally a relative test is used with TOLLS (see RPARAM(4)). If this test fails, an absolute test will be applied using the value TOLABS.
RPARAM(7) = pivot tolerance of the underlying sparse factorization routine. If RPARAM(7) is set to zero, the default pivot tolerance is used, otherwise, the RPARAM(7) is used.
COLSCL
Array of length NVARS containing column scale factors for
the matrix A. (Input).
COLSCL is not used
if IPARAM(11) is set to zero.
ROWSCL
Array of length M containing row scale factors for the
matrix A. (Input)
ROWSCL is not used
if IPARAM(12) is set to zero.
WORK Work array of length LW.
LW Length
of real work array. LW must be at least
2 + 2NZ + 9NVAR + 27M + MAX(NZ + NVAR + 8, 4NVAR + 7).
IWORK Integer work array of length LIW.
LIW
Length of integer work array. LIW must be at
least
1 + 3NVAR + 41M + MAX(NZ + NVAR + 8, 4NVAR + 7).
Example
Solve a linear programming problem, with
defined in sparse coordinate format.
! Specifications for local variables
INTEGER INDEX, IROW(3*M), J, JCOL(3*M), NOUT, NZ
REAL A(3*M), DSOL(M), OBJ, XSOL(NVAR)
REAL B(M), C(NVAR), XL(NVAR), XU(NVAR)
! Specifications for subroutines
DATA C/-1.0, -2.0, -3.0, -4.0, -5.0, -6.0, -7.0, -8.0, -9.0, &
CALL SLPRS (A, IROW, JCOL, B, B, C, IRTYPE, OBJ, XSOL, DSOL, &
99999 FORMAT (/, 'The value of the objective function is ', E12.6)
Output
The value of the objective function is -.280971E+03
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |