Calculates the indices of eigenvalues of a Sturm-Liouville problem of the form for

with boundary conditions (at regular points)
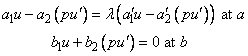
in a specified subinterval of the real line, [, ].
Required Arguments
ALPHA Value of the left end point of the search interval. (Input)
BETAR Value of the right end point of the search interval. (Input)
CONS Array of size eight containing

in locations CONS(1) CONS(8), respectively. (Input)
COEFFN
User-supplied SUBROUTINE to evaluate
the coefficient functions. The usage is
CALL COEFFN (X, PX, QX, RX)
X Independent
variable. (Input)
PX The value of
p(x) at X.
(Output)
QX
The value of
q(x) at X.
(Output)
RX
The value of
r(x) at X.
(Output)
COEFFN must be
declared EXTERNAL in the
calling program.
ENDFIN Logical array of size two. ENDFIN = .true. if and only if the endpoint a is finite. ENDFIN(2) = .true. if and only if endpoint b is finite. (Input)
IFIRST The index of the first eigenvalue greater than . (Output)
NTOTAL Total number of eigenvalues in the interval [, ]. (Output)
FORTRAN 90 Interface
Generic: CALL SLCNT (ALPHA, BETAR, CONS, COEFFN, ENDFIN, IFIRST, NTOTAL)
Specific: The specific interface names are S_SLCNT and D_SLCNT.
FORTRAN 77 Interface
Single: CALL SLCNT (ALPHA, BETAR, CONS, COEFFN, ENDFIN, IFIRST, NTOTAL)
Double: The double precision name is DSLCNT.
Description
This subroutine computes the indices of eigenvalues, if any, in a subinterval of the real line for Sturm-Liouville problems in the form

with boundary conditions (at regular points)
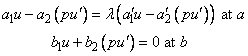
It is intended to be used in conjunction with SLEIG. SLCNT is based on the routine INTERV from the package SLEDGE.
Example
Consider the harmonic oscillator (Titchmarsh) defined by
p(x) = 1
q(x) = x2
r(x) = 1
[a, b] = [, ]
u(a) = 0
u(b) = 0
The eigenvalues of this problem are known to be
k = 2k + 1, k = 0, 1,
Therefore in the interval [10, 16] we expect SLCNT to note three eigenvalues, with the first of these having index five.
USE SLCNT_INT
USE UMACH_INT
IMPLICIT NONE
! SPECIFICATIONS FOR LOCAL VARIABLES
INTEGER IFIRST, NOUT, NTOTAL
REAL ALPHA, BETAR, CONS(8)
LOGICAL ENDFIN(2)
! SPECIFICATIONS FOR SUBROUTINES
! SPECIFICATIONS FOR FUNCTIONS
EXTERNAL COEFFN
!
CALL UMACH (2, NOUT)
! set u(a) = 0, u(b) = 0
CONS(1) = 1.0E0
CONS(2) = 0.0E0
CONS(3) = 0.0E0
CONS(4) = 0.0E0
CONS(5) = 1.0E0
CONS(6) = 0.0E0
CONS(7) = 0.0E0
CONS(8) = 0.0E0
!
ENDFIN(1) = .FALSE.
ENDFIN(2) = .FALSE.
!
ALPHA = 10.0
BETAR = 16.0
!
CALL SLCNT (ALPHA, BETAR, CONS, COEFFN, ENDFIN, IFIRST, NTOTAL)
!
WRITE (NOUT,99998) ALPHA, BETAR, IFIRST
WRITE (NOUT,99999) NTOTAL
!
99998 FORMAT (/, 'Index of first eigenvalue in [', F5.2, ',', F5.2, &
'] IS ', I2)
99999 FORMAT ('Total number of eigenvalues in this interval: ', I2)
!
END
!
SUBROUTINE COEFFN (X, PX, QX, RX)
! SPECIFICATIONS FOR ARGUMENTS
REAL X, PX, QX, RX
!
PX = 1.0E0
QX = X*X
RX = 1.0E0
RETURN
END
Output
Index of first eigenvalue in
[10.00,16.00] is 5
Total number of eigenvalues in this interval: 3
[1] The
assign-to equality, 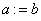 , used here
and below, is read the expression
, used here
and below, is read the expression is evaluated and then assigned to the
location
is evaluated and then assigned to the
location 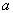 .
.
[2] The three-tiered equal sign, used here and below, is read a Ί b or a and b are exactly the same object or value.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |