Determines eigenvalues, eigenfunctions and/or spectral density functions for Sturm-Liouville problems in the form
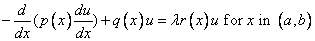
with boundary conditions (at regular points)
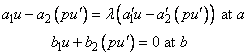
Required Arguments
CONS — Array of size eight containing
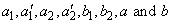
in locations CONS(1) through CONS(8), respectively. (Input)
COEFFN —
User-supplied SUBROUTINE to evaluate
the coefficient functions. The usage is
CALL COEFFN (X, PX, QX, RX)
X — Independent
variable. (Input)
PX — The value of
p(x) at X.
(Output)
QX —
The value of q(x) at X.
(Output)
RX —
The value of r(x) at X.
(Output)
COEFFN must be
declared EXTERNAL in the
calling program.
ENDFIN — Logical array of size two. ENDFIN(1) = .true. if the endpoint a is finite. ENDFIN(2) = .true. if endpoint b is finite. (Input)
INDEX — Vector of size NUMEIG containing the indices of the desired eigenvalues. (Input)
EVAL — Array of length NUMEIG containing the computed approximations to the eigenvalues whose indices are specified in INDEX. (Output)
Optional Arguments
NUMEIG — The
number of eigenvalues desired. (Input)
Default: NUMEIG = size
(INDEX,1).
TEVLAB — Absolute
error tolerance for eigenvalues. (Input)
Default: TEVLAB = 10.*
machine precision.
TEVLRL — Relative
error tolerance for eigenvalues. (Input)
Default: TEVLRL = SQRT(machine
precision).
FORTRAN 90 Interface
Generic: CALL SLEIG (CONS, COEFFN, ENDFIN, INDEX, EVAL [,…])
Specific: The specific interface names are S_SLEIG and D_SLEIG.
FORTRAN 77 Interface
Single: CALL SLEIG (CONS, COEFFN, ENDFIN, NUMEIG, INDEX, TEVLAB, TEVLRL, EVAL)
Double: The double precision name is DSLEIG.
Description
This subroutine is designed for the calculation of eigenvalues, eigenfunctions and/or spectral density functions for Sturm-Liouville problems in the form
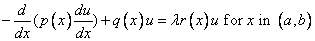 (1)
(1)
with boundary conditions (at regular points)
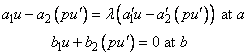
We assume that
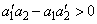
when aʹ1 0 and aʹ2 0. The problem is considered regular if and only if
a and b are finite,
p(x) and r(x) are positive in (a, b),
1/p(x), q(x) and r(x) are locally integrable near the endpoints.
Otherwise the problem is called singular. The theory assumes that p, pʹ, q, and r are at least continuous on (a, b), though a finite number of jump discontinuities can be handled by suitably defining an input mesh.
For regular problems, there are an infinite number of eigenvalues
0 < 1 < < k, k
Each eigenvalue has an associated eigenfunction which is unique up to a constant. For singular problems, there is a wide range in the behavior of the eigenvalues.
As presented in Pruess and Fulton (1993) the approach is to replace (1) by a new problem
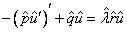 (2)
(2)
with analogous boundary conditions
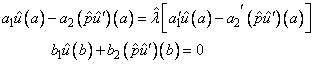
where
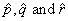
are step function approximations to p, q, and
r, respectively. Given the mesh
a = x1 <
x2 <
< xN+1 =
b, the usual choice for the step functions uses midpoint interpolation,
i. e.,
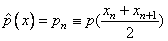
for x in (xn, xn+1) and similarly for the other coefficient functions. This choice works well for regular problems. Some singular problems require a more sophisticated technique to capture the asymptotic behavior. For the midpoint interpolants, the differential equation (2) has the known closed form solution in
(xn, xn+1)
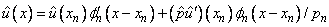
with
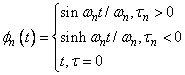
where
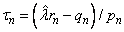
and
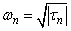
Starting with,
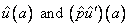
consistent with the boundary condition,
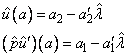
an algorithm is to compute for n = 1, 2, ..., N,
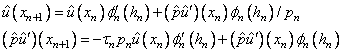
which is a shooting method. For a fixed mesh we can iterate on the approximate eigenvalue until the boundary condition at b is satisfied. This will yield an O(h2) approximation
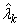
to some k.
The problem (2) has a step spectral function given by
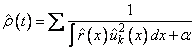
where the sum is taken over k such that
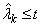
and
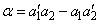
Comments
1. Workspace may be explicitly provided, if desired, by use of S2EIG/DS2EIG. The reference is:
CALL S2EIG (CONS, COEFFN, ENDFIN, NUMEIG, INDEX, TEVLAB, TEVLRL, EVAL, JOB, IPRINT, TOLS, NUMX, XEF, NRHO, T, TYPE, EF, PDEF, RHO, IFLAG, WORK, IWORK)
The additional arguments are as follows:
JOB — Logical array of length five. (Input)
JOB(1) = .true. if a set of eigenvalues are to be computed but not their eigenfunctions.
JOB(2) = .true. if a set of eigenvalue and eigenfunction pairs are to be computed.
JOB(3) = .true. if the spectral function is to be
computed
over some subinterval of the essential spectrum.
JOB(4) = .true. if the normal automatic classification is overridden. If JOB(4) = .true. then TYPE(*,*) must be entered correctly. Most users will not want to override the classification process, but it might be appropriate for users experimenting with problems for which the coefficient functions do not have power-like behavior near the singular endpoints. The classification is considered sufficiently important for spectral density function calculations that JOB(4) is ignored with JOB(3) = .true..
JOB(5) = .true. if mesh distribution is chosen by SLEIG. If JOB(5) = .true. and NUMX is zero, the number of mesh points are also chosen by SLEIG. If NUMX > 0 then NUMX mesh points will be used. If JOB(5) = .false., the number NUMX and distribution XEF(*) must be input by the user.
IPRINT — Control
levels of internal printing. (Input)
No printing is performed if
IPRINT = 0.
If either JOB(1) or JOB(2) is true:
IPRINT
Printed
Output
1
initial mesh (the first 51 or fewer points), eigenvalue estimate
at each
level
4
the above and at each level matching point for
eigenfunction shooting, X(*), EF(*) and PDEF(*)
values
5
the above and at each level the brackets for the eigenvalue
search, intermediate shooting information for the eigenfunction and
eigenfunction norm.
If JOB(3) =
.true.
IPRINT
Printed
Output
1
the actual (a, b) used at each iteration and the total number
of eigenvalues
computed
2
the above and switchover points to the asymptotic
formulas, and some intermediate (t)
approximations
4
the above and initial meshes for each iteration, the index
of the largest eigenvalue which may be computed, and various
eigenvalue and RN
values
4
the above and
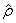
values at each
level
5
the above and RN add eigenvalues below the switchover
point
If JOB(4)=.false.
IPRINT
Printed
Output
2
output a description of the
spectrum
3
the above and the constants for the Friedrichs' boundary
condition(s)
5
the above and intermediate details of the classification
calculation
TOLS — Array of
length 4 containing tolerances. (Input)
TOLS(1) — absolute
error tolerance for eigenfunctions
TOLS(2) — relative error tolerance for
eigenfunctions
TOLS(3) — absolute error tolerance for
eigenfunction derivatives
TOLS(4) — relative error tolerance for
eigenfunction derivatives
The absolute tolerances must be positive.
The relative tolerances must be at
least 100 *amach(4)
NUMX — Integer whose value is the number of output points where each eigenfunction is to be evaluated (the number of entries in XEF(*)) when JOB(2) = .true.. If JOB(5)= .false. and NUMX is greater than zero, then NUMX is the number of points in the initial mesh used. If JOB(5) = .false., the points in XEF(*) should be chosen with a reasonable distribution. Since the endpoints a and b must be part of any mesh, NUMX cannot be one in this case. If JOB(5) = .false. and JOB(3) = .true., then NUMX must be positive. On output, NUMX is set to the number of points for eigenfunctions when input NUMX = 0, and JOB(2) or JOB(5) = .true.. (Input/Output)
XEF — Array of
points on input where eigenfunction estimates are desired, if JOB(2) = .true.. Otherwise, if JOB(5) = .false.
and NUMX is
greater than zero, the user's initial mesh is entered. The entries must be
ordered so that
a = XEF(1) < XEF(2) < < XEF(NUMX) = b.
If either endpoint is infinite, the corresponding XEF(1) or XEF(NUMX) is ignored. However, it is required
that XEF(2)
be negative when ENDFIN(1) = .false., and that XEF(NUMX-1) be
positive when
ENDFIN(2) = .false.. On output, XEF(*) is changed
only if JOB(2) and JOB(5) are true. If JOB(2) = .false.,
this vector is not referenced. If JOB(2) = .true. and NUMX is greater
than zero on input, XEF(*) should be dimensioned at least NUMX + 16. If
JOB(2) is
true and NUMX is zero on input, XEF(*) should be
dimensioned at least 31.
NRHO — The number of output values desired for the array RHO(*). NRHO is not used if JOB(3) = .false.. (Input)
T — Real vector of size NRHO containing values where the spectral function RHO(*) is desired. The entries must be sorted in increasing order. The existence and location of a continuous spectrum can be determined by calling SLEIG with the first four entries of JOB set to false and IPRINT set to 1. T(*) is not used if JOB(3) = .false.. (Input)
TYPE — 4 by 2
logical matrix. Column 1 contains information about endpoint a and column
2 refers to endpoint b.
TYPE(1,*) = .true. if and only if the
endpoint is regular
TYPE(2,*) = .true. if and only if the
endpoint is limit circle
TYPE(3,*) = .true. if and only if the
endpoint is nonoscillatory for all eigenvalues
TYPE(4,*) = .true. if and only if the
endpoint is oscillatory for all eigenvalues
Note: all of these values must be
correctly input if JOB(4) = .true..
Otherwise, TYPE(*,*) is
output. (Input/Output)
EF — Array of eigenfunction values. EF((k 1)*NUMX + i) is the estimate of u(XEF(i)) corresponding to the eigenvalue in EV(k). If JOB(2) = .false. then this vector is not referenced. If JOB(2) = .true. and NUMX is greater than zero on entry, then EF(*) should be dimensioned at least NUMX * NUMEIG. If JOB(2) = .true. and NUMX is zero on input, then EF(*) should be dimensioned 31 * NUMEIG. (Output)
PDEF — Array of eigenfunction derivative values. PDEF((k-1)*NUMX + i) is the estimate of (puʹ) (XEF(i)) corresponding to the eigenvalue in EV(k). If JOB(2) = .false. this vector is not referenced. If JOB(2) = .true., it must be dimensioned the same as EF(*). (Output)
RHO — Array of
size NRHO
containing values for the spectral density function (t),
RHO(I) = (T(I)). This vector
is not referenced if JOB(3) is false. (Output)
IFLAG — Array of
size max(1, numeig) containing information
about the output. IFLAG(K) refers to the K-th eigenvalue,
when JOB(1)
or JOB(2) =
.true.. Otherwise, only IFLAG(1) is used. Negative values are
associated with fatal errors, and the calculations are ceased. Positive values
indicate a warning. (Output)
IFLAG(K)
|
IFLAG(K) |
Description |
|
1 |
too many levels needed for the eigenvalue calculation; problem seems too difficult at this tolerance. Are the coefficient functions nonsmooth? |
|
2 |
too many levels needed for the eigenfunction calculation; problem seems too difficult at this tolerance. Are the eigenfunctions ill-conditioned? |
|
3 |
too many levels needed for the spectral density calculation; problem seems too difficult at this tolerance. |
|
4 |
the user has requested the spectral density function for a problem which has no continuous spectrum. |
|
5 |
the user has requested the spectral density function for a problem with both endpoints generating essential spectrum, i.e. both endpoints either OSC or O-NO. |
|
6 |
the user has requested the spectral density function for a problem in spectral category 2 for which a proper normalization of the solution at the NONOSC endpoint is not known; for example, problems with an irregular singular point or infinite endpoint at one end and continuous spectrum generated at the other. |
|
7 |
problems were encountered in obtaining a bracket. |
|
8 |
too small a step was used in the integration. The TOLS(*) values may be too small for this problem. |
|
9 |
too small a step was used in the spectral density function calculation for which the continuous spectrum is generated by a finite endpoint. |
|
10 |
an argument to the circular trig functions is too large. Try running the problem again with a finer initial mesh or, for singular problems, use interval truncation. |
|
15 |
p(x) and r(x) are not positive in the interval (a, b). |
|
20 |
eigenvalues and/or eigenfunctions were requested for a problem with an OSC singular endpoint. Interval truncation must be used on such problems. |
|
1 |
Failure in the bracketing procedure probably due to a cluster of eigenvalues which the code cannot separate. Calculations have continued but any eigenfunction results are suspect. Try running the problem again with tighter input tolerances to separate the cluster. |
|
2 |
there is uncertainty in the classification for this problem. Because of the limitations of floating point arithmetic, and the nature of the finite sampling, the routine cannot be certain about the classification information at the requested tolerance. |
|
3 |
there may be some eigenvalues embedded in the essential spectrum. Use of IPRINT greater than zero will provide additional output giving the location of the approximating eigenvalues for the step function problem. These could be extrapolated to estimate the actual eigenvalue embedded in the essential spectrum. |
|
4 |
a change of variables was made to avoid potentially slow convergence. However, the global error estimates may not be as reliable. Some experimentation using different tolerances is recommended. |
|
6 |
there were problems with eigenfunction convergence in a spectral density calculation. The output (t) may not be accurate. |
WORK — Array of size MAX(1000, NUMEIG + 22) used for workspace.
IWORK — Integer array of size NUMEIG + 3 used for workspace.
Example 1
This example computes the first ten eigenvalues of the problem from Titchmarsh (1962) given by
p(x) = r(x) = 1
q(x) = x
[a, b] = [0, ]
u(a) = u(b) = 0
The eigenvalues are known to be the zeros of
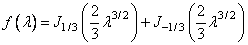
For each eigenvalue k, the program prints k, k and f(k).
USE SLEIG_INT
USE CBJS_INT
IMPLICIT NONE
! SPECIFICATIONS FOR LOCAL VARIABLES
INTEGER I, INDEX(10), NUMEIG, NOUT
REAL CONS(8), EVAL(10), LAMBDA, TEVLAB,&
TEVLRL, XNU
COMPLEX CBS1(1), CBS2(1), Z
LOGICAL ENDFIN(2)
! SPECIFICATIONS FOR INTRINSICS
INTRINSIC CMPLX, SQRT
REAL SQRT
COMPLEX CMPLX
! SPECIFICATIONS FOR SUBROUTINES
! SPECIFICATIONS FOR FUNCTIONS
EXTERNAL COEFF
!
CALL UMACH (2, NOUT)
! Define boundary conditions
CONS(1) = 1.0
CONS(2) = 0.0
CONS(3) = 0.0
CONS(4) = 0.0
CONS(5) = 1.0
CONS(6) = 0.0
CONS(7) = 0.0
CONS(8) = 0.0
!
ENDFIN(1) = .TRUE.
ENDFIN(2) = .FALSE.
! Compute the first 10 eigenvalues
NUMEIG = 10
DO 10 I=1, NUMEIG
INDEX(I) = I - 1
10 CONTINUE
! Set absolute and relative tolerance
!
CALL SLEIG (CONS, COEFF, ENDFIN, INDEX, EVAL)
!
XNU = -1.0/3.0
WRITE(NOUT,99998)
DO 20 I=1, NUMEIG
LAMBDA = EVAL(I)
Z = CMPLX(2.0/3.0*LAMBDA*SQRT(LAMBDA),0.0)
CALL CBJS (XNU, Z, 1, CBS1)
CALL CBJS (-XNU, Z, 1, CBS2)
WRITE (NOUT,99999) I-1, LAMBDA, REAL(CBS1(1) + CBS2(1))
20 CONTINUE
!
99998 FORMAT(/, 2X, 'index', 5X, 'lambda', 5X, 'f(lambda)',/)
99999 FORMAT(I5, F13.4, E15.4)
END
!
SUBROUTINE COEFF (X, PX, QX, RX)
! SPECIFICATIONS FOR ARGUMENTS
REAL X, PX, QX, RX
!
PX = 1.0
QX = X
RX = 1.0
RETURN
END
Output
index lambda f(lambda)
0
2.3381 -0.8285E-05
1 4.0879
-0.1651E-04
2
5.5205 0.6843E-04
3 6.7867
-0.4523E-05
4
7.9440 0.8952E-04
5 9.0227
0.1123E-04
6
10.0401 0.1031E-03
7 11.0084
-0.7913E-04
8
11.9361 -0.5095E-04
9 12.8293 0.4645E-03
Additional Examples
Example 2
In this problem from Scott, Shampine and Wing (1969),
p(x) = r(x) = 1
q(x) = x2 + x4
[a, b] = [, ]
u(a) = u(b) = 0
the first eigenvalue and associated eigenfunction, evaluated at selected points, are computed. As a rough check of the correctness of the results, the magnitude of the residual
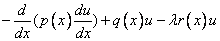
is printed. We compute a spline interpolant to uʹ and use the function CSDER to estimate the quantity (p(x)uʹ)ʹ.
USE S2EIG_INT
USE CSDER_INT
USE UMACH_INT
USE CSAKM_INT
IMPLICIT NONE
! SPECIFICATIONS FOR LOCAL VARIABLES
INTEGER I, IFLAG(1), INDEX(1), IWORK(100), NINTV, NOUT, NRHO, &
NUMEIG, NUMX
REAL BRKUP(61), CONS(8), CSCFUP(4,61), EF(61), EVAL(1), &
LAMBDA, PDEF(61), PX, QX, RESIDUAL, RHO(1), RX, T(1), &
TEVLAB, TEVLRL, TOLS(4), WORK(3000), X, XEF(61)
LOGICAL ENDFIN(2), JOB(5), TYPE(4,2)
! SPECIFICATIONS FOR INTRINSICS
INTRINSIC ABS, REAL
REAL ABS, REAL
! SPECIFICATIONS FOR SUBROUTINES
EXTERNAL COEFF
! Define boundary conditions
CONS(1) = 1.0
CONS(2) = 0.0
CONS(3) = 0.0
CONS(4) = 0.0
CONS(5) = 1.0
CONS(6) = 0.0
CONS(7) = 0.0
CONS(8) = 0.0
! Compute eigenvalue and eigenfunctions
JOB(1) = .FALSE.
JOB(2) = .TRUE.
JOB(3) = .FALSE.
JOB(4) = .FALSE.
JOB(5) = .FALSE.
!
ENDFIN(1) = .FALSE.
ENDFIN(2) = .FALSE.
! Compute eigenvalue with index 0
NUMEIG = 1
INDEX(1) = 0
!
TEVLAB = 1.0E-3
TEVLRL = 1.0E-3
TOLS(1) = TEVLAB
TOLS(2) = TEVLRL
TOLS(3) = TEVLAB
TOLS(4) = TEVLRL
NRHO = 0
! Set up mesh, points at which u and
! u' will be computed
NUMX = 61
DO 10 I=1, NUMX
XEF(I) = 0.05*REAL(I-31)
10 CONTINUE
!
CALL S2EIG (CONS, COEFF, ENDFIN, NUMEIG, INDEX, TEVLAB, TEVLRL, &
EVAL, JOB, 0, TOLS, NUMX, XEF, NRHO, T, TYPE, EF, &
PDEF, RHO, IFLAG, WORK, IWORK)
!
LAMBDA = EVAL(1)
20 CONTINUE
! Compute spline interpolant to u'
!
CALL CSAKM (XEF, PDEF, BRKUP, CSCFUP)
NINTV = NUMX - 1
!
CALL UMACH (2, NOUT)
WRITE (NOUT,99997) ' lambda = ', LAMBDA
WRITE (NOUT,99999)
! At a subset of points from the
! input mesh, compute residual =
! abs( -(u')' + q(x)u - lambda*u ).
! We know p(x) = 1 and r(x) = 1.
DO 30 I=1, 41, 2
X = XEF(I+10)
CALL COEFF (X, PX, QX, RX)
!
! Use the spline fit to u' to
! estimate u'' with CSDER
!
RESIDUAL = ABS(-CSDER(1,X,BRKUP,CSCFUP)+QX*EF(I+10)- &
LAMBDA*EF(I+10))
WRITE (NOUT,99998) X, EF(I+10), PDEF(I+10), RESIDUAL
30 CONTINUE
!
99997 FORMAT (/, A14, F10.5, /)
99998 FORMAT (5X, F4.1, 3F15.5)
99999 FORMAT (7X, 'x', 11X, 'u(x)', 10X, 'u''(x)', 9X, 'residual', /)
END
!
SUBROUTINE COEFF (X, PX, QX, RX)
! SPECIFICATIONS FOR ARGUMENTS
REAL X, PX, QX, RX
!
PX = 1.0
QX = X*X + X*X*X*X
RX = 1.0
RETURN
END
Output
lambda = 1.39247
x u(x) u'(x) residual
-1.0 0.38632 0.65019 0.00189
-0.9 0.45218 0.66372 0.00081
-0.8 0.51837 0.65653 0.00023
-0.7 0.58278 0.62827 0.00113
-0.6 0.64334 0.57977 0.00183
-0.5 0.69812 0.51283 0.00230
-0.4 0.74537 0.42990 0.00273
-0.3 0.78366 0.33393 0.00265
-0.2 0.81183 0.22811 0.00273
-0.1 0.82906 0.11570 0.00278
0.0 0.83473 0.00000 0.00136
0.1 0.82893 -0.11568 0.00273
0.2 0.81170 -0.22807 0.00273
0.3 0.78353 -0.33388 0.00267
0.4 0.74525 -0.42983 0.00265
0.5 0.69800 -0.51274 0.00230
0.6 0.64324 -0.57967 0.00182
0.7 0.58269 -0.62816 0.00113
0.8 0.51828 -0.65641 0.00023
0.9 0.45211 -0.66361 0.00081
1.0 0.38626 -0.65008 0.00189
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |