Computes a smooth bivariate interpolant to scattered data that is locally a quintic polynomial in two variables.
Required Arguments
XYDATA — A 2 by
NDATA array
containing the coordinates of the interpolation points. (Input)
These points must be distinct. The x-coordinate of the I-th data point is
stored in XYDATA(1, I) and the
y-coordinate of the I-th data point is
stored in XYDATA(2, I).
FDATA — Array of length NDATA containing the interpolation values. (Input) FDATA(I) contains the value at (XYDATA(1, I), XYDATA(2, I)).
XOUT — Array of
length NXOUT
containing an increasing sequence of points. (Input)
These
points are the x-coordinates of a grid on which the interpolated surface
is to be evaluated.
YOUT — Array of
length NYOUT
containing an increasing sequence of points. (Input)
These
points are the y-coordinates of a grid on which the interpolated surface
is to be evaluated.
SUR — Matrix of
size NXOUT by
NYOUT.
(Output)
This matrix contains the values of the surface on the XOUT by YOUT grid, i.e. SUR(I, J) contains the
interpolated value at (XOUT(I), YOUT(J)).
Optional Arguments
NDATA — Number of
data points. (Input)
NDATA must be at least
four.
Default: NDATA = size (FDATA,1).
NXOUT — The
number of elements in XOUT.
(Input)
Default: NXOUT = size (XOUT,1).
NYOUT — The
number of elements in YOUT.
(Input)
Default: NYOUT = size (YOUT,1).
LDSUR — Leading
dimension of SUR
exactly as specified in the dimension statement of the calling
program. (Input)
LDSUR must be at least
as large as NXOUT.
Default:
LDSUR = size
(SUR,1).
FORTRAN 90 Interface
Generic: CALL SURF (XYDATA, FDATA, XOUT, YOUT, SUR [,…])
Specific: The specific interface names are S_SURF and D_SURF.
FORTRAN 77 Interface
Single: CALL SURF (NDATA, XYDATA, FDATA, NXOUT, NYOUT, XOUT, YOUT, SUR, LDSUR)
Double: The double precision name is DSURF.
Description
This routine is designed to compute a C 1 interpolant to scattered data in the plane. Given the data points
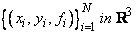
SURF returns (in SUR, the user-specified grid) the values of the interpolant s. The computation of s is as follows: First the Delaunay triangulation of the points
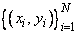
is computed. On each triangle T in this triangulation, s has the form
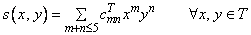
Thus, s is a bivariate quintic polynomial on each triangle of the triangulation. In addition, we have
s(xi, yi) = fi for i = 1, …, N
and s is continuously differentiable across the boundaries of neighboring triangles. These conditions do not exhaust the freedom implied by the above representation. This additional freedom is exploited in an attempt to produce an interpolant that is faithful to the global shape properties implied by the data. For more information on this routine, we refer the reader to the article by Akima (1978). The grid is specified by the two integer variables NXOUT, NYOUT that represent, respectively, the number of grid points in the first (second) variable and by two real vectors that represent, respectively, the first (second) coordinates of the grid.
Comments
1. Workspace may be explicitly provided, if desired, by use of S2RF/DS2RF. The reference is:
CALL S2RF (NDATA, XYDATA, FDATA, NXOUT, NYOUT, XOUT, YOUT, SUR, LDSUR, IWK, WK)
The additional arguments are as follows:
IWK — Work array of length 31 * NDATA + 2*(NXOUT * NYOUT).
WK — Work array of length 6 * NDATA.
2. Informational errors
Type Code
4 5 The data point values must be distinct.
4 6 The XOUT values must be strictly increasing.
4 7 The YOUT values must be strictly increasing.
3. This method of interpolation reproduces linear functions.
Example
In this example, the interpolant to the linear function 3 + 7x + 2y is computed from 20 data points equally spaced on the circle of radius 3. We then print the values on a 3 × 3 grid.
USE IMSL_LIBRARIES
IMPLICIT NONE
INTEGER LDSUR, NDATA, NXOUT, NYOUT
PARAMETER (NDATA=20, NXOUT=3, NYOUT=3, LDSUR=NXOUT)
!
INTEGER I, J, NOUT
REAL ABS, COS, F, FDATA(NDATA), FLOAT, PI,&
SIN, SUR(LDSUR,NYOUT), X, XOUT(NXOUT),&
XYDATA(2,NDATA), Y, YOUT(NYOUT)
INTRINSIC ABS, COS, FLOAT, SIN
! Define function
F(X,Y) = 3.0 + 7.0*X + 2.0*Y
! Get value for PI
PI = CONST('PI')
! Set up X, Y, and F data on a circle
DO 10 I=1, NDATA
XYDATA(1,I) = 3.0*SIN(2.0*PI*FLOAT(I-1)/FLOAT(NDATA))
XYDATA(2,I) = 3.0*COS(2.0*PI*FLOAT(I-1)/FLOAT(NDATA))
FDATA(I) = F(XYDATA(1,I),XYDATA(2,I))
10 CONTINUE
! Set up XOUT and YOUT data on [0,1] by
! [0,1] grid.
DO 20 I=1, NXOUT
XOUT(I) = FLOAT(I-1)/FLOAT(NXOUT-1)
20 CONTINUE
DO 30 I=1, NXOUT
YOUT(I) = FLOAT(I-1)/FLOAT(NYOUT-1)
30 CONTINUE
! Interpolate scattered data
CALL SURF (XYDATA, FDATA, XOUT, YOUT, SUR)
! Get output unit number
CALL UMACH (2, NOUT)
! Write heading
WRITE (NOUT,99998)
! Print results
DO 40 I=1, NYOUT
DO 40 J=1, NXOUT
WRITE (NOUT,99999) XOUT(J), YOUT(I), SUR(J,I),&
F(XOUT(J),YOUT(I)),&
ABS(SUR(J,I)-F(XOUT(J),YOUT(I)))
40 CONTINUE
99998 FORMAT (' ', 10X, 'X', 11X, 'Y', 9X, 'SURF', 6X, 'F(X,Y)', 7X,&
'ERROR', /)
99999 FORMAT (1X, 5F12.4)
END
Output
X
Y
SURF F(X,Y)
ERROR
0.0000
0.0000 3.0000
3.0000
0.0000
0.5000
0.0000 6.5000
6.5000
0.0000
1.0000 0.0000
10.0000 10.0000
0.0000
0.0000
0.5000 4.0000
4.0000
0.0000
0.5000
0.5000 7.5000
7.5000
0.0000
1.0000 0.5000
11.0000 11.0000
0.0000
0.0000
1.0000 5.0000
5.0000
0.0000
0.5000
1.0000 8.5000
8.5000
0.0000
1.0000 1.0000
12.0000 12.0000 0.0000
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |