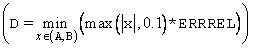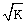ZBREN

Finds a zero of a real function that changes sign in a given interval.

Required Arguments

F — User-supplied FUNCTION to compute the value of the function of which a zero will be found. The form is F(X), where

X — The point at which the function is evaluated. (Input)
X should not be changed by F.

F — The computed function value at the point X. (Output)
F must be declared EXTERNAL in the calling program.

A — See B. (Input/Output)

B — On input, the user must supply two points, A and B, such that F(A) and F(B) are opposite in sign. (Input/Output)
On output, both A and B are altered. B will contain the best approximation to the zero of F.

Optional Arguments

ERRABS — First stopping criterion. (Input)
A zero, B, is accepted if ABS(F(B)) is less than or equal to ERRABS. ERRABS may be set to zero.
Default: ERRABS = 1.e-4 for single precision and 1.d-8 for double precision.

ERRREL — Second stopping criterion is the relative error. (Input)
A zero is accepted if the change between two successive approximations to this zero is within ERRREL.
Default: ERRREL = 1.e-4 for single precision and 1.d-8 for double precision.

MAXFN — On input, MAXFN specifies an upper bound on the number of function evaluations required for convergence. (Input/Output)
On output, MAXFN will contain the actual number of function evaluations used.
Default: MAXFN = 100.

FORTRAN 90 Interface

Generic: CALL ZBREN (F, A, B [,…])

Specific: The specific interface names are S_ZBREN and D_ZBREN.

FORTRAN 77 Interface

Single: CALL ZBREN (F, ERRABS, ERRREL, A, B, MAXFN)

Double: The double precision name is DZBREN.

Description

The algorithm used by ZBREN is a combination of linear interpolation, inverse quadratic interpolation, and bisection. Convergence is usually superlinear and is never much slower than the rate for the bisection method. See Brent (1971) for a more detailed account of this algorithm.

Comments

1. Informational error

Type Code

4 1 Failure to converge in MAXFN function evaluations.

2. On exit from ZBREN without any error message, A and B satisfy the following:

F(A)F(B) ≤ 0.0

|F(B)| ≤ |F(A)|, and

either |F(B)| ≤ ERRABS or

|A - B| ≤ max(|B|, 0.1) * ERRREL.

The presence of 0.1 in the stopping criterion causes leading zeros to the right of the decimal point to be counted as significant digits. Scaling may be required in order to accurately determine a zero of small magnitude.

3. ZBREN is guaranteed to convergence within K function evaluations, where
K = (ln((B - A)/D) + 1.0)2, and

This is an upper bound on the number of evaluations. Rarely does the actual number of evaluations used by ZBREN exceed

D can be computed as follows:
P = AMAX1(0.1, AMIN1(|A|, |B|))
IF((A - 0.1) * (B - 0.1) < 0.0) P = 0.1,
D = P * ERRREL

Example

This example finds a zero of the function

f(x) = x 2 + x - 2

in the interval ( - 10.0, 0.0).

USE ZBREN_INT

USE UMACH_INT

IMPLICIT NONE

! Declare variables

REAL ERRABS, ERRREL

INTEGER NOUT, MAXFN

REAL A, B, F

EXTERNAL F

! Set values of A, B, ERRABS,

! ERRREL, MAXFN

A = -10.0

B = 0.0

ERRABS = 0.0

ERRREL = 0.001

MAXFN = 100

CALL UMACH (2, NOUT)

! Find zero of F

CALL ZBREN (F, A, B, ERRABS=ERRABS, ERRREL=ERRREL, MAXFN=MAXFN)

WRITE (NOUT,99999) B, MAXFN

99999 FORMAT (' The best approximation to the zero of F is equal to', &

F5.1, '.', /, ' The number of function evaluations', &

' required was ', I2, '.', //)

END

REAL FUNCTION F (X)

REAL X

F = X**2 + X - 2.0

RETURN

END

Output

The best approximation to the zero of F is equal to -2.0.
The number of function evaluations required was 12.

Visual Numerics, Inc.
Visual Numerics - Developers of IMSL and PV-WAVE
http://www.vni.com/
PHONE: 713.784.3131
FAX:713.781.9260