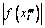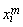Finds the real zeros of a real function using Müller's method.
Required Arguments
F — User-supplied FUNCTION to compute the value of the function of which a zero will be found. The form is F(X), where
X – The point at which
the function is evaluated. (Input)
X should not be
changed by F.
F – The computed
function value at the point X.
(Output)
F must be declared EXTERNAL in the
calling program.
X — A vector of
length NROOT.
(Output)
X contains the
computed zeros.
Optional Arguments
ERRABS — First
stopping criterion. (Input)
A zero X(I) is accepted if ABS(F(X(I)).LT. ERRABS.
Default: ERRABS = 1.e-4 for
single precision and 1.d-8 for double precision.
ERRREL — Second
stopping criterion is the relative error. (Input)
A zero X(I) is accepted if the
relative change of two successive approximations to X(I) is less than ERRREL.
Default: ERRREL = 1.e-4 for
single precision and 1.d-8 for double precision.
EPS — See ETA.
(Input)
Default: EPS = 1.e-4 for single
precision and 1.d-8 for double precision.
ETA — Spread
criteria for multiple zeros. (Input)
If the zero X(I) has been computed
and ABS(X(I) - X(J)).LT.EPS, where X(J) is a previously
computed zero, then the computation is restarted with a guess equal to
X(I) + ETA.
Default: ETA = .01.
NROOT — The
number of zeros to be found by ZREAL.
(Input)
Default: NROOT = 1.
ITMAX — The
maximum allowable number of iterations per zero. (Input)
Default:
ITMAX = 100.
XGUESS — A vector
of length NROOT.
(Input)
XGUESS contains the
initial guesses for the zeros.
Default: XGUESS = 0.0.
INFO — An integer
vector of length NROOT.
(Output)
INFO(J) contains the number
of iterations used in finding the J-th zero when
convergence was achieved. If convergence was not obtained in ITMAX iterations, INFO(J) will be greater
than ITMAX.
FORTRAN 90 Interface
Generic: CALL ZREAL (F, X [,…])
Specific: The specific interface names are S_ZREAL and D_ZREAL.
FORTRAN 77 Interface
Single: CALL ZREAL (F, ERRABS, ERRREL, EPS, ETA, NROOT, ITMAX, XGUESS, X, INFO)
Double: The double precision name is DZREAL.
Description
Routine ZREAL computes n real zeros of a real function f. Given a user-supplied function f(x) and an n-vector of initial guesses x1, x2, …, xn, the routine uses Müller's method to locate n real zeros of f, that is, n real values of x for which f(x) = 0. The routine has two convergence criteria: the first requires that
be less than ERRABS; the second requires that the relative change of any two successive approximations to an xi be less than ERRREL. Here,
is the m-th approximation to xi. Let ERRABS be ɛ1, and ERRREL be ɛ2.The criteria may be stated mathematically as follows:
“Convergence” is the satisfaction of either criterion.
Comments
3 1 Failure to converge within ITMAX iterations for at least one of the NROOT roots.
2. Routine ZREAL always returns the last approximation for zero J in X(J). If the convergence criterion is satisfied, then INFO(J) is less than or equal to ITMAX. If the convergence criterion is not satisfied, then INFO(J) is set to ITMAX + 1.
3. The routine ZREAL assumes that there exist NROOT distinct real zeros for the function F and that they can be reached from the initial guesses supplied. The routine is designed so that convergence to any single zero cannot be obtained from two different initial guesses.
4. Scaling the X vector in the function F may be required, if any of the zeros are known to be less than one.
Example
This example finds the real zeros of the second-degree polynomial
with the initial guess (4.6, -193.3).
REAL F, X(NROOT), XGUESS(NROOT)
CALL ZREAL (F, X, errabs=errabs, errrel=errrel, eps=eps, &
CALL WRRRN ('The zeros are', X, 1, NROOT, 1)
Output
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |