This function evaluates the derivative of the Kelvin function of the second kind, kei, of order zero.

Function Return Value

AKEIP0 — Function value.   (Output)

Required Arguments

X — Argument for which the function value is desired.   (Input)
It must be nonnegative.

FORTRAN 90 Interface

Generic:                              AKEIP0 (X)

Specific:                             The specific interface names are S_AKEIP0 and D_AKEIP0.

FORTRAN 77 Interface

Single:                                AKEIP0 (X)

Double:                              The double precision name is DKEIP0.

Description

The function keiʹ0(x) is defined to be

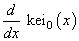
where kei0(x) is a Kelvin function, see AKEI0. Function AKEIP0 is based on the work of Burgoyne (1963).

If x < 0, then NaN (not a number) is returned. If x > 119, then zero is returned.

Example

In this example, keiʹ0(0.6) is computed and printed.

 

      USE AKEIP0_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

!                                 Declare variables

      INTEGER    NOUT

      REAL       VALUE, X, AKEIP0

!                                 Compute

      X     = 0.6

      VALUE = AKEIP0(X)

!                                 Print the results

      CALL UMACH (2, NOUT)

      WRITE (NOUT,99999) X, VALUE

99999 FORMAT (' AKEIP0(', F6.3, ') = ', F6.3)

      END

Output

 

AKEIP0( 0.600) = 0.348

http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260