This function evaluates the logarithmic integral.

Function Return Value

ALI — Function value.    (Output)

Required Arguments

X — Argument for which the logarithmic integral is desired.   (Input)
It must be greater than zero and not equal to one.

FORTRAN 90 Interface

Generic:                              ALI (X)

Specific:                             The specific interface names are S_ALI and D_ALI.

FORTRAN 77 Interface

Single:                                ALI (X)

Double:                              The double precision function name is DALI.

Description

The logarithmic integral, li(x), is defined to be

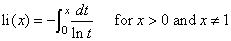
The argument x must be greater than zero and not equal to one. To avoid an undue loss of accuracy, x must be different from one at least by the square root of the machine precision.

The function li(x) approximates the function π(x), the number of primes less than or equal to x. Assuming the Riemann hypothesis (all non-real zeros of ζ(z) are on the line ℜz = 1/2), then

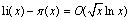
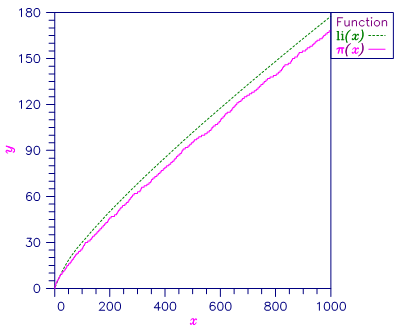
Figure 3- 2  Plot of li(x) and π(x)

Comments

Informational error

Type Code

3         2                  Result of ALI(X) is accurate to less than one-half precision because X is too close to 1.0.

Example

In this example, li(2.3) is computed and printed.

 

      USE ALI_INT

      USE UMACH_INT

 

      IMPLICIT   NONE

!                                 Declare variables

      INTEGER    NOUT

      REAL       VALUE, X

!                                 Compute

      X     = 2.3

      VALUE = ALI(X)

!                                 Print the results

      CALL UMACH (2, NOUT)

      WRITE (NOUT,99999) X, VALUE

99999 FORMAT (' ALI(', F6.3, ') = ', F6.3)

      END

Output

 

ALI( 2.300) =  1.439

http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260