Evaluates the exponential integral of integer order for arguments greater than zero scaled by EXP(X).
Required Arguments
X — Argument for
which the integral is to be evaluated. (Input)
It must be
greater than zero.
N — Integer specifying the maximum order for which the exponential integral is to be calculated. (Input)
F — Vector of length N containing the computed exponential integrals scaled by EXP(X). (Output)
FORTRAN 90 Interface
Generic: CALL ENE (X, N, F)
Specific: The specific interface names are S_ENE and D_ENE.
FORTRAN 77 Interface
Single: CALL ENE (X, N, F)
Double: The double precision function name is DENE.
Description
The scaled exponential integral of order n, En(x), is defined to be
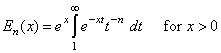
The argument x must satisfy x > 0. The integer n must also be greater than zero. This code is based on a code due to Gautschi (1974).
Example
In this example, Ez(10) for n = 1, ..., n is computed and printed.
USE ENE_INT
USE UMACH_INT
IMPLICIT NONE
! Declare variables
INTEGER N
PARAMETER (N=10)
!
INTEGER K, NOUT
REAL F(N), X
! Compute
X = 10.0
CALL ENE (X, N, F)
! Print the results
CALL UMACH (2, NOUT)
DO 10 K=1, N
WRITE (NOUT,99999) K, X, F(K)
10 CONTINUE
99999 FORMAT (' E sub ', I2, ' (', F6.3, ') = ', F6.3)
END
Output
E sub 1 (10.000) = 0.092
E sub 2 (10.000) = 0.084
E sub 3 (10.000) = 0.078
E sub 4 (10.000) = 0.073
E sub 5 (10.000) = 0.068
E sub 6 (10.000) = 0.064
E sub 7 (10.000) = 0.060
E sub 8 (10.000) = 0.057
E sub 9 (10.000) = 0.054
E sub 10 (10.000) = 0.051
|
PHONE: 713.784.3131 FAX:713.781.9260 |