This function evaluates the noncentral beta probability density function.
Function Return Value
BETNPR — Function value, the value of the probability density function. (Output)
Required Arguments
X — Argument for
which the noncentral beta probability density function is to be
evaluated. (Input)
X must be non-negative and less than or equal to
1.
SHAPE1 — First
shape parameter of the noncentral beta distribution.
(Input)
SHAPE1 must be positive.
SHAPE2 — Second
shape parameter of the noncentral beta distribution.
(Input)
SHAPE2 must be positive.
LAMBDA —
Noncentrality parameter. (Input)
LAMBDA must be non-negative.
FORTRAN 90 Interface
Generic: BETNPR (X, SHAPE1, SHAPE2, LAMBDA)
Specific: The specific interface names are S_BETNPR and D_BETNPR.
Description
The noncentral beta distribution is a generalization of the
beta distribution. If Z is a noncentral chi-square random variable
with noncentrality parameter 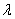 and
and 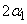 degrees
of freedom, and Y is a chi-square random variable with
degrees
of freedom, and Y is a chi-square random variable with 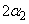 degrees
of freedom which is statistically independent of Z, then
degrees
of freedom which is statistically independent of Z, then
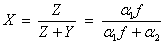
is a noncentral beta-distributed random variable and
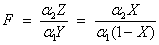
is a noncentral F-distributed random variable. The PDF for noncentral beta variable X can thus be simply defined in terms of the noncentral F PDF:
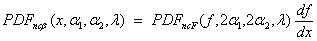
Where 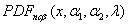 is a noncentral beta PDF with
is a noncentral beta PDF with
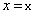 ,
, 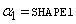 ,
, 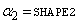 , and noncentrality parameter
, and noncentrality parameter
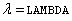 ;
; 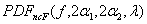 is a noncentral F PDF with argument f , numerator
and denominator degrees of freedom
is a noncentral F PDF with argument f , numerator
and denominator degrees of freedom 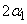 and
and
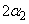 respectively, and
noncentrality parameter
respectively, and
noncentrality parameter 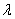 ; and:
; and:
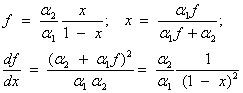
(See the documentation for function FNPR for a discussion of how the noncentral F PDF is defined and calculated.)
With a noncentrality parameter of zero, the noncentral beta distribution is the same as the beta distribution.
Example
This example traces out a portion of a noncentral beta distribution with parameters SHAPE1 = 50, SHAPE2 = 5, and LAMBDA = 10.
USE UMACH_INT
USE BETNPR_INT
USE FNPR_INT
IMPLICIT NONE
INTEGER NOUT, I
REAL X, LAMBDA, SHAPE1, SHAPE2, &
BPDFV, FPDFV, DBETNPR, DFNPR, F(8), &
BPDFVEXPECT, DFDX
DATA F /0.0, 0.4, 0.8, 3.2, 5.6, 8.8, 14.0, 18.0/
CALL UMACH (2, NOUT)
SHAPE1 = 50.0
SHAPE2 = 5.0
LAMBDA = 10.0
WRITE (NOUT,'(/" SHAPE1: ", F4.0, "; SHAPE2: ", F4.0, "; '// &
'LAMBDA: ", F4.0 // 6x,"X",6x,"NCBETPDF(X)",3x,"NCBETPDF'// &
'(X)",/ 14x,"expected")') SHAPE1, SHAPE2, LAMBDA
DO I = 1, 8
X = (SHAPE1*F(I)) / (SHAPE1*F(I) + SHAPE2)
DFDX = (SHAPE2/SHAPE1) / (1.0 - X)**2
FPDFV = FNPR(F(I),2*SHAPE1,2*SHAPE2,LAMBDA)
BPDFVEXPECT = DFDX * FPDFV
BPDFV = BETNPR(X, SHAPE1, SHAPE2, LAMBDA)
WRITE (NOUT,'(2X, F8.6, 2(2X, E12.6))') X, BPDFVEXPECT, BPDFV
END DO
END
Output
SHAPE1: 50.; SHAPE2: 5.; LAMBDA: 10.
X NCBETPDF(X) NCBETPDF(X)
expected
0.000000 0.000000E+00 0.000000E+00
0.800000 0.243720E+00 0.243720E+00
0.888889 0.658624E+01 0.658624E+01
0.969697 0.402367E+01 0.402365E+01
0.982456 0.919544E+00 0.919542E+00
0.988764 0.219100E+00 0.219100E+00
0.992908 0.436654E-01 0.436647E-01
0.994475 0.175215E-01 0.175217E-01
|
PHONE: 713.784.3131 FAX:713.781.9260 |