This function evaluates the inverse of the noncentral beta cumulative distribution function (CDF).
Function Return Value
BETNIN — Function value, the value of the inverse of the cumulative distribution function evaluated at P. The probability that a noncentral beta random variable takes a value less than or equal to BETNIN is P. (Output)
Required Arguments
P — Probability
for which the inverse of the noncentral beta cumulative distribution function is
to be evaluated. (Input)
P must be non-negative
and less than or equal to 1.
SHAPE1 — First
shape parameter of the noncentral beta distribution.
(Input)
SHAPE1 must be positive.
SHAPE2 — Second
shape parameter of the noncentral beta distribution.
(Input)
SHAPE2 must be positive.
LAMBDA —
Noncentrality parameter. (Input)
LAMBDA must be non-negative.
FORTRAN 90 Interface
Generic: BETNIN (P, SHAPE1, SHAPE2, LAMBDA)
Specific: The specific interface names are S_BETNIN and D_BETNIN.
Description
The noncentral beta distribution is a generalization of the
beta distribution. If 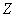 is a noncentral chi-square random variable with
noncentrality parameter
is a noncentral chi-square random variable with
noncentrality parameter 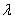 and
and  degrees
of freedom, and
degrees
of freedom, and 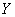 is a chi-square random
variable with
is a chi-square random
variable with  degrees of freedom which is
statistically independent of
degrees of freedom which is
statistically independent of 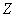 , then
, then
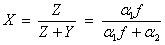
is a noncentral beta-distributed random variable and
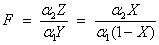
is a noncentral F-distributed random variable.
The CDF for noncentral beta variable 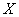 can thus be simply defined in terms of the noncentral
F CDF:
can thus be simply defined in terms of the noncentral
F CDF:

where 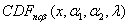 is a noncentral beta
CDF with
is a noncentral beta
CDF with 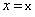 ,
, 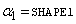 ,
, 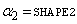 , and noncentrality parameter
, and noncentrality parameter
 ;
; 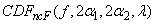 is a noncentral F CDF with argument f ,
numerator and denominator degrees of freedom
is a noncentral F CDF with argument f ,
numerator and denominator degrees of freedom  and
and
 respectively, and
noncentrality parameter
respectively, and
noncentrality parameter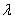 ;
; 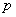 = the probability that
= the probability that
 = the probability that
= the probability that 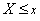 and:
and:

(See the documentation for function FNDF for a discussion of how the noncentral
F CDF is defined and calculated.) The correspondence between the
arguments of function BETNIN(P,SHAPE1,SHAPE2,LAMBDA) and the variables in the above equations is as follows:
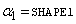 ,
,
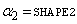 ,
,
 ,
and p = P.
,
and p = P.
Function BETNIN evaluates
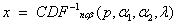
by first evaluating
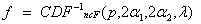
and then solving for x using
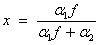
(See the documentation for function FNIN for a discussion of how the inverse noncentral F CDF is calculated.)
Example
This example traces out a
portion of an inverse noncentral beta distribution with parameters
SHAPE1 = 50, SHAPE2 = 5, and LAMBDA = 10.
USE UMACH_INT
USE BETNDF_INT
USE BETNIN_INT
USE UMACH_INT
IMPLICIT NONE
INTEGER :: NOUT, I
REAL :: SHAPE1 = 50.0, SHAPE2=5.0, LAMBDA=10.0
REAL :: X, CDF, CDFINV
REAL :: F0(8)=(/ 0.0, .4, .8, 1.2, 1.6, 2.0, 2.8, 4.0 /)
CALL UMACH (2, NOUT)
WRITE (NOUT,'(/" SHAPE1: ", F4.0, " SHAPE2: ", F4.0,'// &
'" LAMBDA: ", F4.0 // ' // &
'" X P = CDF(X) CDFINV(P)")') &
SHAPE1, SHAPE2, LAMBDA
DO I = 1, 8
X = (SHAPE1*F0(I))/(SHAPE2 + SHAPE1*F0(I))
CDF = BETNDF(X, SHAPE1, SHAPE2, LAMBDA)
CDFINV = BETNIN(CDF, SHAPE1, SHAPE2, LAMBDA)
WRITE (NOUT,'(3(2X, E12.6))') X, CDF, CDFINV
END DO
END
Output
SHAPE1: 50. SHAPE2: 5. LAMBDA: 10.
X P = CDF(X) CDFINV(P)
0.000000E+00 0.000000E+00 0.000000E+00
0.800000E+00 0.488791E-02 0.800000E+00
0.888889E+00 0.202633E+00 0.888889E+00
0.923077E+00 0.521144E+00 0.923077E+00
0.941176E+00 0.733853E+00 0.941176E+00
0.952381E+00 0.850413E+00 0.952381E+00
0.965517E+00 0.947125E+00 0.965517E+00
0.975610E+00 0.985358E+00 0.975610E+00
|
PHONE: 713.784.3131 FAX:713.781.9260 |