This function evaluates the Airy function of the second kind.
Function Return Value
BI — Function value. (Output)
Required Arguments
X — Argument for which the Airy function value is desired. (Input)
FORTRAN 90 Interface
Generic: BI (X)
Specific: The specific interface names are S_BI and D_BI.
FORTRAN 77 Interface
Single: BI (X)
Double: The double precision name is DBI.
Description
The Airy function of the second kind Bi(x) is defined to be
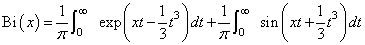
It can also be expressed in terms of modified Bessel functions of the first kind, Iν (x), and Bessel functions of the first kind, Jν(x) (see BSIS and BSJS):
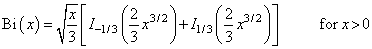
and
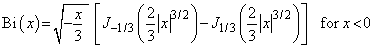
Let ε = AMACH(4),
the machine precision. If 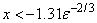 , then the answer will have
no precision. If
, then the answer will have
no precision. If 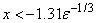 , the answer will be less
accurate than half precision. In addition, x should not be so large that
, the answer will be less
accurate than half precision. In addition, x should not be so large that
 overflows. If overflows
are a problem, consider using the exponentially scaled form of the Airy function
of the second kind, BIE, instead.
overflows. If overflows
are a problem, consider using the exponentially scaled form of the Airy function
of the second kind, BIE, instead.
Example
In this example, Bi(−4.9) is computed and printed.
USE BI_INT
USE UMACH_INT
IMPLICIT NONE
! Declare variables
INTEGER NOUT
REAL VALUE, X
! Compute
X = -4.9
VALUE = BI(X)
! Print the results
CALL UMACH (2, NOUT)
WRITE (NOUT,99999) X, VALUE
99999 FORMAT (' BI(', F6.3, ') = ', F6.3)
END
Output
BI(-4.900) = -0.058
|
PHONE: 713.784.3131 FAX:713.781.9260 |